0,999...

0,999...

Representació gràfica de la infinitud dels seus decimals
Tipus	nombre natural i Nombre decimal periòdic
Propietats
Valor	1
Altres numeracions
Numeral romà	I
Binari	12
Hexadecimal	116

En matemàtiques, el nombre 0,999… amb el 9 com un nombre decimal periòdic, denota el nombre natural u. En altres paraules, les notacions «0,999…» i «1» representen el mateix nombre en el sistema de nombres reals. Les demostracions d'aquesta igualtat s'han formulat amb diversos graus de rigor matemàtic, tot depenent del mètode preferit per definir els nombres reals, les hipòtesis i suposicions de partida, el context històric i l'audiència d'objectiu.

Certs nombres reals es poden representar per més d'una cadena de dígits i aquest fet no és un cas que es limiti al sistema decimal. El mateix fenomen succeeix en totes les bases d'enters, i els matemàtics també han quantificat les formes per escriure 1 en bases no enteres. Aquest tampoc no és un fenomen únic de l'1: tots els nombres diferents de zero amb una representació decimal finita tenen un bessó periòdic pur acabat en xifres decimals iguals a 9, com 28,3287 i 28,3286999… Per a simplificar-ho, el decimal finit és gairebé sempre la representació preferida, contribuint a una mala interpretació el fet que sigui l'única representació. Fins i tot de manera més general, qualsevol sistema de numeració posicional conté una quantitat infinita de nombres amb representacions múltiples. Aquestes diverses identitats s'han aplicat d'aquesta manera per entendre més bé els patrons en les expansions decimals de fraccions i l'estructura d'un fractal simple, el conjunt de Cantor. També apareixen en la investigació ja clàssica de la infinitat del conjunt sencer dels nombres reals.

La igualtat $0,999...=1$ ha estat acceptada durant molt de temps pels matemàtics professionals i s'ha ensenyat en els llibres de text. En les darreres dècades, els experts en l'ensenyament de matemàtiques han estudiat la percepció d'aquesta igualtat entre els estudiants, molts dels quals inicialment qüestionen o rebutgen aquesta igualtat. Molts es basen en una apel·lació a l'autoritat d'acord amb determinats llibres de text i professors, o per raonaments aritmètics com els de no acceptar que tots dos siguin iguals. Tanmateix, alguns sovint se senten prou molestos per buscar una altra justificació. El raonament dels estudiants per negar o afirmar la igualtat es basa típicament en un error —d'entre uns quants errors comuns—, provocat pel comportament contrari a la intuïció dels nombres reals. Per exemple, que cada nombre real té una expansió decimal única, que els nombres reals infinitesimals diferents de zero haurien d'existir, o que l'expansió de 0,999… finalment acaba.

Es poden construir sistemes de nombres que compleixin algunes d'aquestes intuïcions, i en alguns d'aquests sistemes la igualtat és falsa. Cal considerar que aquests sistemes de nombres són diferents del sistema de nombres reals estàndard que es fa servir en matemàtica elemental, i que ja s'ha comentat. En efecte, algunes construccions de nombres contenen nombres que són "infinitesimalment" propers a 1; generalment no estan relacionats amb 0,999…, però són d'interès considerable en anàlisi matemàtica.

Consideracions prèvies

0,999… és un nombre escrit en el sistema de numeració decimal, i algunes de les proves més senzilles que afirmen que $0,999...=1$ es basen en les propietats aritmètiques d'aquest sistema. La majoria d'operacions de suma, resta, multiplicació, divisió, i manipulacions de comparació fan servir algun tipus de manipulació pel que fa a dígits que són molt semblants a les que es fan amb nombres enters. Com en el cas dels enters, dos decimals qualsevol finits amb dígits diferents signifiquen nombres diferents, sempre ignorant els zeros de la dreta. En particular, qualsevol nombre de la forma 0,99…9, on les xifres 9 finalment s'aturen, és estrictament menor que 1.

Malinterpretar el significat de l'ús dels "…" (punts suspensius) en l'expressió numèrica 0,999… genera un malentès amb relació a la seva igualtat a 1. L'ús, aquí, és diferent del que es fa servir en la llengua o en l'expressió 0,99…9, on els punts suspensius especifiquen que una porció aproximadament «finita» es deixa sense manifestar o és omesa. Quan "…" es fa servir per especificar un decimal periòdic, vol dir que una porció «infinita» s'ha deixat sense manifestar; aquesta afirmació només es pot interpretar com un nombre fent servir el concepte matemàtic de límits. Com a resultat, en l'ús matemàtic convencional el valor assignat a la notació "0,999…" es defineix com el nombre real que és el límit de la successió convergent (0,9; 0,99; 0,999; 0,9999; etc.).

A diferència del que succeeix amb els enters i els decimals finits, notacions diferents també poden expressar de maneres múltiples un únic nombre. Com, per exemple, fent servir fraccions ¹⁄₃ = ²⁄₆. Els decimals infinits, tanmateix, poden expressar el mateix nombre com a màxim de dues maneres diferents. Si hi ha dues maneres, llavors una d'elles ha d'acabar amb una sèrie infinita de xifres 9, i l'altra consta d'una sèrie de zeros que es repeteixen a partir d'un cert punt.

Hi ha moltes demostracions que conclouen que 0,999… = 1, amb diversos graus de rigor matemàtic. Un breu esbós d'una prova rigorosa es pot expressar simplement de la manera següent: considereu que dos nombres reals siguin idèntics si i només si la seva diferència és igual a zero. La majoria de les persones acceptarien que la diferència entre 0,999… i 1, si és que existeix, ha de ser molt petita. Considerant la convergència de la seqüència de dalt, es pot demostrar que la magnitud d'aquesta diferència ha de ser més petita que qualsevol quantitat positiva, i es pot demostrar que l'únic nombre real amb aquesta propietat és el 0. Com la diferència és 0 es pot concloure que els nombres 1 i 0,999… són idèntics. El mateix argument també explica per què 0,333… = ¹⁄₃, 0,111… = ¹⁄₉, etc.

Demostracions

Algebraiques

Fraccions i divisió euclidiana

Una raó per la qual els decimals infinits són una ampliació necessària dels decimals finits és que serveixen per representar fraccions. Utilitzant l'algorisme de dividir, una divisió simple d'enters com ¹⁄₃ esdevé un decimal periòdic, 0,333…, en el qual els dígits es repeteixen sens fi. Aquest decimal produeix una demostració ràpida del tipus $0,999...=1$. La multiplicació de 3 per 3 dona 9 a cada dígit; així, $3\times 0,333...=0,999...$. I també $3\times {\frac {1}{3}}=1$; d'aquesta manera $0,999...=1$.

Una altra forma d'aquesta prova multiplica ${\frac {1}{9}}=0,111...$ per 9.

${\begin{aligned}0,333\dots &{}={\frac {1}{3}}\\3\times 0,333\dots &{}=3\times {\frac {1}{3}}={\frac {3\times 1}{3}}\\0,999\dots &{}=1\end{aligned}}$

${\begin{aligned}0,111\dots &{}={\frac {1}{9}}\\9\times 0,111\dots &{}=9\times {\frac {1}{9}}={\frac {9\times 1}{9}}\\0,999\dots &{}=1\end{aligned}}$

Una versió més compacta de la mateixa prova ve donada per les equacions següents:

$1={\frac {9}{9}}=9\times {\frac {1}{9}}=9\times 0,111\dots =0,999\dots$

Ja que les dues equacions són vàlides, 0,999… s'ha d'igualar a 1 (per la propietat transitiva). De manera similar ${\frac {3}{3}}=1$, i ${\frac {3}{3}}=0,999...$. Així 0,999… s'ha d'igualar a 1.

Manipulació de dígits

Hi ha una altra classe de prova que s'adapta més fàcilment a altres decimals que es repeteixen. Quan un nombre en notació decimal es multiplica per 10, els dígits no canvien però el separador decimal es desplaça un lloc a la dreta. Així, «10 × 0,999… = 9,999…» i el resultat és nou unitats més gran que el nombre original.

Per veure-ho, es resta 0,999… de 9,999… i es pot continuar dígit a dígit; en cada un dels dígits després del separador decimal el resultat és «9 − 9», que dona com a resultat 0. Però afegint zeros a la dreta de la coma no modifica un nombre i, per tant, la diferència és exactament 9. El pas final fa servir operacions d'àlgebra. Sia el nombre decimal en qüestió (0,999…) al que anomenem x; llavors «10x − x = 9». Això és el mateix que «9x = 9». Dividint els dos costats entre 9 completa la prova: «x = 1». Tot això, escrit com una seqüència d'equacions es presenta:

${\begin{aligned}x&=0,999\ldots \\10x&=9,999\ldots \\10x-x&=9,999\ldots -0,999\ldots \\9x&=9\\x&=1\\0,999\ldots &=1\end{aligned}}$

La validesa de les manipulacions de dígits de les dues proves anteriors no s'han d'acceptar per una qüestió de fe o com un axioma; deriven de la relació fonamental entre els decimals i els nombres que representen. Aquesta relació, que es pot desenvolupar d'unes quantes maneres equivalents, ja estableix que els decimals 0,999… i 1,000… representen el mateix nombre.

Analítica

Com que la qüestió de 0,999… no afecta el desenvolupament formal de les matemàtiques, es pot ajornar fins que es demostrin els teoremes estàndards de l'anàlisi real. Uns requisits necessaris són caracteritzar els nombres reals que es poden escriure en notació decimal —que està compost per un signe opcional—, en una seqüència finita de qualsevol nombre de dígits que formen una part entera, en un separador decimal, i en una seqüència de dígits que formen una part fraccionària. Per tal de parlar de 0,999… la part entera es pot resumir com b₀ i es poden negligir els negatius. D'aquesta manera una expansió decimal té la forma

$b_{0}.b_{1}b_{2}b_{3}b_{4}b_{5}\dots$

És vital que la part fraccionària, a diferència de la part entera, no estigui limitada a un nombre finit de dígits; això és una notació posicional. D'aquesta manera, per exemple, el 5 en 500 contribueix amb deu vegades més que el 5 en 50, i el 5 en 0,05 contribueix amb una desena part com el 5 en 0,5.

Sèrie Infinita i successions

El desenvolupament d'expansions decimals més habitual és, probablement, el de definir-les com a sumes de sèries infinites. En general:

$b_{0}.b_{1}b_{2}b_{3}b_{4}\ldots =b_{0}+b_{1}\left({\tfrac {1}{10}}\right)+b_{2}\left({\tfrac {1}{10}}\right)^{2}+b_{3}\left({\tfrac {1}{10}}\right)^{3}+b_{4}\left({\tfrac {1}{10}}\right)^{4}+\cdots .$

Per a 0,999… es pot aplicar el teorema de convergència pel que fa a la sèrie geomètrica:

Si $|r|<1\,\!$ llavors $ar+ar^{2}+ar^{3}+\cdots ={\frac {ar}{1-r}}.$

Com que 0,999… és una suma donada amb una raó comuna $r=\textstyle {\frac {1}{10}}$, el teorema resol la qüestió:

$0,999\ldots =9\left({\tfrac {1}{10}}\right)+9\left({\tfrac {1}{10}}\right)^{2}+9\left({\tfrac {1}{10}}\right)^{3}+\cdots ={\frac {9\left({\tfrac {1}{10}}\right)}{1-{\tfrac {1}{10}}}}=1.\,$

Aquesta demostració (de fet, que 10 és igual a 9,999…) apareix ja l'any 1770 als Elements d'àlgebra de Leonhard Euler.

Exemple de límits. L'interval unitat, incloent-hi la successió decimal en base 4 (0,3; 0,33; 0,333; …) convergint a 1.

La suma d'una sèrie geomètrica és un resultat fins i tot més antic que el d'Euler. Una demostració típica del segle xviii fa servir una manipulació terme-a-terme similar a la demostració emprant l'àlgebra donada anteriorment. També el 1811, el llibre de text de John Bonnycastle, Una introducció a l'àlgebra, fa servir una sèrie geomètrica com aquesta per justificar la mateixa maniobra en el cas de 0,999… Una reacció a tals mètodes d'addició liberals produïda al segle xix portà com a conseqüència la definició que encara domina avui: la suma d'una sèrie es defineix com el límit de la successió de les seves sumes parcials. Una demostració corresponent del teorema calcula explícitament aquesta successió; es pot trobar en qualsevol introducció al càlcul o l'anàlisi basada en la demostració.

Una successió (x₀, x₁, x₂, …) té un límit x si la distància |x − x_n| esdevé arbitràriament petita a mesura que n augmenta. La mateixa afirmació 0,999… = 1 es pot interpretar i demostrar com un límit:.

$0,999\ldots =\lim _{n\to \infty }0,\underbrace {99\ldots 9} _{n}=\lim _{n\to \infty }\sum _{k=1}^{n}{\frac {9}{10^{k}}}=\lim _{n\to \infty }\left(1-{\frac {1}{10^{n}}}\right)=1-\lim _{n\to \infty }{\frac {1}{10^{n}}}=1.\,$

L'últim pas

$\lim _{n\to \infty }{\frac {1}{10^{n}}}=0$

sovint es justifica per l'axioma que els nombres reals tenen la propietat arquimediana. Aquesta actitud basada en el límit cap a 0,999… sovint s'explica en més termes evocatius, però menys precisos. Per exemple, a Aritmètica d'Universitat, un llibre de text de 1846, s'explica: «0,999 +, continuat a l'infinit = 1, perquè totes les annexions d'un 9 porten el valor més proper a 1.» Mig segle més tard (1895), a Aritmètica per a Escoles, es diu: «... quan es pren un nombre gran de 9 segons, la diferència entre 1 i 0,99999… esdevé inconcebiblement petita"» Aquestes heurístiques són sovint interpretades pels estudiants en el sentit que impliquen que 0,999… mateix és menor que 1.

Intervals niats i ínfims

Intervals niats: en base 3, 1 = 1,000… = 0,222…

La definició de la secció anterior que utilitza sèries és una manera senzilla de definir un nombre real descrit per una expressió decimal periòdica. Un enfocament complementari segueix el procés oposat: per a un determinat nombre real, cal definir l'expansió o expansions decimals per anomenar-lo.

Si un nombre real x pertany a l'interval tancat [0, 10] (és a dir, és "més gran o igual a 0" i "més petit o igual a 10"), es pot imaginar de dividir aquell interval en deu peces que s'encavalquin només en els seus punts finals: [0, 1], [1, 2], [2, 3], etcètera fins a [9, 10]. El nombre x ha de pertànyer a un d'ells; si pertany a [2, 3] llavors s'enregistra el dígit "2" i se subdivideix aquell interval en [2, 2.1], [2.1, 2.2], …;, [2.8, 2.9], [2.9, 3]. Continuant aquest procés es produeix una successió infinita d'intervals niats, etiquetada per una successió infinita de dígits b₀, b₁, b₂, b₃, …, i s'escriu:

x = b₀.b₁b₂b₃…

En aquest formalisme, les identitats $1=0,999...$ i $1=1.000...$ reflecteixen, respectivament, el fet que 1 sigui en els dos intervals [0, 1] i [1, 2]; d'aquesta manera es pot escollir qualsevol subinterval en què es poden trobar els seus dígits. Per assegurar que aquesta notació no abusi del signe "=", cal un camí que reconstrueixi un nombre real únic per a cada decimal. Això es pot fer amb límits, però altres construccions donen continuïtat al tema de l'ordenació.

L'elecció directa és el teorema d'intervals niats que garanteix que donada una successió d'intervals tancats niats, les llargades del qual es tornen arbitràriament petites, els intervals contenen exactament un nombre real en la seva intersecció. Així b₀.b₁b₂b₃… es defineix com l'únic nombre que està contingut dins de tots els intervals [b₀, b₀ + 1], [b₀.b₁, b ₀.b₁ + 0.1], etc. Llavors, 0,999… és el nombre real únic que apareix en tots els intervals [0, 1], [0,9, 1], [0,99, 1], i [0,99…9, 1] per a cada cadena finita de xifres 9. Com que 1 és un element de cada un d'aquests intervals, llavors $0,999...=1$.

El teorema dels Intervals Niats es basa normalment a una característica més fonamental dels nombres reals: l'existència de suprem o la més petita de les fites superiors. Per explotar directament aquests objectes, es pot definir b₀.b₁b₂b₃… com la fita superior més petita del conjunt d'aproximants {b₀, b₀.b₁, b₀.b₁b₂, …}. Llavors es pot mostrar que aquesta definició (o la definició d'intervals niats) és coherent amb el procediment de subdivisió, implicant 0,999… = 1 una altra vegada. Tom Apostol conclou:

El fet que un nombre real pugui tenir dues representacions decimals diferents és merament un reflex del fet que dos conjunts diferents de nombres reals puguin tenir el mateix suprem.

Basades en la construcció dels nombres reals

Vegeu també: Construcció dels nombres reals

Alguns enfocaments defineixen explícitament els nombres reals com certes estructures construïdes a partir dels nombres racionals, fent servir la teoria axiomàtica de conjunts. Els nombres naturals –0, 1, 2, 3, etc.– comencen amb el 0 i van pujant, de manera que tots els nombres tenen un successor. Es pot estendre els nombres naturals amb els seus negatius per obtenir tots els enters, i continuar estenent-los a proporcions, donant els nombres racionals. Aquests sistemes de nombres van acompanyats de les operacions aritmètiques d'addició, sostracció, multiplicació, i divisió. Més subtilment, inclouen l'ordenació, de manera que un nombre es pugui comparar amb un altre i trobar si és "més petit que", "més gran que", o "igual que" un altre nombre.

El pas des dels nombres racionals als reals és una ampliació essencial. Hi ha com a mínim dues maneres populars d'aconseguir aquest pas, les dues publicades l'any 1872: els Talls de Dedekind i les Successions de Cauchy. Als llibres de text sobre anàlisi real no es troben demostracions de $0,999...=1$ que directament utilitzin aquestes dues construccions; la tendència moderna durant les darreres dècades ha estat fer servir una anàlisi axiomàtica. Fins i tot quan s'ofereix una construcció, normalment s'aplica per demostrar els axiomes dels nombres reals, que llavors donen suport a les demostracions citades. Tanmateix, diversos autors creuen que començar a partir d'una construcció, des d'una perspectiva lògica és una forma més apropiada i les demostracions que en resulten són més autònomes.

Talls de Dedekind

Vegeu també: Talls de Dedekind

En l'enfocament basat en els talls de Dedekind, cada nombre real x es defineix com el conjunt infinit de tots els nombres racionals que són més petits que x. En particular, el nombre real 1 és el conjunt de tots els nombres racionals que són inferiors a 1. Cada expansió decimal positiva determina fàcilment un tall de Dedekind: el conjunt de nombres racionals que són menors que alguna etapa de l'expansió. Així el nombre real 0,999… és el conjunt de nombres racionals r tals que r < 0, o r < 0,9, o r < 0,99 o r és menor que algun altre nombre de la forma ${\begin{aligned}1-\left({\tfrac {1}{10}}\right)^{n}\end{aligned}}$. Tots els elements de 0,999… són menors que 1; per tant, és un element del nombre real 1. De manera recíproca, un element d'1 és un nombre racional: ${\begin{aligned}{\tfrac {a}{b}}<1\end{aligned}}$, que implica ${\begin{aligned}{\tfrac {a}{b}}<1-\left({\tfrac {1}{10}}\right)^{b}\end{aligned}}$. 0,999… i 1 contenen els mateixos nombres racionals; són el mateix: $0,999...=1$.

La definició de nombres reals com a Tall de Dedekind va ser publicada per primera vegada per Richard Dedekind l'any 1872.

Aquest enfocament que assigna un nombre real a cada expansió decimal va aparèixer en un article de Fred Richman titulat "És 0,999 … = 1?", adreçada a professors de matemàtiques d'escola, especialment dels nivells júnior i superior, i als seus estudiants. Richman observa que agafant talls de Dedekind en qualsevol subconjunt dens dels nombres racionals es produeixen els mateixos resultats. En particular, fa servir fraccions decimals, per a les quals la demostració és més immediata: «Així es veu que en la definició tradicional dels nombres reals, l'equació $0,9*=1$ s'incorpora al començament.» Una altra modificació del procediment condueix a una estructura diferent que Richman està més interessat a descriure; vegeu "sistemes de nombres alternatius" en una secció posterior.

Successions de Cauchy

Vegeu també: Successió de Cauchy

Un altre enfocament per construir els nombres reals fa servir l'ordenació dels racionals d'una manera menys directa. Primer de tot, la distància entre x i y es defineix com el valor absolut |x − y|, on el valor absolut |z| es defineix com el màxim de z i −z; d'aquesta manera mai és negatiu. A continuació, els nombres reals es defineixen com les successions de racionals que tenen la propietat de la successió de Cauchy, que fa servir aquesta distància. És a dir, en la successió (x₀, x₁, x₂, …), existeix una correspondència dels nombres naturals amb els racionals, per a qualsevol δ racional positiu; hi ha un N tal que |x_m − x_n| ≤ δ; per a tots m, n > N. La distància entre termes es torna més petita que qualsevol positiu racional.

Si (x_n ) i (y_n ) són dues seqüències de Cauchy, per ser iguals als nombres reals es defineixen d'acord amb si la seqüència (x_n − y_n ) té el límit 0. Els truncaments del nombre decimal b₀.b₁b₂b₃… generen una seqüència de racionals que és de Cauchy; es considera que aquest fet defineix el valor real del nombre. Així, en aquest formalisme, la tasca és demostrar que la seqüència de nombres racionals

$\left(1-0,1-{9 \over 10},1-{99 \over 100},\dots \right)=\left(1,{1 \over 10},{1 \over 100},\dots \right)$

té el límit 0. Considerant el terme número n de la seqüència, per $''n''=0,1,2,...$ per tant, cal demostrar que

$\lim _{n\rightarrow \infty }{\frac {1}{10^{n}}}=0.$

Aquest límit és clar; una prova possible és que per a ε = a / b > 0, en la definició del límit d'una seqüència es pot prendre un $''N''=''b''$. Per tant, una altra vegada $0,999...=1$.

La definició de nombres reals com a seqüències de Cauchy va ser publicada per primera vegada per Eduard Heine i Georg Cantor, per separat, també el 1872. L'aproximació a expansions decimals ja comentada, que inclou la prova de $0,999...=1$, segueix de prop l'obra de Griffiths i Hilton (1970), un llibre escrit específicament per oferir un segon punt de vista a diversos conceptes familiars, però des d'una perspectiva més actual.

Generalitzacions

El resultat $0,999...=1$ es generalitza immediatament de dues maneres:

1. Tots els nombres diferents de zero amb una notació decimal finita (o de manera equivalent, amb una notació que té infinits zeros a la dreta d'una determinada xifra després de la coma decimal) té un homòleg amb infinites xifres 9 a la dreta d'una determinada xifra després de la coma decimal. Per exemple: 0,24999… és igual a 0,25, exactament com en el cas especial que s'ha considerat. Aquests nombres són les fraccions decimals i són densos.
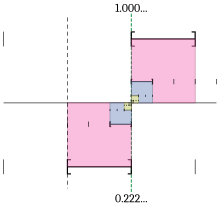
2. Un teorema comparable s'aplica en cada base. Per exemple, en base 2 (el nombre binari) 0,111… és igual a 1, i en base 3, el codi 0,222… és igual a 1. És probable que els llibres de text d'anàlisi real se saltin l'exemple de 0,999… i presentin una o aquestes dues generalitzacions des del començament.

Les representacions alternatives d'1 també succeeixen en bases no-enteres. Per exemple, en la base de la proporció àuria, les dues representacions estàndards són 1,000… i 0,101010…, i hi ha una quantitat infinita de representacions que n'inclouen d'adjacents. En general, per a gairebé tot q entre 1 i 2, hi ha una quantitat no numerable base-q d'expansions d'1. D'altra banda, hi ha encara una quantitat no numerable de bases-q (incloent-hi tots els nombres naturals més grans que 1) per a les quals només hi ha una expansió decimal base-q d'1, diferent de la trivial 1,000… Aquest resultat el va obtenir primer Paul Erdős, Miklos Horváth, i István Joó cap al 1990. L'any 1998 Vilmos Komornik i Paola Loreti determinaren la base més petita de totes, la constant de komornik-loreti $''q''=1.787231650...$. En aquesta base, $1=0.11010011001011010010110011010011...$, els dígits són definits per la successió de Thue–Morse, que no repeteix.

Una generalització d'un abast més gran encara són les dels sistemes de numeració posicionals. També tenen representacions múltiples, i en un cert sentit les dificultats són més grans. Per exemple:

• En el sistema ternari equilibrat, ¹/₂ = 0,111… = 1,111…
• En el sistema de factoradic $1=1,000...=0,1234...$

Marko Petkovsek ha demostrat que aquestes ambigüitats són conseqüències necessàries de fet de fer servir un sistema posicional: per a qualsevol sistema d'aquest tipus que representa tots els nombres reals, el conjunt de reals amb representacions múltiples són sempre densos. Anomena la demostració «un exercici instructiu de topologia de conjunt de punts elemental». Això implica veure conjunts de valors posicionals com espais de Stone i observar que les seves representacions reals són expressades per funcions contínues.

Aplicacions

Una aplicació de 0,999… com a representació d'1 es dona en la teoria de nombres elemental. L'any 1802, H. Goodwin publicà una observació sobre l'aparició de xifres 9 en les representacions, en forma de decimals que es repeteixen, de les fraccions en les quals els denominadors són uns determinats nombres primers. Els exemples inclouen:

• ¹/₇ = 0,142857142857… i 142 + 857 = 999.
• ¹/₇₃ = 0,0136986301369863… i 0136 + 9863 = 9999.

El 1836, E. Midy demostrava un resultat general sobre tals fraccions, que s'ha anomenat teorema de Midy. La publicació era poc clara, i era confusa si la seva demostració implicava directament 0,999…, però com a mínim una demostració moderna de W. G. Leavitt sí que ho fa. Si es pot demostrar que un decimal de la forma 0,b₁b₂b₃… és un enter positiu, llavors ha de ser 0,999…, que és llavors la font de les xifres 9 en el teorema. Les investigacions en aquesta direcció poden motivar conceptes tals com el dels màxims comuns divisors, l'aritmètica modular, els nombres primers de Fermat, l'ordre d'elements d'un grup, i la reciprocitat quadràtica.

Posicions de ¹/₄, ²/₃ i 1 en el conjunt de Cantor.

Si es torna a l'anàlisi real, l'anàleg en base-3 $0,222...=1$ té un paper clau en una caracterització dels fractals més simples, en el conjunt de Cantor de terços mitjans: «Un punt en l'interval unitat és en el conjunt de Cantor si i només si es pot representar en base 3 fent servir només els dígits 0 i 2.»

L'n-èsim dígit de la representació reflecteix la posició del punt en l'n-èsima etapa de la construcció. Per exemple, al punt ²₃ se li dona la representació habitual de 0,2 o 0,2000…, ja que està situada a la dreta de la primera supressió i a l'esquerra de totes les supressions posteriors. El punt ¹/₃ es representa no com 0,1 sinó com 0,0222…, ja que és a l'esquerra de la primera supressió i a la dreta de totes les supressions posteriors.

Les xifres 9 repetides també apareixen en un altre dels treballs de Georg Cantor. Per construir una demostració vàlida s'han de tenir en compte: cal aplicar l'argument diagonal de 1891 a les expansions decimals la no numerabilitat de l'interval unitat. Aquesta demostració necessita ha de declarar que certs parells de nombres reals són diferents basant-se en les seves expansions decimals; d'aquesta manera cal evitar parells com 0,2 i 0,1999… Un mètode simple representa tots els nombres amb expansions que no s'acaben; el mètode oposat exclou repetir-ne de nous. Una variant que pot ser més propera a l'argument original de Cantor de fet fa servir la base 2; i transformant expansions en base-3 a expansions en base-2, també es pot demostrar la no numerabilitat del Conjunt de Cantor.

Escepticisme en l'ensenyament

Els estudiants de matemàtiques sovint rebutgen la igualtat de 0,999… i 1. Per raons motivades per qüestions que van des de la seva aparença dispar fins a malentesos profunds sobre el concepte de límit i desacords sobre la natura dels infinitesimals. Hi ha molts factors comuns que contribueixen a la confusió:

• Els estudiants, per un procés mental, sovint es queden amb la idea que un nombre es pot representar per decimals només d'una manera. Veure dos decimals evidentment diferents que representen el mateix nombre sembla una paradoxa, problema que s'amplifica per l'aparició d'un nombre aparentment senzill de comprendre com és 1.
• La intuïció i l'ensenyament ambigu porten els estudiants a pensar en el límit d'una successió com una mena de procés infinit més que com un valor fix, ja que una successió no necessita arribar al seu límit. On els estudiants accepten la diferència entre una successió de nombres i el seu límit, podrien llegir "0,999…" que significa la successió més que el seu límit.
• Alguns estudiants es refereixen a 0,999… com una expressió numèrica que té un valor fix menor d'1 en un valor infinitesimal però diferent de zero.
• Alguns estudiants creuen que el valor d'una sèrie convergent és, en el millor dels casos, una aproximació ($0,{\bar {9}}\approx 1$).

Aquestes idees són errònies en el context dels nombres reals estàndards, encara que algunes poden ser vàlides en uns altres sistemes de nombres, ja sia inventats per a la seva utilitat matemàtica general o com a contraexemples instructius per entendre millor el que envolta al 0,999… Moltes d'aquestes explicacions les va trobar el professor David O. Tall, que ha estudiat característiques d'ensenyament i cognició que condueixen a alguns dels malentesos que va observar en els seus estudiants universitaris. Entrevistant als seus estudiants per determinar perquè inicialment la vasta majoria rebutjaven la igualtat, trobà que «els estudiants continuaven concebent 0,999… com una successió de nombres més i més propers a 1 i no com un valor fix, perquè "no s'havia especificat quants llocs hi ha" o "és el decimal més a prop possible per sota d'1"».

De les proves elementals, multiplicant 0,333… = ¹/₃ per 3 és aparentment una estratègia d'èxit per a convèncer estudiants reticents que $0,999...=1$. Tanmateix, quan s'enfronten amb el conflicte entre la seva creença en la primera equació i la seva incredulitat en la segona, alguns estudiants comencen a dubtar de la primera equació o, simplement, se senten frustrats. No hi ha mètodes més sofisticats a prova de bomba: els estudiants que són plenament capaços d'aplicar definicions rigoroses encara poden recórrer a imatges intuïtives quan queden sorpresos amb un resultat de matemàtiques avançades, incloent-hi 0,999… Per exemple, un estudiant d'anàlisi real era capaç de demostrar que 0,333… = ¹/₃ fent servir la definició de suprem, però llavors insistia en el fet que 0,999… < 1 basant-se en la seva comprensió anterior de divisió llarga. Altres encara poden demostrar que ¹/₃ = 0,333… però, en enfrontar-se a la demostració basada en les fraccions, insisteixen en el fet que "la lògica" substitueix als càlculs matemàtics.

Joseph Mazur explica la història d'un estudiant de càlcul altrament brillant que «desafiava gairebé tot allò que jo deia a classe però mai no qüestionava la seva calculadora», i que havia arribat a creure que nou dígits són tots els que es necessita per fer matemàtiques, incloent-hi calcular l'arrel quadrada de 23. L'estudiant romania incòmode amb un argument restrictiu del tipus $9,99...=10$ anomenant-lo un «procés de creixement infinit salvatgement imaginat.»

Recentment, el 2005, com a part de la "teoria d'APOS" d'Ed Dubinsky sobre l'aprenentatge matemàtic, Dubinsky i els seus col·laboradors proposaren que els estudiants que conceben 0,999… com a cadena finita, indeterminada amb una distància infinitament petita des de l'1, no havien construït encara una concepció completa del decimal infinit". Altres estudiants que tenen una concepció completa de 0,999… encara poden no ser capaços d'"encapsular" aquest procés en una "concepció d'objecte", com la concepció d'objecte que tenen d'1, i així veuen el procés 0,999… i l'objecte 1 com a incompatibles. Aquests autors també connecten aquesta habilitat mental d'encapsulació amb veure ¹₃ com a nombre de ple dret i a tractar amb el conjunt de nombres naturals com una totalitat.

En la cultura popular

Amb l'expansió d'Internet, els debats sobre 0,999… han sortit de l'aula i ha estat el tema d'alguns grups de discussió i grups de notícies, incloent-n'hi molts que nominalment tenen poc a veure amb les matemàtiques. En el grup de discussió sci.math, discutir sobre 0,999… és un "esport popular", i és una de les preguntes que cal contestar en les seves PMF. Breument, el Faq cobreix ¹/₃, multiplicacions per 10, límits, i també al·ludeix a les successions de Cauchy.

Una edició de 2003 del diari d'interès general The Straight Dope discuteix sobre el 0,999… mitjançant ¹₃ i límits. Sobre les males interpretacions comenten:

El primat que hi ha en nosaltres encara resisteix, dient: 0,999~ no representa realment un "nombre", sinó un "procés". Per trobar un nombre hem d'aturar el procés, punt en el qual es desfà la qüestió de 0,999~ = 1. Bestieses.

The Straight Dope, en la seva pròpia pàgina de missatges, cita una discussió què havia succeït en una "altra pàgina de missatges" no identificada: «… principalment sobre videojocs». En la mateixa línia, la qüestió del 0,999… durant els primers set anys dels fòrums de Battle.net de Blizzard Entertainment, ha demostrat ser un tema tan popular que la companyia va arribar a emetre un "comunicat de premsa" el dia dels innocents (que als EUA és l'abril) de 2004, tot oferint dues demostracions, basades en límits i la multiplicació per 10. El comunicat deia:

Estem entusiasmats per poder passar pàgina sobre aquest tema d'una vegada per totes. Hem presenciat el maldecap i la preocupació sobre si 0,999~ és o no és igual a 1, i estem orgullosos que la següent demostració de manera terminal i decisiva resolgui la qüestió per als nostres clients.

0,999… apareix també en folklore matemàtic, específicament en el següent acudit:

P: Quants matemàtics calen per a caragolar una bombeta?

R: 0,999999…

0,999… en sistemes de nombres alternatius

Encara que els nombres reals formen un sistema de nombres extremadament útil, la decisió d'interpretar la notació "0,999…" tot anomenant-lo com un nombre real és en el fons una convenció, i Timothy Gowers sosté que la identitat 0,999… = 1 és també una convenció:

Tanmateix, no és una convenció arbitrària, perquè no obliga a adoptar-la a la força, o a inventar nous objectes estranys, o a abandonar algunes de les regles familiars de l'aritmètica.

Es poden definir altres sistemes de nombres que utilitzen regles diferents o nous objectes. En alguns d'aquests sistemes de nombres, les demostracions citades necessitarien ser reinterpretades i es podria trobar que en un sistema de nombres donat 0,999… i 1 podrien no ser idèntics. Tot i així, més que alternatives independents, molts sistemes de nombres són ampliacions del sistema de nombres reals. D'aquesta manera la igualtat $0,999...=1$ es pot continuar mantenint. Fins i tot en aquests sistemes de nombres, és interessant examinar sistemes de nombre alternatius, no només pel comportament de 0,999… —perquè, en efecte, un nombre expressat com "0,999…" és tant significatiu com inequívoc—, sinó també pel comportament de determinats fenòmens relacionats. Si aquests fenòmens difereixen d'aquells en el sistema de nombres reals, llavors com a mínim una de les suposicions construïdes en el sistema s'ha de desfer.

Infinitesimals

Article principal: Infinitesimal

Algunes demostracions de $0,999...=1$ es basen en la propietat arquimediana dels nombres reals estàndards que afirma que no hi ha cap infinitesimal diferent de zero. Hi ha estructures algebraiques ordenades matemàticament de manera coherent, incloent-hi diverses alternatives als nombres reals estàndards, que no són arquimedianes. El significat de 0,999… depèn de quina estructura es fa servir. Per exemple, els nombres duals inclouen un element infinitesimal nou (ε), anàleg a la unitat imaginària i en els nombres complexos excepte que ε²=0. L'estructura que resulta és útil en la diferenciació automàtica. Als nombres duals se'ls pot donar un ordre lexicogràfic; en aquest cas, els múltiples d'ε es converteixen en elements no arquimedians. Cal observar, tanmateix, que com a ampliació dels nombres reals els nombres duals encara mantenen que $0,999...=1$. Mentre que ε existeix en els nombres duals, una altra observació relacionada és que també ho compleix ε/2; de manera que ε no és "el nombre dual positiu més petit" i, en efecte, com en els reals, tal nombre no existeix.

L'anàlisi no estàndard subministra un sistema de nombres amb una plena varietat d'infinitesimals, i els seus inversos. A.H. Lightstone desenvolupà una expansió decimal per als nombres reals no estàndards dins de (0, 1)^∗. L'autor mostra com associar a cada nombre real no estàndard una seqüència de dígits

0.d₁d₂d₃…;…d_∞−1d_∞d_∞+1…

indexada pels nombres naturals estesos. Encara que no parla directament de 0,999…, mostra que el nombre real 1/3 queda representat per $0,333...,333...$ que és una conseqüència del principi de transferència. Multiplicant per 3, s'obtenen fets anàlegs per a expansions amb xifres 9 repetides.

El nombre hiperreal u_H = 0,999…;;…999000… amb H -una quantitat infinita de xifres 9, per a algun hiperenter infinit H, satisfà una desigualtat estricta u_H < 1. En efecte, la successió u₁ = 0,9, u₂ = 0,99, u₃ = 0,999, etc. satisfà u_n = 1 - 1/n. Per això, pel principi de transferència, u_H = 1 - 1/H < 1. Lightstone mostra que en aquest sistema $0,333...;...000...i0,999...;...000...$ no són nombres.

La teoria de jocs combinatòria també proporciona nombres reals alternatius, amb el joc infinit Hackenbush (blau-vermell) com un exemple especialment pertinent. El 1974, Elwyn Berlekamp descrivia una correspondència entre les cadenes del joc Hackenbush i les expansions binàries de nombres reals, motivada per la idea d'una compressió de dades. Per exemple, el valor de la cadena Hackenbush LRRLRLRL… és 0,010101₂… = ¹/₃. Tanmateix, el valor de LRLLL… (corresponent a 0,111…₂) és infinitessimalment menor que 1. La diferència entre el dos és el nombre subreal ¹/_ω, on ω és el primer ordinal infinit; el joc pertinent és LRRRR… o 0,000…₂.

Resta truncada

Una altra forma en la qual les proves podrien fallar és si l'operació "1 menys 0,999…" simplement no existeix, perquè la resta no és sempre possible. Les estructures matemàtiques amb una operació d'addició, però no amb una operació de sostracció (resta), inclouen semigrups commutatius, monoides commutatius i semianells. Richman considera aquests sistemes dissenyats de manera que 0,999… < 1.

Primer, Richman defineix un "nombre decimal" no-negatiu com una expansió decimal literal. Defineix l'ordre lexicogràfic i una operació d'addició, i es fixa en el fet que 0,999… < 1 simplement perquè 0 < 1 està en el lloc de les unitats, però per a qualsevol x infinit, es té $0,999...+''x''=1+''x''$. D'aquesta manera una peculiaritat dels nombres decimals és que l'addició no sempre pot ser cancel·lada. Una altra peculiaritat és que cap nombre decimal no correspon a ¹₃. Després de definir la multiplicació, els nombres decimals formen un semianell positiu, totalment ordenat, commutatiu.

En procés de definir la multiplicació, Richman també defineix un altre sistema que anomena "tall D", que és el conjunt de talls de Dedekind de fraccions decimals. Normalment, aquesta definició condueix als nombres reals, però per a una fracció decimal d permet ambdós talls: el tall (−∞, d) i el "tall principal" (−∞, d]. El resultat és que els nombres reals "estan vivint molestament junts" amb les fraccions decimals. Una altra vegada 0,999… < 1. No hi ha cap infinitesimal positiu en el tall D, però hi ha "una classe d'infinitesimals negatius", 0⁻, que no té cap expansió decimal. Conclou que 0,999… = 1 + 0⁻, mentre l'equació "0,999… + x = 1" no té cap solució.

Nombres p-àdics

Article principal: Nombre p-àdic

Quan es pregunta per 0,999…, els novells sovint creuen que hi hauria d'haver un "9 final", creient que 1 − 0,999… és un nombre positiu que escriuen com a "0,000…1". Tant si això té sentit com si no, l'objectiu intuïtiu és clar: afegint-ne un 1 a l'últim 9 de 0,999… portaria que les xifres 9 es transformessin en zeros, tot porta un 1 a la posició de les unitats. Entre altres raons, aquesta idea és errònia perquè no hi ha "finalment" un 9 a 0,999… Tanmateix, hi ha un sistema que conté una cadena infinita de xifres 9, incloent-hi un darrer 9.

Els enters 4-àdics (els punts negres), incloent-hi la seqüència (3, 33, 333, …) que convergeix a −1. L'anàleg 10-adic és …999 = −1.

Els nombres p-àdics són un sistema de nombres alternatiu d'interès en la teoria de nombres. Com els nombres reals, els nombres p-àdics es poden construir a partir dels nombres racionals via successions de Cauchy. La construcció fa servir una mètrica diferent en la qual 0 és més proper a p, i molt més proper a pⁿ, del que ho és a 1. Els nombres p-àdics formen un cos si p és un nombre primer i un anell per altres valors de p, incloent-hi 10. Per tant, l'aritmètica es pot desenvolupar en els nombres p -àdics, i no hi ha cap infinitesimal.

En els nombres 10-àdics, els anàlegs de les expansions decimals s'escriuen cap a l'esquerra. L'expansió 10-àdica …999 té un últim 9, i no té un primer 9. Es pot sumar 1 al lloc de les unitats, i tan sols queden zeros després de calcular $1+...999=...000=0$, i d'aquesta manera ...999 = −1. Una altra derivació fa servir una sèrie geomètrica. La sèrie infinita implicada per "…999" no convergeix en els nombres reals, però convergeix en els nombres 10-àdics, i així es pot reutilitzar la fórmula familiar:

$\ldots 999=9+9(10)+9(10)^{2}+9(10)^{3}+\cdots ={\frac {9}{1-10}}=-1.$

(compareu-ho amb la sèrie de més amunt)

Una tercera derivació la va inventar un estudiant de setè grau que dubtava de l'argument restrictiu del seu professor sobre 0,999… = 1 però es va inspirar en la prova de multiplicar per 10 de més amunt en la direcció oposada: si x = …999 llavors 10x = …990, així 10x = x − 9, per això x = −1 una altra vegada.

Com a ampliació final, de 0,999…; = 1 (en els reals) i …999 = −1 (en els 10-àdics), llavors per "fe cega i impertorbable en fer jocs malabars de símbols" es poden afegir les dues equacions i arribar a …999.999… = 0. Aquesta equació no té sentit ni com una expansió de nombres 10-àdics ni com una expansió decimal corrent, però resulta ser significativa i veritable si es desenvolupa una teoria de "dobles decimals" amb extrems esquerres eventualment repetitius. Representa un sistema familiar: els nombres reals.

Qüestions relacionades

• Les paradoxes de Zenó, especialment la paradoxa del corredor, són reminiscències de l'aparent paradoxa que afirma que 0,999… i 1 són iguals. La paradoxa del corredor es pot modelitzar matemàticament i llavors —com en el cas de 0,999…— es pot resoldre fent servir una sèrie geomètrica. Tanmateix, no queda clar si aquest tractament matemàtic encaixa amb els assumptes metafísics subjacents que Zenó estava explorant.
• La divisió entre zero ocorre en algunes discussions populars de 0,999… Mentre que la majoria dels autors decideixen definir 0,999… gairebé qualsevol tractament actual deixa sense definir la divisió entre zero, atès que no se li pot donar cap significat en els nombres reals estàndards. Tanmateix, la divisió entre zero es defineix en alguns altres sistemes, com a l'anàlisi complexa, on el pla complex estès, és a dir l'esfera de Riemann, té un "punt de l'infinit". Aquí, té sentit definir que ¹/₀ sigui infinit; i, de fet, els resultats són profunds i aplicables a molts problemes en enginyeria i física. Alguns prominents matemàtics advocaven a favor d'una definició com aquesta molt abans que es desenvolupés qualsevol sistema de nombres.
• El zero negatiu és un altre tret redundant de molts sistemes d'escriptura de nombres. En sistemes de nombres com per exemple, el dels nombres reals, on "0" denota la identitat additiva i no és ni positiu ni negatiu, la interpretació habitual de "−0" és que hauria de denotar la inversa de l'addició de 0, que força la igualtat −0 = 0. No obstant això, algunes aplicacions científiques utilitzen per separat el zero positiu i el zero negatiu, com ho fan alguns sistemes de nombres més habituals en ordinadors —per exemple enters emmagatzemats amb signe i magnitud— els formats de complement a u, o nombres de coma flotant com s'especifiquen al IEEE floating-point).

Vegeu també

• Infinit
• límit (matemàtiques)
• Anàlisi real
• Sèrie matemàtica

Bibliografia

• Alligood, Sauer, and Yorke. «4.1 Cantor Sets». A: Chaos: An introduction to dynamical systems. Springer, 1996. ISBN 0-387-94677-2. 
• Apostol, Tom M. Mathematical analysis. 2a ed.. Addison-Wesley, 1974. ISBN 0-201-00288-4. 
• Bartle, R.G. and D.R. Sherbert. Introduction to real analysis. Wiley, 1982. ISBN 0-471-05944-7. 
• Beals, Richard. Analysis. Cambridge UP, 2004. ISBN 0-521-60047-2. 
• Berlekamp, E.R.; Conway, J.H.; Guy, R.K.. Winning Ways for your Mathematical Plays. Academic Press, 1982. ISBN 0-12-091101-9. 
• Berz, Martin (1992). "Automatic differentiation as nonarchimedean analysis". Computer Arithmetic and Enclosure Methods: 439–450, Elsevier 
• Bunch, Bryan H. Mathematical fallacies and paradoxes. Van Nostrand Reinhold, 1982. ISBN 0-442-24905-5. 
• Burrell, Brian. Merriam-Webster's Guide to Everyday Math: A Home and Business Reference. Merriam-Webster, 1998. ISBN 0-87779-621-1. 
• Conway, John B. [1973]. Functions of one complex variable I. 2a ed.. Springer-Verlag, 1978. ISBN 0-387-90328-3. 
• Davies, Charles. The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications. A.S. Barnes, 1846. 
• DeSua, Frank C. «A system isomorphic to the reals». The American Mathematical Monthly, 67, 9, novembre 1960, pàg. 900–903. DOI: 10.2307/2309468.
• Dubinsky, Ed, Kirk Weller, Michael McDonald, and Anne Brown «Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2». Educational Studies in Mathematics, 60, 2005, pàg. 253–266. DOI: 10.1007/s10649-005-0473-0.
• Edwards, Barbara and Michael Ward «Surprises from mathematics education research: Student (mis)use of mathematical definitions» (PDF). The American Mathematical Monthly, 111, 5, maig 2004, pàg. 411–425. DOI: 10.2307/4145268.
• Enderton, Herbert B. Elements of set theory. Elsevier, 1977. ISBN 0-12-238440-7. 
• Euler, Leonhard [1770]. John Hewlett and Francis Horner, English translators.. Elements of Algebra. 3a ed.. Orme Longman, 1822. 
• Fjelstad, Paul «The repeating integer paradox». The College Mathematics Journal, 26, 1, gener 1995, pàg. 11–15. DOI: 10.2307/2687285.
• Gardiner, Anthony [1982]. Understanding Infinity: The Mathematics of Infinite Processes. Dover, 2003. ISBN 0-486-42538-X. 
• Gowers, Timothy. Mathematics: A Very Short Introduction. Oxford UP, 2002. ISBN 0-19-285361-9. 
• Grattan-Guinness, Ivor. The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press, 1970. ISBN 0-262-07034-0. 
• Griffiths, H.B.; P.J. Hilton. A Comprehensive Textbook of Classical Mathematics: A Contemporary Interpretation. Londres: Van Nostrand Reinhold, 1970. ISBN 0-442-02863-6. 
• Kempner, A.J. «Anormal Systems of Numeration». The American Mathematical Monthly, 43, 10, desembre 1936, pàg. 610–617. DOI: 10.2307/2300532.
• Komornik, Vilmos; and Paola Loreti «Unique Developments in Non-Integer Bases». The American Mathematical Monthly, 105, 7, 1998, pàg. 636–639. DOI: 10.2307/2589246.
• Leavitt, W.G. «A Theorem on Repeating Decimals». The American Mathematical Monthly, 74, 6, 1967, pàg. 669–673. DOI: 10.2307/2314251.
• Leavitt, W.G. «Repeating Decimals». The College Mathematics Journal, 15, 4, setembre 1984, pàg. 299–308. DOI: 10.2307/2686394.
• Lewittes, Joseph. «Midy's Theorem for Periodic Decimals». New York Number Theory Workshop on Combinatorial and Additive Number Theory. arXiv, 2006.
• Lightstone, A.H. «Infinitesimals». The American Mathematical Monthly, 79, 3, març 1972, pàg. 242–251. DOI: 10.2307/2316619.
• Mankiewicz, Richard. The story of mathematics. Cassell, 2000. ISBN 0-304-35473-2. 
• Maor, Eli. To infinity and beyond: a cultural history of the infinite. Birkhäuser, 1987. ISBN 3-7643-3325-1. 
• Mazur, Joseph. Euclid in the Rainforest: Discovering Universal Truths in Logic and Math. Pearson: Pi Press, 2005. ISBN 0-13-147994-6. 
• Munkres, James R. [1975]. Topology. 2a ed.. Prentice-Hall, 2000. ISBN 0-13-181629-2. 
• Núñez, Rafael. «Do Real Numbers Really Move? Language, Thought, and Gesture: The Embodied Cognitive Foundations of Mathematics». A: 18 Unconventional Essays on the Nature of Mathematics. Springer, 2006, p. 160–181. ISBN 978-0-387-25717-4. 
• Pedrick, George. A First Course in Analysis. Springer, 1994. ISBN 0-387-94108-8. 
• Petkovšek, Marko «Ambiguous Numbers are Dense». American Mathematical Monthly, 97, 5, maig 1990, pàg. 408–411. DOI: 10.2307/2324393.
• Pinto, Márcia; Tall, David. «Following students' development in a traditional university analysis course» (PDF). PME25 p. v4: 57–64, 2001. [Consulta: 3 maig 2009].
• Protter, M.H. i Morrey, C.B.. A first course in real analysis. 2a ed.. Springer, 1991. ISBN 0-387-97437-7. 
• Pugh, Charles Chapman. Real mathematical analysis. Springer-Verlag, 2001. ISBN 0-387-95297-7. 
• Renteln, Paul and Allan Dundes «Foolproof: A Sampling of Mathematical Folk Humor» (PDF). Notices of the AMS, 52, gener 2005, pàg. 24–34 [Consulta: 3 maig 2009].
• Richman, Fred «Is 0.999… = 1?». Mathematics Magazine, 72, 5, desembre 1999, pàg. 396–400. Free HTML preprint: Richman, Fred. «Is 0.999… = 1?», 08-06-1999. Arxivat de l'original el 2006-02-03. [Consulta: 23 agost 2006]. Note: the journal article contains material and wording not found in the preprint.
• Robinson, Abraham. Non-standard analysis. Revised. Princeton University Press, 1996. ISBN 0-691-04490-2. 
• Rosenlicht, Maxwell. Introduction to Analysis. Dover, 1985. ISBN 0-486-65038-3. 
• Rudin, Walter [1953]. Principles of mathematical analysis. 3a ed.. McGraw-Hill, 1976. ISBN 0-07-054235-X. 
• Shrader-Frechette, Maurice «Complementary Rational Numbers». Mathematics Magazine, 51, març 1978, pàg. 90–98.
• Smith, Charles and Charles Harrington. Arithmetic for Schools. Macmillan, 1895. 
• Sohrab, Houshang. Basic Real Analysis. Birkhäuser, 2003. ISBN 0-8176-4211-0. 
• Stewart, Ian. The Foundations of Mathematics. Oxford UP, 1977. ISBN 0-19-853165-6. 
• Stewart, James. Calculus: Early transcendentals. 4a ed.. Brooks/Cole, 1999. ISBN 0-534-36298-2. 
• D.O. Tall and R.L.E. Schwarzenberger «Conflicts in the Learning of Real Numbers and Limits» (PDF). Mathematics Teaching, 82, 1978, pàg. 44–49 [Consulta: 3 maig 2009].
• Tall, David «Conflicts and Catastrophes in the Learning of Mathematics» (PDF). Mathematical Education for Teaching, 2, 1976/7, pàg. 2–18 [Consulta: 3 maig 2009].
• Tall, David «Cognitive Development In Advanced Mathematics Using Technology» (PDF). Mathematics Education Research Journal, 12, 2000, pàg. 210–230 [Consulta: 3 maig 2009].
• Thompson, Silvanus P. Calculus Made Easy. Nova York: St. Martin's Press, 1998. ISBN 0-312-18548-0.  (primera edició el 1910).
• von Mangoldt, Dr. Hans. «Reihenzahlen». A: Einführung in die höhere Mathematik (en alemany). 1a edició. Leipzig: Verlag von S. Hirzel, 1911. 
• Wallace, David Foster. Everything and more: a compact history of infinity. Norton, 2003. ISBN 0-393-00338-8. 

Enllaços externs

• .999999… = 1? a Cut-the-knot.. (anglès)
• Ask A Scientist: Repeating Decimals Arxivat 2015-02-26 a Wayback Machine.. (anglès)
• Proof of the equality based on arithmetic. (anglès)
• Point nine recurring equals one. (anglès)
• Theorem 0.999... a Metamath. (anglès)
• "A Friendly Chat About Whether 0.999… = 1". (anglès)