Cinètica química

Exemple d'una gràfica de concentració respecte del temps qualsevol, on es parteix d'un reactiu inicial que disminueix la seva concentració mentre el producte l'augmenta.

La cinètica química, també coneguda com a velocitat de reacció, és l'estudi de la velocitat de les reaccions químiques i dels factors dels quals depèn. La cinètica química inclou investigacions de com els diferents factors experimentals poden influir en la velocitat d'una reacció química, sobre el mecanisme de reacció i els estats de transició; així com la construcció de models matemàtics que poden descriure les característiques d'una reacció química a priori de l'experiència.

La cinètica química és un estudi empíric i experimental, però la química quàntica ha permès indagar en les mecàniques de la reacció, que origina la dinàmica química. I el 1864, Peter Waage i Guldberg Cato van formular la llei d'acció de masses i van ser pioners en el desenvolupament de la cinètica química, que estableix que la velocitat d'una reacció química és proporcional a la quantitat de les substàncies que reaccionen.

Al principi de la reacció, quan la concentració de reactius és alta, la probabilitat que les molècules dels reactius xoquin és més alta i per tant la velocitat també ho és; a mesura que la reacció progressa, la concentració de reactius disminueix gradualment i arriba a zero quan tota la substància ha reaccionat.

Hi ha un gran interès per controlar la velocitat de les reaccions químiques, ja que, per exemple, les reaccions responsables de la putrefacció dels aliments interessa que siguin el més lentes possible. En canvi, les reaccions implicades en processos productius han de ser ràpides per tal d'aconseguir millor rendiment.

Factors que afecten a la velocitat d'una reacció química

Dibuix il·lustratiu de l'efecte de l'augment de la concentració en una reacció química, augmenten les col·lisions.

Aquests factors són:

• la concentració dels reactius
• la temperatura
• influència d'un catalitzador o inhibidor
• la naturalesa dels reactius
• el grau de divisió dels reactius i la seva disposició
• la pressió

Velocitat de la reacció

Sempre s'ha de tenir en compte que la velocitat d'aparició d'un producte és proporcional a la velocitat de desaparició d'un reactiu. Experimentalment, es pot determinar la velocitat mitjana d'una reacció mitjançant l'expressió següent:

$v_{\rm {m}}={\frac {\Delta c}{\Delta t}}={\frac {c_{\rm {f}}-c_{0}}{t_{\rm {f}}-t_{0}}}$

On $c$ és la concentració i $t$ és el temps.

Matemàticament, la velocitat a la qual es produeix una reacció química (velocitat de reacció) relaciona el canvi en la concentració (normalment en molaritat: mols solut / litre dissolució) dels reactius o els productes amb el temps. I en les unitats del Sistema Internacional d'Unitats s'expressa com a ${\rm {\textstyle (mol/L\cdot s)}}$. Per exemple:

${\rm {N_{2}+3\,H_{2}\longrightarrow 2\,NH_{3}}}$

I així, la variació de la concentració, matemàticament, queda determinada segons les expressions següents:

$v_{\rm {N_{2}}}=-{\frac {\mathrm {d[N_{2}]} }{\mathrm {d} t}}$

$v_{\rm {H_{2}}}=-{\frac {\mathrm {d[H_{2}]} }{\mathrm {d} t}}$

$v_{\rm {NH_{3}}}={\frac {\mathrm {d[NH_{3}]} }{\mathrm {d} t}}$

On $v_{\rm {N_{2}}}$ és la velocitat de reacció del nitrogen, on $v_{\rm {H_{2}}}$ és la velocitat de l'hidrogen i on $v_{\rm {NH_{3}}}$ és la velocitat de l'amoníac. Òbviament, la concentració dels reactius és negativa, ja que disminueix, mentre que la dels productes (l'amoníac) és positiva, ja que augmenta. I llavors, en igualar les tres fórmules de velocitat ens resulta la següent igualació:

$v=-{\frac {\mathrm {d[N_{2}]} }{\mathrm {d} t}}={\frac {1}{3}}\cdot {\frac {-\mathrm {d[H_{2}} ]}{\mathrm {d} t}}={\frac {1}{2}}\cdot {\frac {\mathrm {d[NH_{3}]} }{\mathrm {d} t}}$

Això significa que en el temps que reacciona una unitat de nitrogen, reacciona un terç d'hidrogen i una meitat d'amoníac. Com es pot comprovar, la velocitat, en part, ve determinada pels coeficients estequiomètrics de la mostra que reacciona.

Equació de velocitat

L'equació de velocitat és una fórmula que expressa la relació d'una reacció i les concentracions de reactius a una temperatura determinada. Es parteix d'una reacció qualsevol:

$a\mathrm {A} +b\mathrm {B} \longrightarrow \mathrm {productes}$

I d'aquesta reacció, tenim que l'equació és igual a:

$v=k\cdot \mathrm {[A]} ^{\alpha }\cdot \mathrm {[B]} ^{\beta }$

On $\alpha$ i $\beta$ són l'ordre parcial de la reacció. I on $\alpha +\beta$ són l'ordre total de la reacció i $k$ la constant de velocitat, que té unitats variables depenent de l'ordre total de la reacció i depèn de la temperatura i la presència de catalitzadors o inhibidors. L'equació de velocitat d'una reacció només es pot determinar empíricament i només és aplicable als reactius de la reacció.

Ordre de reacció

La fórmula de la reacció, i les unitats de la $k$, depenen de l'ordre total de la reacció. I per exemple, fins a l'ordre 3:

Ordre total	Reacció d'ordre	Velocitat	Unitats de la $k$
$\alpha +\beta =0$	0	$v=k$	$k=\left[{\rm {\frac {mol}{L\cdot s}}}\right]$
$\alpha +\beta =1$	1	$v=k\cdot {\rm {[A]}}$	$k=\left[{\rm {\frac {1}{s}}}\right]$
$\alpha +\beta =2$	2	$v=k\cdot {\rm {[A]^{2}}}$ o bé $v=k{\rm {\cdot [A]\cdot [B]}}$	$k=\left[{\rm {\frac {L}{mol\cdot s}}}\right]$
$\alpha +\beta =3$	3	$v=k{\rm {\cdot [A]^{2}\cdot [B]}}$ o bé $v=k{\rm {\cdot [A]\cdot [B]^{2}}}$	$k=\left[{\rm {\frac {L^{2}}{mol^{2}\cdot s}}}\right]$

Determinació dels ordres de reacció no donats

Segons unitats

Una manera d'esbrinar l'ordre d'una reacció que no ens han donat és mitjançant la k. Si sabem les seves unitats podem deduir-ne l'ordre de reacció.

Ordre de reacció 0

Si $k=\mathrm {\left[{\frac {mol}{L\cdot s}}\right]} \longrightarrow v=k{\rm {\cdot [A]^{\alpha }\cdot [B]^{\beta }}}$

${\rm {\left[{\frac {mol}{L\cdot s}}\right]=\left[{\frac {mol}{L\cdot s}}\right]\cdot \left[{\frac {mol}{L}}\right]^{0}}}$

Com es pot comprovar, com que el resultat final de la velocitat ha de ser en unitats del SI, i la k ja ens dona aquestes unitats, forçosament la concentració de A ha d'estar elevada a 0 perquè així s'iguala l'equació. Llavors si alfa més beta és igual a zero, l'ordre total de la reacció és zero.

Ordre de reacció 1

Si $k=\mathrm {\left[{\frac {1}{s}}\right]} \longrightarrow v=k{\rm {\cdot [A]^{\alpha }\cdot [B]^{\beta }}}$

${\rm {\left[{\frac {mol}{L\cdot s}}\right]=\left[{\frac {1}{s}}\right]\cdot \left[{\frac {mol}{L}}\right]^{1}}}$

Ja es pot veure que el si multipliquem k, per a [A] elevat a 1 s'iguala l'equació i s'aconsegueixen les unitats del SI. Llavors es dedueix que l'ordre de reacció és 1.

Ordre de reacció 2

Si $k=\mathrm {\left[{\frac {L}{mol\cdot s}}\right]} \longrightarrow v=k{\rm {\cdot [A]^{\alpha }\cdot [B]^{\beta }}}$

${\rm {\left[{\frac {mol}{L\cdot s}}\right]=\left[{\frac {L}{mol\cdot s}}\right]\cdot \left[{\frac {mol}{L}}\right]^{2}\longrightarrow {\frac {L\cdot mol^{2}}{mol\cdot s\cdot L^{2}}}=\left[{\frac {mol}{L\cdot s}}\right]}}$

Com es pot veure, si elevem al quadrat [A] la igualació es compleix (que seria el mateix que multiplicar [A] per [B], en unitats). Al simplificar-se les unitats com es pot comprovar dona les unitats del SI com a resultat, demostrant que la igualació és correcte.

Donada una taula de dades

Si ens donen una taula de dades es pot esbrinar cadascun dels ordres de reacció mitjançant l'equació integrada de velocitat, on [A] varia en funció del temps. En el cas que la temperatura sigui constant, com que la k també serà constant, el pendent serà constant i en resultarà una recta gràficament. Per això trobem dos punts de l'equació, i al calcular el pendent ens donarà de resultat el valor de k.

A partir dels mecanismes de reacció

Un reacció química, de vegades, no es produeix tal com està escrita sinó que segueix una sèrie de reaccions elementals que globalment conformen la reacció escrita. El mecanisme de reacció són el són les diferents etapes que segueixen els reactius fins a transformar-se en els productes finals. Per tant, una reacció és elemental si només té una etapa, i és no elemental si en té més d'una.

Elementals

En l'equació de velocitat, els processos elementals compleixen que els ordres parcials ($\alpha$ i $\beta$) coincideixen amb els coeficients estequiomètrics de la concentració del seu reactiu, per exemple:

${\rm {A+2\,B\longrightarrow C}}$

Llavors com que A té coeficient estequiomètric 1 i B té coeficient estequiomètric 2 l'ordre de reacció és igual a 3:

$\alpha +\beta =3$

No elementals

En les no elementals els ordres de reacció parcials no coincideixen amb els coeficients estequiomètrics i llavors s'ha de determinar quina és la reacció parcial lenta, i relacionant els elements de la reacció ràpida, substituir-ho a l'etapa lenta i llavors trobar alfa i beta. Per explicar-ho millor es farà ús d'un exemple:

Gràfic de l'energia en funció de les coordenades de reacció, en una reacció química no elemental que realitza dues etapes abans de donar els productes finals. En la primera etapa dona uns productes mitjans endotèrmics, tot i que la reacció global és exotèrmica.

En el boirum fotoquímic, produït per les emissions de derivats del petroli, s'esdevé la reacció global:

$2{\rm {NO_{(g)}+O_{2(g)}\longrightarrow 2\,NO_{2(g)}}}$

Però en ser una reacció general, realment aquesta reacció no s'esdevé així sinó que té alguns passos enmig, té un mecanisme de reacció, que fa que no puguem aplicar l'equació de velocitats directament. Concretament és una reacció formada per dues etapes:

Reaccions parcials: ${\begin{cases}{\rm {NO_{(g)}+O_{2(g)}\leftrightarrow NO_{3(g)}}}\\NO_{3(g)}+NO_{g}\longrightarrow 2\,NO_{2(g)}\end{cases}}$

I llavors, com s'ha dit anteriorment, com que en l'equació de la llei de velocitats d'un procés elemental els ordres parcials coincideixen amb els coeficients estequiomètrics dels reactius es pot deduir que la reacció ràpida serà la primera i la lenta la segona. També a destacar, que els processos elementals ràpids són reversibles i poden arribar a l'equilibri. Un cop se sap quina és la reacció parcial lenta, que és la determinant de la reacció global, es fan els següents passos:

• Es parteix de la reacció lenta, suposant que és elemental:

$v=k{\rm {\cdot [NO_{3}]^{1}\cdot [NO]^{1}}}$

• Es relacionen els elements que hi ha en l'equació de velocitat global i no en la reacció parcial ràpida:

$K_{\rm {eq}}={\rm {\frac {[NO_{3}]}{[NO]\cdot [O_{2}]}}}$

• Finalment, se substitueixen els elements de l'equació de velocitat a l'etapa lenta i s'obtenen els ordres parcials de la reacció:

${\begin{cases}\mathrm {[NO_{3}]} =K_{\rm {eq}}\cdot \mathrm {[NO]} \cdot \mathrm {[O_{2}]} \\v=k\cdot \mathrm {[NO_{3}]^{1}\cdot [NO]^{1}} \end{cases}}$

$v=k\cdot [K_{\rm {eq}}{\rm {\cdot [NO]\cdot [O_{2}]]\cdot [NO]}}$

$v=k{\rm {\cdot [NO]^{2}\cdot [O_{2}]}}$

Aleshores, es comprova que $\alpha =2$ i $\beta =1$.

Anàlisi de dades i resultats cinètics

Les lleis i fórmules que s'usen a cinètica sempre són referides als reactius, per això mai no es pot aplicar l'equació de velocitats als productes. I a partir de les velocitats, es vol aconseguir arribar a l'expressió que ens diu la concentració d'un element al llarg del temps.

Fórmules

Depenent de l'ordre total de la reacció, s'usen unes fórmules o altres per a determinar la concentració, el temps de vida mitjana o la velocitat. La taula per les fórmules fins a l'ordre de reacció 2 és:

Ordre de la reacció	Equació de velocitat	Equació integrada	Temps de vida mitjana
0	$k\cdot \mathrm {[A]^{0}} ={\frac {-\mathrm {d[A]} }{\mathrm {d} t}}$ per tant, $v=k$	$\mathrm {[A]} =\mathrm {[A]_{0}} -k\cdot t$	$t_{1/2}={\frac {\mathrm {[A]_{0}} }{2\cdot k}}$
1	$k\cdot \mathrm {[A]^{1}} ={\frac {-\mathrm {d[A]} }{\mathrm {d} t}}$ per tant, $v=k\cdot [A]$	$\ln \left({\frac {\mathrm {[A]} }{\mathrm {[A]_{0}} }}\right)=-k\cdot t$	$t_{1/2}={\frac {\ln(2)}{k}}$
2	$k\cdot \mathrm {[A]^{2}} ={\frac {-\mathrm {d[A]} }{\mathrm {d} t}}$ per tant, $v=k\cdot {\rm {[A]^{2}}}$	${\frac {1}{\mathrm {[A]} }}={\frac {1}{\mathrm {[A_{0}]} }}+k\cdot t$	$t_{1/2}={\frac {1}{k\cdot {\rm {[A]_{0}}}}}$

L'equació d'Arrhenius i l'energia d'activació

Al 1889, Svante Arrhenius pensà que les reaccions devien necessitar algun tipus d'energia per començar a reaccionar, la que denominà l'energia d'activació d'una reacció. Aquesta energia, energia que prové de l'energia cinètica de les molècules que col·lideixen, és l'energia necessària perquè comenci la reacció, sempre és positiva. L'energia cinètica serveix per originar les reaccions, però si les molècules es mouen molt a poc a poc, les molècules només rebotaran en xocar amb altres molècules i la reacció no s'esdevindrà. I així Arrhenius formulà l'expressió:

$k=A\cdot {\mathrm {e} }^{-{\frac {E_{\rm {a}}}{RT}}}$

on:

$k(T)$: constant cinètica (depenent de la temperatura).

$A$: factor preexponencial d'Arrhenius i té les mateixes unitats que la constant cinètica.

$E_{\rm {a}}$: energia d'activació.

$R$: Constant universal dels gasos.

$T$: temperatura absoluta (K).

Que, tenint en compte que $A$ i $E_{\rm {a}}$ es poden considerar constants en un rang determinat de temperatures i es poden relacionar les constants de velocitat a dues temperatures, també es pot expressar com a:

$\ln \left({\frac {k_{2}}{k_{1}}}\right)=-{\frac {E_{\rm {a}}}{R}}\cdot \left({\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}\right)$

on:

$k_{1}$: constant cinètica (a temperatura inicial).

$k_{2}$: constant cinètica (a temperatura final).

$E_{\rm {a}}$: energia d'activació.

$R$: Constant universal dels gasos.

$T_{1}$: temperatura absoluta (K), inicial.

$T_{2}$: temperatura absoluta (K), final.

Models teòrics de la cinètica química

Hi ha dos grans models teòrics sobre la cinètica química, el primer és l'anomenada teoria de les col·lisions i la segona és la teoria de l'estat de transició.

Teoria de les col·lisions

Si per exemple es té una reacció de tipus ${\rm {A_{2(g)}+B_{2(g)}\longrightarrow C}}$, si la reacció és elemental (és a dir, s'esdevé tal com està escrita sense etapes), els valors d'alfa i beta han de ser els coeficients estequiomètrics i la seva llei de velocitat forçosament ha de ser:

$v=k\cdot {\rm {[A_{2}]\cdot [B_{2}]}}$

Aquesta teoria es basa en el concepte que les molècules dels reactius han de col·lidir per poder reaccionar, i postula els factors als quals està subjecta la velocitat de la reacció. La velocitat és proporcional a:

1) La freqüència de les col·lisions ($Z_{0}$).

2) Les concentracions dels reactius.

3) La part de les col·lisions en les quals les molècules estan correctament orientades (p).

4) La fracció de molècules que tenen l'energia suficient perquè la col·lisió entre ambdós molècules de reactiu sigui efectiva i permeti la reacció (${\mathrm {e} }^{-{\frac {E_{\rm {a}}}{RT}}}$).

Gràfic de l'energia en funció de les coordenades de reacció, en una reacció química endotèrmica...

... i d'una exotèrmica. Segons la teoria de l'estat de transició.

Per tant,

$v=Z_{0}\cdot p\cdot {\mathrm {e} }^{-{\frac {E_{\rm {a}}}{R\cdot T}}}\cdot {\rm {[A_{2}]\cdot [B_{2}]}}$

I llavors, de les anteriors equacions es dedueix que:

$k=Z_{0}\cdot p\cdot {\mathrm {e} }^{-{\frac {E_{\rm {a}}}{R\cdot T}}}$

I segons aquesta equació, la constant de velocitat depèn de forma exponencial de l'invers de la temperatura. I llavors, comparant les equacions s'extreu que A, el factor preexponencial d'Arrhenius, és:

$A=Z_{0}\cdot p$

Teoria de l'estat de transició

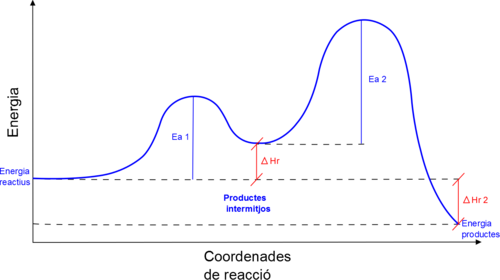
Aquest model explica la cinètica química mitjançant un estat entre els reactius i els productes. Aquest estat s'anomena estat de transició o complex activat. L'energia potencial de l'estat de transició és sempre superior a l'energia de reactius i productes, representada en les gràfiques com un petit turó, i representa la barrera energètica que han de superar els reactius perquè es produeixi la reacció i en resultin uns productes que poden tenir més o menys energia que els reactius però sempre amb menys energia que el complex activat. Aquesta energia necessària perquè es produeixi la reacció, el turó que ha de sobrepassar la reacció per donar-se, s'anomena energia d'activació de la reacció, i com més petita és l'energia d'activació, més ràpida és la reacció.

A més a més, aquest model, ens permet determinar si una reacció serà exotèrmica o endotèrmica en funció de la posició energètica dels reactius i productes. Si els productes estan per sobre dels reactius energèticament, serà un reacció endotèrmica, i si els productes són menys energètics, vol dir que han alliberat energia en forma de calor, i per tant serà una reacció exotèrmica.

Bibliografia

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Cinètica química

• Química per a l'enginyeria. Publicacions acadèmiques UPC, 2011, p. 338 (305-338). ISBN 978-84-7653-599-8. 
• Fogler, H Scott. Elements of Chemical Reaction Engineering. Prentice Hall, 2005. ISBN 978-0130473943. 
• José Ángel Hernández Santadaría, "Cinètica Química" a slideshare Arxivat 2013-05-05 a Wayback Machine.

Vegeu també

• Reactivitat química