Circuit en paral·lel
Circuit en paral·lel és un terme que s'utilitza en electricitat per referir-se a un circuit elèctric on els components (resistències, condensadors, fonts, ...) són en diferents branques, posats de manera que els respectius extrems són connectats entre si.
Característiques[modifica]
Els diferents receptors d'un circuit estan acoblats en paral·lel quan cadascun d'ells està connectat al pol positiu i al pol negatiu de la pila, de manera que estan alimentats per la mateixa tensió.
Les característiques de funcionament dels receptors en paral·lel són les següents:
- Cada receptor rep la mateixa tensió.
- Si s'espatlla o desconnectem un receptor, els altres continuen funcionant.
- El corrent elèctric total del circuit és la suma dels corrents de cada receptor.
Els receptors, en la majoria d'instal·lacions elèctriques, es connecten en paral·lel, perquè d'aquesta manera funcionen a la mateixa tensió i si falla algun d'ells, la resta continua funcionant.
Anàlisi[modifica]
En un circuit en paral·lel les branques són sotmeses a la mateixa tensió, al mateix voltatge, i tenen una polaritat idèntica. En canvi, el corrent no és el mateix atès que es divideix entre les diferents branques. El corrent total I és igual a la suma del corrent de cada branca, seguint la Llei d'Ohm tenim que:
- .
Notació[modifica]
Per simplificar les equacions, s'acostuma a representar la característica de ser en paral·lel com dues línies verticals . Així, per indicar que dues resistències són en paral·lel tindrien:
- .
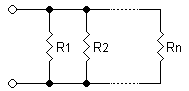
Resistències[modifica]
Per un circuit amb resistències en paral·lel, la resistència total seria:
Per trobar el corrent que hi haurà a un component amb resistència , utilitzarem la Llei d'Ohm:
- .
El corrent es divideix entre els components d'acord amb les respectives resistències, així, en el cas de dues resistències tenim:
- .
Inductors[modifica]
Per a un circuit amb inductors connectats en paral·lel tenim:
Si els inductors són situats dintre del camp magnètic dels altres, el valor anterior resultarà alterat. Si la inductància mútua entre dos inductors en paral·lel és M, la inductància equivalent serà:
o
i per tant
o
- .
El signe de dependrà de com els camps magnètics s'afecten els uns amb els altres. El principi és idèntic per més de dos inductors, però la inductància mútua entre ells ha de ser tinguda en consideració. Per tres inductors, hi haurà tres inductàncies mútues , and i vuit possibles equacions.
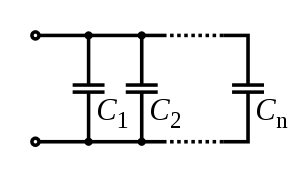
Condensadors[modifica]
Per a un circuit amb condensadors connectats en paral·lel:
La capacitat total serà igual a:
- .
Vegeu també[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Circuit en paral·lel |