Fórmula de Brahmagupta
En geometria, la fórmula Brahmagupta troba l'àrea de qualsevol quadrilàter donades les longituds dels costats i alguns dels angles. En la seva forma més comuna, s'obté l'àrea dels quadrilàters que es puguin inscriure en un cercle.
Forma Bàsica[modifica]
En la seva forma més bàsica i més fàcil de recordar, la fórmula Brahmagupta dona l'àrea d'un quadrilàter amb costats de longituds a , b , c , d , sempre que el quadrilàter sigui cíclic (els seus quatre vèrtexs estiguin sobre una mateixa circumferència):
on s , és el semiperímetre, així:
Aquesta fórmula generalitza la fórmula d'Heró per a l'àrea d'un triangle. De fet, la fórmula d'Heró poden derivar de la fórmula de Brahmagupta al permetre acostar-se a un valor de zero. Un triangle pot ser considerat com un quadrilàter amb un costat de longitud zero. Des d'aquesta perspectiva, com d tendeix a zero, un quadrilàter cíclic convergeix en un triangle cíclic (tots els triangles són cíclics), i la fórmula de Brahmagupta convergeix en la fórmula d'Heró.
L'afirmació que l'àrea del quadrilàter és donada per la fórmula de Brahmagupta és equivalent a l'afirmació que és igual a
fórmula de Brahmagupta pot ser vista com una fórmula de mediació longitud dels costats, sinó que també dona a la zona com una fórmula en l'altura des del centre cap als costats, encara que si el quadrilàter no conté el centre, l'altitud al costat més llarg ha de ser presa com a negativa.
La prova de la fórmula de Brahmagupta[modifica]
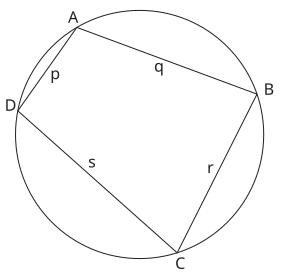
Àrea de la Zona quadrilàter cíclic = Àrea de Àrea de
Però des és un quadrilàter cíclic, Per tant, Per Tant
Aplicant el teorema del cosinus per i i igualant les expressions per al costat , tenim
Substituint (ja que els angles són complementaris) i reordenant, hem de
Substituint aquesta expressió en l'equació per a l'àrea,
que és de la forma i per tant es pot escriure en la forma com,
Introduint
Prenent l'arrel quadrada, obtenim
Extensió als Quadrilàters no cíclics[modifica]
En el cas dels quadrilàters cíclics no, la fórmula de Brahmagupta pot estendre's en considerar les mesures de dos angles oposats del quadrilàter
on θ és la meitat de la suma de dos angles oposats. (La parella és irrellevant: si es donen els altres dos angles, la meitat de la seva suma és el suplement de θ. Com que cos (180 ° - θ) =-cosq, tenim cos 2 (180 ° - θ) = cos 2 θ.) Es desprèn d'això que l'àrea d'un quadrilàter cíclic és l'àrea màxima possible per a qualsevol quadrilàter per unes longituds de costats donades.
Aquesta fórmula general es coneix de vegades com la fórmula de Bretschneider, però d'acord amb MathWorld aquesta forma es deu, sembla, a Coolidge, l'expressió de Bretschneider va ser
on p i q són les longituds de les diagonals del quadrilàter. Aquesta fórmula també demostra el teorema de Ptolemeu generalitzat.
És una característica dels quadrilàters cíclics (i en última instància, d'angles inscrits) que els angles oposats d'un quadrilàter sumen 180 °. En conseqüència, en el cas d'un quadrilàter inscrit, θ = 90 °, on el terme
donant la forma bàsica de la fórmula de Brahmagupta.
Teoremes Relacionats[modifica]
- Fórmula d'Heró, per l'àrea d'un triangle.
- Teorema de Pitàgores, per als costats d'un triangle.
- Teorema de Ptolemeu, que relaciona els costats i diagonals d'un quadrilàter cíclic.


































