Filtre IIR
Un filtre IIR[1] (de l'anglès Infinite Impulse Response o Resposta infinita a l'impuls) és un tipus de filtre digital en el qual, com el seu nom indica, si l'entrada és un senyal impuls, la sortida tindrà un nombre infinit de termes no nuls, és a dir, mai torna al repòs.[2]
Els filtres IIR es poden implementar ja sigui com a filtres analògics o digitals. En els filtres digitals IIR, la retroalimentació de sortida és evident en les equacions que defineixen el resultat. S'ha de tenir en compte que a diferència dels filtres FIR, en el disseny de filtres IIR cal considerar acuradament el "temps zero", cas en què les sortides del filtre encara no han estat clarament definides.
Els filtres IIR també solen ser anomenats filtres recursius, ja que la sortida del filtre depèn de valors passats de si mateixa. Exemples de filtres IIR serien el filtre de Txebixev, el filtre Butterworth i el filtre Bessel.
Expressió matemàtica dels filtres IIR[modifica]
La sortida dels filtres IIR depèn de les entrades actuals i passades, i de les sortides en instants anteriors. Això s'aconsegueix mitjançant l'ús de realimentació de la sortida.
On els a i b són els coeficients del filtre. L'ordre és el màxim entre els valors de M i N.
Aplicant la transformada Z a l'expressió anterior:
La funció de transferencia ens permet jutjar si un sistema és o no limitat d'entrada i sortida (Bounded-Input, Bounded-Output; BIBO) estable. Per ser específics, el criteri d'estabilitat BIBO requereix que la ROC (Radium Of Convergence en anglès o Regió de Convergència) del sistema tingui inclòs el cercle unitari. Per exemple, per a un sistema casual, tots els pols de la funció de transferència han de tenir un valor absolut més petit que 1. En altre s paraules, tots els pols han d'estar localitzats dins el cercle unitari del pla Z.
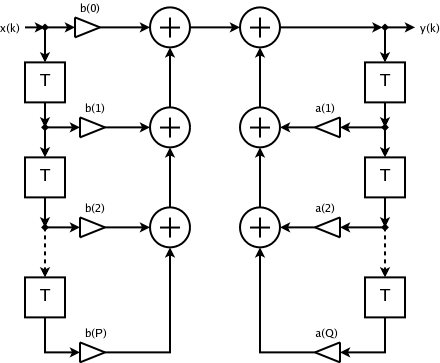
Estructura[modifica]
Hi ha nombroses formes d'implementar els filtres IIR. L'estructura afecta les característiques finals que presentarà el filtre com l'estabilitat. Altres paràmetres a tenir en compte a l'hora de triar una estructura és la despesa computacional que presenta.
Pols i zeros[modifica]
Aquest tipus de filtres presenta pols i zeros que determina l'estabilitat i la causalitat del sistema.
Quan tots els zeros i pols són a l'interior de la circumferència unitat es diu que és fase mínima i el sistema és estable i causal. Si tots els zeros estan a l'exterior és fase màxima.
Si algun pol està fora de la circumferència unitat el sistema és inestable.
Disseny de filtres IIR[modifica]
Les formes habituals de dissenyar aquest tipus de filtres són:
- Indirecta (a partir de prototips analògics)
- Impuls invariant
- Aproximació de derivada s
- Transformació bilineal
- Directa
- Aproximació de Padé
- Aproximació de mínims quadrats
Característiques[modifica]
Les principals diferències respecte als filtres FIR és que els IIR poden complir les mateixes exigències que els anteriors però amb menys ordre de filtre. Això és important a l'hora d'implementar el filtre, ja que presenta una menor càrrega computacional. Una altra característica important seria que disposa d'una millor atenuació respecte als filtres FIR. Aquest tipus de filtres poden ser inestables (oscil·lacions de cicle límit), tot i que es dissenyen per ser estables. En principi no es poden dissenyar per tenir fase lineal però s'hi poden aplicar algunes tècniques com el filtratge bidireccional per aconseguir-ho.
Exemple[modifica]
Suposem que la funció de transferència d'un filtre H és
- amb ROC i
que té un pol a a, és estable i causal. El domini en el temps del temps de resposta és
que és diferent de zero per .
Referències[modifica]
- ↑ UPCTERM,[Enllaç no actiu] Terminologia Tècnica Multilingüe. UPC
- ↑ «Filtro digital IIR» (en castellà). Arxivat de l'original el 2019-05-03. [Consulta: 3 maig 2019].
Vegeu també[modifica]
- Filtre digital
- Filtre FIR
- Matlab
- LabVIEW Digital Filter Design Toolkit
- Processament de senyals digitals







