Nombres de Catalan

n	$C_{n}\,$
0	1
1	1
2	2
3	5
4	14
5	42
6	132
7	429
8	1.430
9	4.862
10	16.796
11	58.786
12	208.012
13	742.900
14	2.674.440
15	9.694.845
16	35.357.670
17	129.644.790
18	477.638.700
19	1.767.263.190
20	6.564.120.420
21	24.466.267.020
22	91.482.563.640
23	343.059.613.650
24	1.289.904.147.324
25	4.861.946.401.452

En combinatòria, els nombres de Catalan formen una seqüència de nombres naturals que apareix en diversos problemes de recompte que habitualment són recursius. Obtenen el seu nom del matemàtic belga Eugène Charles Catalan (1814-1894).

L' n -èsim nombre de Catalan s'obté, aplicant coeficients binomials, a partir de la següent fórmula:

C_{n}={\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{(n+1)!\,n!}}\qquad {\mbox{amb }}n\geq 0.

Propietats[modifica]

Una expressió alternativa per C_n és

C_{n}={2n \choose n}-{2n \choose n-1}\quad {\mbox{amb }}n\geq 1.

Aquesta altra expressió mostra que C _n és un nombre natural, la qual cosa no resulta òbvia a priori mirant la primera fórmula donada.

Els nombres de Catalan satisfan la següent relació de recurrència:

C_{0}=1\quad {\mbox{i}}\quad C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{n-i}\quad {\mbox{amb }}n\geq 0.

I també satisfan:

C_{0}=1\quad {\mbox{i}}\quad C_{n+1}={\frac {2(2n+1)}{n+2}}C_{n},

que pot ésser una forma més eficient de calcular-los.

L'expressió en forma de recursió, seria:

C_{n}={\begin{cases}{\mbox{si }}n=0&\Rightarrow 1\\{\mbox{si }}n>0&\Rightarrow {\cfrac {2(2n-1)}{n+1}}\,C_{n-1}\end{cases}}

Asimptòticament, els nombres de Catalan creixen com:

C_{n}\sim {\frac {4^{n}}{n^{3/2}{\sqrt {\pi }}}}

considerant que el quocient entre l' n -èsim nombre de Català i l'expressió de la dreta tendeix cap 1 quan n → ∞ (això es pot provar fent ús de la fórmula de Stirling).

Aplicacions en combinatòria[modifica]

Hi ha múltiples problemes de combinatòria on la solució la donen els nombres de Catalan. El llibre Enumerative Combinatorics: Volume 2 de Richard P. Stanley conté un conjunt d'exercicis que descriuen 66 interpretacions diferents dels nombres de Catalan. Aquí es mostren alguns exemples, amb il·lustracions per al cas C₃ = 5.

C_n és el nombre de paraules de Dyck de longitud 2n. Una paraula de Dyck és una cadena de caràcters que consisteix en n X's i n Y's de manera que no hi hagi cap segment inicial que tingui més Y's que X's. Per exemple, el següent són les paraules de Dyck de longitud 6:

XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY

Reinterpretar el símbol X com un parèntesi obert i la Y com un parèntesi tancat, C_n compta el nombre d'expressions que contenen n parells de parèntesis correctament col·locats:

((())) ()(()) ()()() (())() (()())

C_n és el nombre de formes diferents d'agrupar n+1 factors mitjançant parèntesis (o el nombre de formes d'associar n aplicacions d'un operador binari). Per n = 3 per exemple, tenim les següents cinc formes diferents d'agrupar els quatre factors:

((ab)c)d\quad (a(bc))d\quad (ab)(cd)\quad a((bc)d)\quad a(b(cd))

Les aplicacions successives d'un operador binari es poden representar amb un arbre binari. En aquest cas, C_n és el nombre d'arbres binaris d'n+1 fulles, en els quals cada node té zero o dos fills:

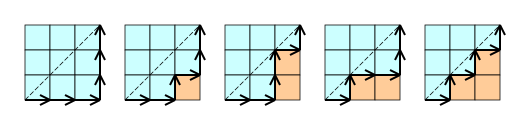
C_n és el nombre de camins monòtons que es poden traçar a través de les línies d'una malla de n × n cel quadrades, de manera que mai es creuï la diagonal. Un camí monòton és aquell que comença a la cantonada inferior esquerra i acaba a la part superior dreta, i consisteix únicament en trams que apunten cap amunt o cap a la dreta. El recompte d'aquests camins és equivalent a comptar paraules de Dyck: X significa "moure's a la dreta" i Y significa "moure's amunt". Els següents diagrames mostren el cas n = 3:

C_n és el nombre de formes diferents de tallar un polígon convex d' n +2 costats a triangles connectant vèrtexs amb línies rectes sense que cap es talli. La següent figura il·lustra el cas dels polígons de 5 costats, quan n = 3:

Enllaços externs[modifica]

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Nombres de Catalan

OEIS successió A000108 (nombres de Catalan)