Resistència de materials
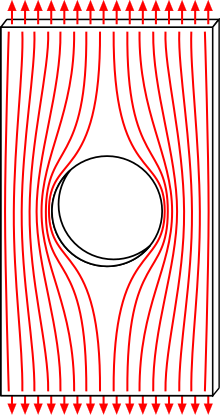
La resistència de materials és una disciplina que tracta el comportament dels objectes sota l'acció de tensions i deformacions. S'estudien els mètodes per calcular tensions en membres estructurals (com bigues, columnes, etc.) i, d'aquesta manera, poder predir com es comportarà l'estructura sota càrregues i com serà de susceptible a fallar tenint en compte les propietats del material.
Un model de resistència de materials estableix una relació entre les forces aplicades, també anomenades càrregues o accions, i els esforços i desplaçaments induïts per elles. Generalment, les simplificacions geomètriques i les restriccions imposades sobre el mode d'aplicació de les càrregues fan que el camp de deformacions i tensions siguin senzills de calcular.
Pel disseny mecànic d'elements amb geometries complicades, la resistència de materials sol ser abundant i cal utilitzar tècniques basades en la teoria de l'elasticitat o la mecànica de sòlids deformables més generals. Aquests problemes plantejats en termes de tensions i deformacions poden llavors ser resolts de forma molt aproximada amb mètodes numèrics com l'anàlisi per elements finits.
Definicions[modifica]
En ciència de materials, la resistència d'un material és la seva capacitat d'aguantar una tensió aplicada sense fallar. Una càrrega aplicada sobre un membre mecànic induirà forces internes dins seu (anomenades tensions), que poden provocar-li deformacions. La tensió aplicada pot ser de tracció, de compressió o tallant.
Tipus de càrregues[modifica]
- Càrrega transversal: força aplicada perpendicularment a l'eix longitudinal de l'element. Aquesta càrrega causa la flexió del membre i es produeixen tensions internes de tracció i compressió.[1] També s'indueixen forces tallants.
- Càrrega axial: força aplicada colinealment a l'eix longitudinal de l'element, el qual s'allarga o es comprimeix (no hi ha flexió).[2]
- Càrrega de torsió: acció de gir causada per un parell de forces extern aplicat sobre un element que té un dels dos extrems fixat.
Tensions[modifica]

La tensió uniaxial s'expressa així:
On F és la força [N] que actua sobre una àrea A [m²].[3] Aquesta àrea pot ser sense deformar o deformada.
- La tensió de compressió és l'estat de tensions causat per una càrrega aplicada que actua intentant reduir la llargada del material al llarg de l'eix on s'aplica dita càrrega. Un cas simple de compressió és la compressió uniaxial, causada per l'acció de dues forces oposades. La resistència a compressió dels materials sol ser més elevada que la seva resistència a tracció; tanmateix, les estructures sotmeses a compressió són més proclius a fallar per teories que depenen de la geometria, com el vinclament.
- La tensió de tracció és l'estat de tensions causat per una càrrega aplicada que actua intentant allargar el material al llarg de l'eix de la càrrega aplicada. Els materials carregats amb tensions de tracció són susceptibles a les concentracions de tensions que es produeixen en zones amb defectes materials, per exemple. Els materials dúctils (com la majoria de metalls) poden tolerar alguns defectes, mentre que els materials fràgils (com la ceràmica) poden fallar molt abans.
- La tensió tallant és l'estat de tensions causat per forces oposades que actuen en línies paral·leles d'acció a través del material, en altres paraules, és l'estat de tensions causat per les cares del material "lliscant" relativament una a l'altra. Un exemple és el tall de paper amb les tisores[4] o les tensions causades per una càrrega a torsió.
Resistències[modifica]
- El límit de fluència és la tensió mínima que produeix una deformació permanent del material. En alguns materials, com ara aliatges de l'alumini, el punt de fluència és difícil d'identificar, per la qual cosa se sol definir com la tensió necessària per causar un 0,2% de deformació plàstica.[5]
- La resistència a compressió és el límit que pot aguantar l'element a tensió de compressió. Un cop sobrepassat pot fallar per fractura dúctil o per fractura fràgil.
- La resistència a tracció és el límit que pot aguantar l'element a tensió de tracció. Un cop sobrepassat pot fallar per fractura dúctil o per fractura fràgil.
- El límit de fatiga o resistència a fatiga mesura de la resistència d'un material o component sota una càrrega cíclica.[6] Sol ser més difícil de determinar que les mesures de resistència estàtica. La resistència a fatiga es dona en forma d'amplitud o rang de tensions (), normalment amb la mitjana de tensions a zero, juntament amb el nombre de cicles per fallar sota aquesta condició d'estat de tensions.
- La resistència a l'impacte és la capacitat del material per aguantar una càrrega aplicada sobtadament. S'expressa en termes d'energia. Es mesura amb l'assaig d'Izod o amb el de Charpy. La resistència a l'impacte sol veure's afectada pel volum, mòdul d'elasticitat, distribució de forces i límit de fatiga. Vegeu també: resiliència.
Deformacions[modifica]
- La deformació d'un material és el canvi de geometria que pateix quan se li aplica un estat de tensions.[7]
- La deformació unitària és el terme matemàtic que expressa la proporció de deformació que ha sofert l'element (deformació per unitat de longitud).[8]
- La fletxa és un terme que descriu com es flexiona un element estructural quan se li aplica una càrrega.[9]
Relacions tensió-deformació[modifica]

- L'elasticitat és la capacitat d'un material per tornar a la seva forma anterior un cop es deixa d'aplicar l'estat tensional. En molts materials, la relació entre la tensió aplicada i la deformació resultant és directament proporcional (fins a un cert límit). El pendent de la línia recta resultant de representar aquestes dues quantitats és el mòdul d'elasticitat.[10]
- La plasticitat és el contrari de la deformació elàstica. Quan un material es deforma plàsticament (després de superar el seu límit de fluència no pot tornar a la seva forma anterior.
Referències[modifica]
- ↑ Beer & Johnston. Mechanics of Materials. 5a. McGraw Hill, 2006, p. 210. ISBN 978-0-07-352938-7.
- ↑ Beer & Johnston. Mechanics of Materials. 5a. McGraw Hill, 2006, p. 7. ISBN 978-0-07-352938-7.
- ↑ Beer & Johnston. Mechanics of Materials. 5a. McGraw Hill, 2006, p. 5. ISBN 978-0-07-352938-7.
- ↑ Beer & Johnston. Mechanics of Materials. 5a. McGraw Hill, 2006, p. 9–10. ISBN 978-0-07-352938-7.
- ↑ Beer & Johnston. Mechanics of Materials. 5a. McGraw Hill, 2006, p. 52. ISBN 978-0-07-352938-7.
- ↑ Beer & Johnston. Mechanics of Materials. 5a. McGraw Hill, 2006, p. 60. ISBN 978-0-07-352938-7.
- ↑ Beer & Johnston. Mechanics of Materials. 5a. McGraw Hill, 2006, p. 47. ISBN 978-0-07-352938-7.
- ↑ Beer & Johnston. Mechanics of Materials. 5a. McGraw Hill, 2006, p. 49. ISBN 978-0-07-352938-7.
- ↑ R. C. Hibbeler. Structural Analysis. 7. Pearson Prentice Hall, 2009, p. 305. ISBN 978-0-13-602060-8.
- ↑ Beer & Johnston. Mechanics of Materials. 5a. McGraw Hill, 2006, p. 53–56. ISBN 978-0-07-352938-7.
Vegeu també[modifica]
Bibliografia[modifica]
- Timoshenko S., Strength of Materials, 3rd ed., Krieger Publishing Company, 1976, ISBN 0-88275-420-3
- Den Hartog, Jacob P., Strength of Materials, Dover Publications, Inc., 1961, ISBN 0-486-60755-0
- Popov, Egor P., Engineering Mechanics of Solids, Prentice Hall, Englewood Cliffs, N. J., 1990, ISBN 0-13-279258-3
- Monleón Cremades, Salvador, Análisis de vigas, arcos, placas y láminas, Universidad Politécnica de Valencia, 1999, ISBN 84-7721-769-6


