Sistema de coordenades esfèriques

En matemàtiques, el sistema de coordenades esfèriques és un sistema de coordenades que es fa servir per a determinar unívocament cada punt de l'espai de tres dimensions assignant-l'hi tres nombres reals anomenats coordenades: la distància radial entre el punt i un origen fixat, l'angle zenital que es mesura des del semieix positiu z fins a la recta que passa per l'origen i el punt, i l'angle azimutal que es mesura entre el semieix positiu x i la projecció ortogonal al pla x-y d'aquesta mateixa recta.
Notació[modifica]
Hi ha diverses convencions per a representar les tres coordenades. D'acord amb l'Organització Internacional per a l'estandardització (ISO 31-11), la notació és (r, θ, φ) per indicar la distància radial, l'angle zenital i l'angle azimutal respectivament.
Els matemàtics nord-americans, inverteixen la notació dels angles zenital i azimutal i fan servir φ pel zenital i θ per l'azimutal. Hi ha una complicació afegida perquè en alguns textos matemàtics els anomenen així però els escriuen canviant l'ordre escrivint primer l'azimut i després el zenit, però aquesta convenció té orientació negativa i s'hauria d'evitar. La convenció americana té l'avantatge de què és més compatible en el significat de θ amb la notació tradicional per al sistema de coordenades polars en dues dimensions i el sistema de coordenades cilíndriques en tres dimensions, mentre que els sistema ISO té una acceptació més estesa arreu del món. Alguns usuaris del sistema ISO també fan servir φ per notar l'angle en coordenades polars i d'aquesta manera evitar el primer problema (tal com ho fa l'estàndard ISO per a coordenades cilíndriques). Una altra notació fa servir ρ per indicar la distància radial.[1] Abans de fer servir les fórmules i les equacions d'un autor en un treball en què empra les coordenades esfèriques, sempre s'hauria de comprovar quina convenció fa servir en la notació. En aquest article es fa servir la notació ISO.
Definició[modifica]

Les tres coordenades (r, θ, φ) es defineixen com:
- r ≥ 0 és la distància de l'origen al punt P.
- 0 ≤ θ ≤ π és l'angle entre la part positiva de l'eix z i la recta que passa per l'origen i P.
- 0 ≤ φ < 2π és l'angle entre la part positiva de l'eix x-axis i la recta que passa per l'origen i P projectada sobre el pla xy.
φ s'anomena l'azimut, mentre que θ s'anomena el zenit, la colatitud o l'angle polar.
θ i φ deixen de tenir sentit quan r = 0 i φ deixa de tenir sentit quan sin(θ) = 0 (a θ = 0 i a θ = π).
Per traçar un punt conegudes les seves coordenades esfèriques, desplaçar r unitats de longitud des de l'origen al llarg de la part positiva de l'eix z, girar un angle θ al voltant de l'eix y en la direcció positiva de l'eix x i girar un angle φ al voltant de l'eix z en la direcció de la part positiva de l'eix y.
Conversions entre sistemes de coordenades[modifica]
Com que el sistema de coordenades esfèriques només és un dels molts sistemes de coordenades en tres dimensions, hi ha equacions que a partir de les coordenades d'un punt en un sistema esfèric permeten calcular les coordenades del mateix un en cada un dels altres i viceversa.
D'aquest càlcul, o d'aplicar aquestes equacions (compondre les funcions) a les equacions que defineixen diferents entitats geomètriques, se'n diu canvi de coordenades o transformació de coordenades.
Sistema de coordenades cartesianes[modifica]
Les tres coordenades esfèriques s'obtenen a partir de les coordenades cartesianes aplicant:
Fixeu-vos que la funció arctangent s'ha de definir de forma adequada de manera que tingui en compte el quadrant correcte de . La funció atan2, o un altre d'equivalent, pot servir per a fer això a efectes de càlcul amb programes informàtics.
A la inversa, Les coordenades cartesianes es poden calcular a partir de les coordenades esfèriques aplicant:
Sistema de coordenades geogràfic[modifica]
El sistema de coordenades geogràfiques és una versió alternativa del sistema de coordenades esfèriques, es va fer servir inicialment en geografia i després també en aplicacions en física i en matemàtiques. En geografia, habitualment es descarta, ρ o se substitueix per un valor que representa l'elevació o altitud.
La latitud és el complement de l'angle zenital i es pot convertir aplicant:
- , o
- ,
Tot i que la latitud també s'escriu habitualment per θ. Aquí representa l'angle zenital mesurat a partir del pla xy amb un domini de -90° ≤ θ ≤ 90°. La longitud es mesura en graus est o oest a partir de 0°, per tant el seu domini és -180° ≤ φ ≤ 180°.
Sistema de coordenades cilíndriques[modifica]
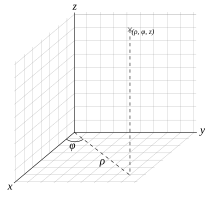
El sistema de coordenades cilíndriques és un sistema de coordenades en tres dimensions que s'obté arrossegant al llarg d'una línia recta perpendicular al pla (l'eix z) el sistema de coordenades polars, la coordenada z descriu l'alçada del punt per damunt (valors positius) o per davall (valors negatius) del pla xy. Les tres coordenades són (ρ, φ, z).
Les coordenades cilíndriques es poden transformar en esfèriques aplicant:
Les coordenades esfèriques es poden transformar en cilíndriques aplicant:
Aplicacions[modifica]
El sistema de coordenades geogràfiques fa servir els dos angles del sistema de coordenades esfèriques per indicar posicions en la superfície de la Terra, d'aquests angles se'n diu latitud i longitud. Igual com el sistema bidimensional de coordenades cartesianes és útil en el pla, el sistema bidimensional de coordenades esfèriques és útil en la superfície d'una esfera. Si en aquest sistema s'agafa om a unitat de mesura de les longituds el radi de l'esfera, llavors la coordenada radial val sempre 1 i en general es pot ignorar. Aquesta simplificació pot ser també molt útil en tractar objectes com ara les matriu de rotació.
Els sistemes de coordenades esfèriques són útils quan s'analitzen sistemes que són simètrics respecte d'un punt; una esfera que en coordenades cartesianes té l'equació x² + y² + z² = c² en coordenades esfèriques, la seva equació és tan simple com r = c. Un exemple és al resoldre una integral triple sobre un domini esfèric.
L'element de superfície per una superfície esfèrica és
L'element de volum és
Les coordenades esfèriques són les coordenades naturals per descriure i analitzar situacions físiques on hi ha simetria esfèrica, com ara el camp d'energia potencial que envolta una esfera (o un punt) amb massa o càrrega. Dies equacions diferencials en derivades parcials importants, l'equació de Laplace i l'equació de Helmholtz, admeten una solució per separació de variables en coordenades esfèriques. Les parts angulars de les solucions d'aquestes equacions prenen la forma d'harmònics esfèrics.
Una altra aplicació és en disseny per a l'ergonomia, on r és la longitud del braç d'una persona quieta i els angles descriuen la direcció del braç per abastar els objectes.
Aplicació en cinemàtica[modifica]
En coordenades esfèriques la posició d'un punt s'escriu,
Llavors la seva velocitat és,
I la seva acceleració és,
Generalització[modifica]
El concepte de coordenades esfèriques es pot estendre a espais de dimensió superior i llavors es parla de coordenades hiperesfèriques.
Notes[modifica]
- ↑ Eric W. Weisstein. «Spherical Coordinates». MathWorld, 26-10-2005. [Consulta: 10 abril 2007].
Vegeu també[modifica]
- Camps vectorials en coordenades cilíndriques i esfèriques
- Laplaciana en coordenades cilíndriques i esfèriques
- Llista de transformacions canòniques de coordenades
- Esfera
- Hiperesfera
Bibliografia[modifica]
- Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. Nova York: McGraw-Hill, 1953, p. 658. ISBN 0-07-043316-X,. LCCN 52-0-11515.
- Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. Nova York: D. van Nostrand, 1956, pp. 177–178. LCCN 55-0-10911.
- Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. Nova York: McGraw-Hill, 1961, pp. 174–175. LCCN 59-0-14456, ASIN B0000CKZX7.
- Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. Nova York: Springer Verlag, 1967, pp. 95–96. LCCN 67-0-25285.
- Moon P, Spencer DE. «Spherical Coordinates (r, θ, ψ)». A: Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions. corrected 2nd ed., 3rd print ed.. Nova York: Springer-Verlag, 1988, pp. 24–27 (Table 1.05). ISBN 978-0387184302.
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Sistema de coordenades esfèriques |























