Successió de Farey
En matemàtiques, la seqüència de Farey o successió de Farey d'ordre n és la seqüència de les fraccions irreductibles entre 0 i 1, o sense aquesta restricció,[Nota 1] en la qual el denominador és inferior o igual a n i en ordre creixent.
-
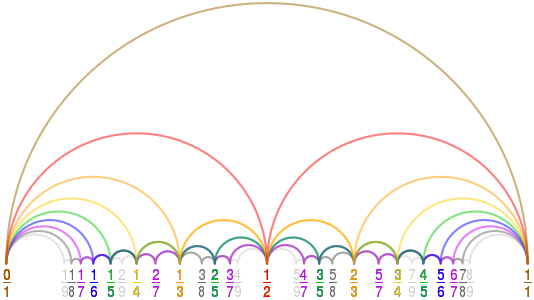
Diagrama de Farey a F9 representat amb arcs circulars. A la imatge SVG, passeu el cursor per sobre d'una corba per ressaltar-la i els seus termes.
-
Diagrama de Farey a F9
Qualsevol successió comença amb el valor 0, representat per la fracció 0⁄1, i finalitza amb el valor 1, representat per la fracció 1⁄1 (tot i que certs autors ometen aquest terme).
-
Patró simètric fet pels denominadors de la seqüència de Farey, F9
De vegades aquesta successió rep el nom de sèrie de Farey, però això no és estrictament correcte atès que els termes no se sumen.
-
Patró simètric fet pels denominadors de la seqüència de Farey, F25
Porta el nom del seu inventor, el geòleg anglès John Farey (1766-1826). El 1924, el matemàtic suís Jérôme Franel, va trobar una subtil relació entre la sèrie de Farey i la Hipòtesi de Riemann, cosa que va fer que Edmund Landau investigués aquesta relació, publicant un parell d'articles sobre el tema.[1][2]
Exemples[modifica]
Les seqüències de Farey d'ordres de l'1 al 8 són:
- F1 = { 01, 11 }
- F₂ = { 01, 12, 11 }
- F₃ = { 01, 13, 12, 23, 11 }
- F4 = { 01, 14, 13, 12, 23, 34, 11 }
- F5 = { 01, 15, 14, 13, 25, 12, 35, 23, 34, 45, 11 }
- F6 = { 01, 16, 15, 14, 13, 25, 12, 35, 23, 34, 45, 56, 11 }
- F7 = { 01, 17, 16, 15, 14, 27, 13, 25, 37, 12, 47, 35, 23, 57, 34, 45, 56, 67, 11 }
- F8 = { 01, 18, 17, 16, 15, 14, 27, 13, 38, 25, 37, 12, 47, 35, 58, 23, 57, 34, 45, 56, 67, 78, 11 }
| Centrat |
|---|
| F1 = { 01, 11 } |
| F₂ = { 01, 12, 11 } |
| F₃ = { 01, 13, 12, 23, 11 } |
| F4 = { 01, 14, 13, 12, 23, 34, 11 } |
| F5 = { 01, 15, 14, 13, 25, 12, 35, 23, 34, 45, 11 } |
| F6 = { 01, 16, 15, 14, 13, 25, 12, 35, 23, 34, 45, 56, 11 } |
| F7 = { 01, 17, 16, 15, 14, 27, 13, 25, 37, 12, 47, 35, 23, 57, 34, 45, 56, 67, 11 } |
| F8 = { 01, 18, 17, 16, 15, 14, 27, 13, 38, 25, 37, 12, 47, 35, 58, 23, 57, 34, 45, 56, 67, 78, 11 } |
| Ordenat |
|---|
F1 = {0/1, 1/1}
F2 = {0/1, 1/2, 1/1}
F3 = {0/1, 1/3, 1/2, 2/3, 1/1}
F4 = {0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1}
F5 = {0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1}
F6 = {0/1, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 1/1}
F7 = {0/1, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 2/5, 3/7, 1/2, 4/7, 3/5, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 1/1}
F8 = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}
|
Gràfica «esclat solar» de Farey[modifica]
Traçant els numeradors en funció dels denominadors d'una seqüència de Farey s'obté una forma com els gràfics inferiors.
-
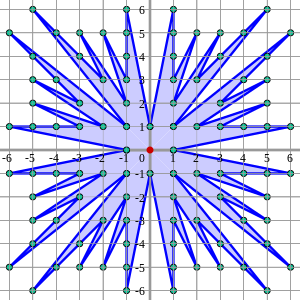
Gràfica «esclat solar» de Farey d'ordre 6, amb 1 interior (vermell) i 96 punts de límit (verd) donant una àrea d'1 + 96/2 − 1 = 48, segons el teorema de Pick
-
Iteracions 1-10
En reflectir aquesta forma al voltant dels eixos diagonal i principal es genera la gràfica «esclat solar» de Farey. L'esclat solar Farey d'ordre n connecta els punts de la quadrícula d'enters visibles des de l'origen al quadrat del costat 2n, centrats a l'origen. Utilitzant el teorema de Pick, l'àrea de l'esclat solar és 4(|Fn|−1), on |Fn| és el nombre de fraccions en Fn.
Història[modifica]
| « | La història de les sèries de Farey és molt curiosa | » |
| — [Hardy, Wright 1979] | ||
| « | ... una vegada més, l'home el nom del qual es va donar a una relació matemàtica no va ser el descobridor original pel que fa als registres. | » |
| — [Beiler 1964, p. XVI] | ||
Les seqüències de Farey reben el nom del geòleg britànic John Farey, Sr., la carta del qual sobre aquestes seqüències es va publicar a la revista Philosophical Magazine el 1816.[3] Farey va conjecturar, sense oferir proves, que cada nou terme en una expansió de la seqüència de Farey és el mediant dels seus veïns. Cauchy va llegir la carta de Farey, que va aportar una prova en els seus Exercices de mathématique, i va atribuir aquest resultat a Farey.
De fet, un altre matemàtic, Charles Haros, havia publicat resultats similars el 1802 que no eren coneguts ni per Farey ni per Cauchy.[4] Així, va ser un accident històric el que va vincular el nom de Farey amb aquestes seqüències. Aquest és un exemple de la Llei de Stigler.
Propietats[modifica]
-
Diagrama de Farey amb cercles, ordre F4
-
Diagrama de Farey amb cercles, ordre F6
Longitud de la seqüència i índex d'una fracció[modifica]
La seqüència de Farey d'ordre n conté tots els membres de les seqüències de Farey d'ordre inferior. En particular Fn conté tots els membres de Fn−1 i també conté una fracció addicional per a cada nombre que sigui menor que n i coprimer a n. Així F6 està format per F5 juntament amb les fraccions 16 i 56.
El terme mig d'una seqüència de Farey Fn és sempre 12, per a n > 1. A partir d'això, podem relacionar les longituds de Fn i Fn−1 utilitzant la funció φ d'Euler :
Utilitzant el fet que |F1| = 2, podem derivar una expressió per a la longitud de Fn:[5]
on és la suma indicatriu.
També tenim:
i mitjançant una fórmula d'inversió de Möbius:
on µ(d) és el nombre teòric de la funció de Möbius, i és la funció de part entera.
El comportament asimptòtic de |Fn| és:
L'índex d'una fracció en la seqüència de Farey és simplement la posició que ocupa en la seqüència. Això és d'especial rellevància, ja que s'utilitza en una formulació alternativa de la hipòtesi de Riemann (vegeu més avall). A continuació es mostren diverses propietats útils:
L'índex d' on i és el mínim comú múltiple del primer nombre, , ve donat per:[6]
Termes veïns de Farey[modifica]
Les fraccions que són termes veïns en qualsevol seqüència de Farey es coneixen com a parell de Farey i tenen les propietats següents:
Si ab i cd són veïns en una seqüència de Farey, amb ab < cd, llavors la seva diferència cd − ab és igual a 1bd. Això es deu al fet que cada parell consecutiu de racionals de Farey té una àrea equivalent a 1.[7]
Si r1=p/q i r₂=p'/q' s'interpreten com a vectors (p,q) en el pla x,y, l'àrea de A(p/q,p'/q') està donat per qp' - q'p. Com que qualsevol fracció afegida entre dues fraccions de seqüències de Farey consecutives anteriors es calcula com a mediant (⊕)
A(r1,r1⊕r₂) = A(r1,r1) + A(r1,r₂) = A(r1,r₂) = 1 (a partir de r1=1/0 i r₂=0/1 la seva àrea ha de ser 1).
Des de:
això equival a dir això
- .
Així 13 i 25 són veïns F5, i la seva diferència és 115.
El contrari també és cert. Si
per a nombres enters positius a,b,c i d amb a < b i c < d llavors ab i cd seran els veïns de la seqüència d'ordre Farey max(b,d).
Si pq és veí de ab i cd en alguna seqüència de Farey, amb
llavors pq és la fracció mediant de ab i cd ; en altres paraules,
Això es desprèn fàcilment de la propietat anterior, ja que si bp – aq = qc – pd = 1, llavors bp + pd = qc + aq, p(b + d) = q(a + c), pq = a + cb + d.
Es dedueix que si ab i cd són veïns d'una seqüència de Farey, llavors el primer terme que apareix entre ells a mesura que s'incrementa l'ordre de la seqüència de Farey és
que apareix per primera vegada a la seqüència de Farey d'ordre b + d.
Així el primer terme que apareix entre 13 i 25 és 38, que apareix a F8.
El nombre total de parelles de veïns de Farey Fn és 2|Fn|-3.
L'arbre Stern-Brocot és una estructura de dades que mostra com es construeix la seqüència 0 (= 01) i 1 (= 11), prenent mediants successius.
Veïns de Farey i fraccions contínues[modifica]
Les fraccions que apareixen com a veïnes en una seqüència de Farey tenen expansions de fraccions contínues estretament relacionades. Cada fracció té dues expansions de fraccions contínues: en una, el terme final és 1; en l'altre el termini final és superior a 1. Si pq, que apareix per primera vegada a la seqüència de Farey Fq, té expansions de fraccions contínues
- [0; a1, a₂, ..., an − 1, an, 1]
- [0; a1, a₂, ..., an − 1, an + 1]
llavors el veí més proper de pq en Fq (que serà el seu veí amb el denominador més gran) té una expansió de fracció contínua
- [0; a1, a₂, ..., an]
i el seu altre veí té una expansió continuada de fraccions
- [0; a1, a₂, ..., an − 1]
Per exemple, 38 té les dues expansions de fraccions contínues [0; 2, 1, 1, 1] i [0; 2, 1, 2], i els seus veí en F8 és 25, que es pot ampliar com [0; 2, 1, 1]; i 13, que es pot ampliar com [0; 2, 1].
Fraccions de Farey i el mínim comú múltiple[modifica]
El mcm es pot expressar com els productes de les fraccions de Farey com
on és la segona funció de Chebyshev.[8][9]
Fraccions de Farey i màxim comú divisor[modifica]
Com que la funció φ d'Euler està directament connectada amb el mcd, també ho és el nombre d'elements a Fn.
Per a tres fraccions de Farey qualsevol ab, cd i ef la següent identitat entre els mcd dels determinants de la matriu 2x2 en valor absolut es compleix:[10]
Aplicacions[modifica]
Les seqüències de Farey són molt útils per trobar aproximacions racionals de nombres irracionals.[11] Per exemple, la construcció per Eliahou[12] d'un límit inferior de la durada dels cicles no trivials en el procés 3x+1 utilitza seqüències de Farey per calcular una expansió de fracció contínua del nombre log₂(3).
En sistemes físics amb fenòmens de ressonància, les seqüències de Farey proporcionen un mètode molt elegant i eficient per calcular ubicacions de ressonància en 1D[13] i 2D.[14]
Les seqüències de Farey són destacades en els estudis de planificació de camins de qualsevol angle en quadrícules de cel·les quadrades, per exemple en caracteritzar la seva complexitat computacional[15] o optimitat.[16] La connexió es pot considerar en termes de camins r-restringits, és a dir, camins formats per segments de línia que travessen cadascun com a màxim files i com a màxim columnes de cel·les. Sigui el conjunt de vectors tal que , , i , són coprimers. Sigui el resultat del reflex en la línea . Sigui . Aleshores, qualsevol camí r-restringit per r es pot descriure com una seqüència de vectors a partir de . Hi ha una bijecció entre i la seqüència de Farey d'ordre donat per mapejat a .
Per a cercles de Ford[modifica]
Hi ha una connexió entre la seqüència de Farey i els cercles de Ford.
Per cada fracció pq (en els seus termes més baixos) hi ha un cercle de Ford C[pq], que és el cercle amb radi 1/(2q2) i el centre a (pq, 1 2q² ). Dos cercles de Ford per a diferents fraccions són disjunts o tangents entre si; dos cercles de Ford mai es tallen. Si 0 < pq < 1 llavors els cercles de Ford que són tangents a C[pq] són precisament els cercles de Ford per a les fraccions que són veïnes de pq en alguna seqüència de Farey.
-
Comparació de cercles de Ford i un diagrama de Farey amb arcs circulars per a n d'1 a 9. Cada arc talla els seus cercles corresponents en angle recte. A la imatge SVG, passeu el cursor per sobre d'un cercle o una corba per ressaltar-lo i els seus termes
-
Tamís d'Apol·loni (0,0,1,1) i el diagrama de ressonància de Farey
Així C[25] és tangent a C[12], C[13], C[37], C[38] etc.
Els cercles de Ford també apareixen al tamís d'Apol·loni (0,0,1,1). La imatge superior ho il·lustra juntament amb les línies de ressonància de Farey.[10]
Hipòtesi de Riemann[modifica]
Les seqüències de Farey s'utilitzen en dues formulacions equivalents de la hipòtesi de Riemann. Suposem els termes de són . Definim , el altres paraules és la diferència entre el terme k-èssim de l'enèsima seqüència de Farey i el k-è membre d'un conjunt del mateix nombre de punts, distribuïts uniformement en l'interval unitari. El 1924 Jérôme Franel va demostrar que la declaració.[17]
és equivalent a la hipòtesi de Riemann, i llavors Edmund Landau va remarcar (just després de l'article de Franel) que l'afirmació[18]
també és equivalent a la hipòtesi de Riemann.
Altres sumes que impliquen fraccions de Farey[modifica]
La suma de totes les fraccions de Farey d'ordre n és la meitat del nombre d'elements:
La suma dels denominadors de la seqüència de Farey és el doble de la suma dels numeradors i es relaciona amb la funció φ d'Euler:
que va ser conjecturada per Harold L. Aaron el 1962 i demostrada per Jean A. Blake el 1966. Una prova d'una línia de la conjectura de Harold L. Aaron és la següent.
La suma dels numeradors és . La suma dels denominadors és . El quocient de la primera suma per la segona suma és .
Siguin bj els denominadors ordenats de Fn, llavors:[19]
i
Siguin aj/bj la j-ena fraccion de Farey en Fn, llavors
que es demostra a [Hall, Shiu 2003, p. 2009-223].[20] També segons aquesta referència el terme dins de la suma es pot expressar de moltes maneres diferents:
obtenint així moltes sumes diferents sobre els elements de Farey amb el mateix resultat. Utilitzant la simetria al voltant de 1/2, la suma anterior es pot limitar a la meitat de la seqüència com
La funció de Mertens es pot expressar com una suma sobre fraccions de Farey com
- on és la seqüència de Farey d'ordre n.
Aquesta fórmula s'utilitza en la demostració del teorema de Franel-Landau.[21]
El terme següent[modifica]
Existeix un algorisme sorprenentment senzill per generar els termes de Fn en ordre tradicional (creixent) o en ordre no tradicional (descendent). L'algorisme calcula cada entrada successiva en termes de les dues entrades anteriors utilitzant la propietat mediant donada anteriorment. Si ab i cd són les dues entrades donades, i pq és la següent entrada desconeguda, llavors cd = a + pb + q. A partir de cd és en termes més baixos, ha d'haver un nombre enter k tal que kc = a + p i kd = b + q, donant p = kc − a i q = kd − b. Si considerem que p i q són funcions de k, aleshores
per tant, com més gran és k, més a prop pq arriba a cd.
Per donar el següent terme de la seqüència, k ha de ser el més gran possible, subjecte a kd − b ≤ n (ja que només estem considerant nombres amb denominadors no superiors a n), de manera que k és el nombre enter més gran ≤n + bd. Si tornem a posar aquest valor de k a les equacions de p i q, s'obté
Això s'implementa a Python de la següent manera:
def farey_sequence(n: int, descending: bool = False) -> None:
"""Imprimeix la seqüència enèima de Farey. Permet pujar o baixar."""
(a, b, c, d) = (0, 1, 1, n)
if descending:
(a, c) = (1, n - 1)
print("{0}/{1}".format(a, b))
while (c <= n and not descending) or (a > 0 and descending):
k = (n + b) // d
(a, b, c, d) = (c, d, k * c - a, k * d - b)
print("{0}/{1}".format(a, b))
Les cerques de força bruta per a solucions d'equacions diofàntiques en racionals sovint poden aprofitar la sèrie de Farey (per cercar només formes reduïdes). Les línies marcades amb (*) també es poden modificar per incloure dos termes adjacents qualsevol per generar termes només més grans (o més petits) que un terme determinat.[22]
Notes[modifica]
- ↑ La seqüència de totes les fraccions reduïdes amb denominadors no superiors a n, enumerades per ordre de la seva mida, s'anomena seqüència de Farey d'ordre n. Amb el comentari: «Aquesta definició de les seqüències de Farey sembla ser la més convenient. Tanmateix, alguns autors prefereixen restringir les fraccions a l'interval de 0 a 1» — [Niven, Zuckerman 1972, p. Definició 6.1]
Referències[modifica]
- ↑ Alexanderson, 2000, p. 42.
- ↑ Guthery, 2001, p. 7.
- ↑ Philosophical Magazine, vol. 47, 1816, pàg. 385-386.
- ↑ Beiler, 1964, p. XVI.
- ↑ Sloane, N. J. A. «Sequence A005728» (en anglès). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ 6,0 6,1 Tomás García, 2022.
- ↑ Austin, 2008.
- ↑ Martin, 2009.
- ↑ Wehmeier, 2009.
- ↑ 10,0 10,1 Tomás García, 2020.
- ↑ «Farey Approximation» (en anglès). NRICH. Arxivat de l'original el 2018-11-19. [Consulta: 14 maig 2023].
- ↑ Eliahou, 1993, p. 45-56.
- ↑ Zhenhua i Harter, 2015, p. 208-213.
- ↑ Tomás García, 2014, p. 014001.
- ↑ Harabor, Daniel Damir; Grastien, Alban; Öz, Dindar; Aksakalli, Vural «Optimal Any-Angle Pathfinding In Practice» (en anglès). Journal of Artificial Intelligence Research, 56, 26-05-2016, pàg. 89-118. DOI: 10.1613/jair.5007.
- ↑ Hew, Patrick Chisan «The Length of Shortest Vertex Paths in Binary Occupancy Grids Compared to Shortest r-Constrained Ones» (en anglès). Journal of Artificial Intelligence Research, 59, 19-08-2017, pàg. 543–563. DOI: 10.1613/jair.5442.
- ↑ Franel, 1924, p. 198-201.
- ↑ Landau, 1921, p. 202-206.
- ↑ Girstmair, 2010, p. 72-78.
- ↑ Hall i Shiu, 2003, p. 209-223.
- ↑ Edwards, 1974, p. 263-267.
- ↑ Routledge, 2008, p. 55-62.
Bibliografia[modifica]
- Alexanderson, Gerald L. The Random Walks of George Polya (en anglès). The Mathematical Association of America, 2000.
- Austin, David «Trees, Teeth, and Time: The mathematics of clock making» (en anglès). American Mathematical Society [Rhode Island], desembre 2008. Arxivat de l'original el 2020-02-04 [Consulta: 14 maig 2023].
- Beiler, Albert H. Recreations in the Theory of Numbers (en anglès). Dover, 1964. ISBN 0-486-21096-0.
- Cobeli, Cristian; Zaharescu, Alexandru «The Haros-Farey sequence at two hundred years. A survey» (en anglès). Acta Univ. Apulensis Math. Inform., 5, 2003, pàg. 1-38. (pàgina 1-20
 PDF), (pàgina 21-38
PDF), (pàgina 21-38  PDF)
PDF) - Edwards, Harold M. «Cap. 12.2 Miscellany. The Riemann Hypothesis and Farey Series». A: Riemann's Zeta Function (en anglès). Nova York: Academic Press, 1974 (Pure and Applied Mathematics). ISBN 978-0-08-087373-2. OCLC 316553016.
- Eliahou, Shalom «The 3x+1 problem: new lower bounds on nontrivial cycle lengths» (en anglès). Discrete Mathematics, 118(1)-118(3), agost 1993. DOI: 10.1016/0012-365X(93)90052-U.
- Franel, Jérôme «Les suites de Farey et le problème des nombres premiers» (en francès). Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, 1924.
- Girstmair, Kurt «Farey Sums and Dedekind Sums» (en anglès). The American Mathematical Monthly, 117(1), 2010. DOI: 10.4169/000298910X475005. JSTOR: 10.4169/000298910X475005.
- Graham, Ronald L; Knuth, Donald E; Patashnik, Oren. Concrete Mathematics: A foundation for computer science (en anglès). Boston, MA: Addison-Wesley, 1989, p. 115-123, 133-139, 150, 462-463, 523-524. ISBN 0-201-55802-5. En particular, vegeu §4.5 (p. 115-123), Problema extra 4.61 (p. 150, 523-524), §4.9 (p. 133-139), §9.3, Problema 9.3.6 (p. 462-463).
- Guthery, Scott B. «Cap 1. The Mediant». A: A Motif of Mathematics: History and Application of the Mediant and the Farey Sequence (en anglès). Boston: Docent Press, 2011. ISBN 978-1-4538-1057-6. OCLC 1031694495.
- Hall, R. R; Shiu, P «The Index of a Farey Sequence» (en anglès). Michigan Math. J., 51(1), 2003. DOI: 10.1307/mmj/1049832901.
- Hardy, G. H; Wright, E. M. «III». A: An Introduction to the Theory of Numbers. Oxford University Press, 1979. ISBN 0-19-853171-0.
- Landau, Edmund «Bemerkungen zu der vorstehenden Abhandlung von Herrn Franel» (en alemany). Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, 1924.
- Martin, Greg. A product of Gamma function values at fractions with the same denominator (en anglès), 2009.
- Matveev, Andrey O. Farey Sequences: Duality and Maps Between Subsequences (en alemany). Berlín: De Gruyter, 2017. ISBN 978-3-11-054662-0.
- Niven, Ivan M; Zuckerman, Herbert S. An Introduction to the Theory of Numbers (en anglès). John Wiley and Sons, 1972.
- Routledge, Norman «Computing Farey series» (en anglès). The Mathematical Gazette, 92(523), març 2008.
- Tomás García, Rogelio «From Farey sequences to resonance diagrams» (en anglès). Physical Review Special Topics - Accelerators and Beams, 17, 2014. DOI: 10.1103/PhysRevSTAB.17.014001.
- Tomás García, Rogelio «Equalities between greatest common divisors involving three coprime pairs» (
 PDF) (en anglès). Notes on Number Theory and Discrete Mathematics, 26(3), agost 2020. DOI: 10.7546/nntdm.2020.26.3.5-7.
PDF) (en anglès). Notes on Number Theory and Discrete Mathematics, 26(3), agost 2020. DOI: 10.7546/nntdm.2020.26.3.5-7. - Tomás García, Rogelio. Imperfections and corrections (en anglès), 2020b.
- Tomás García, Rogelio «Partial Franel sums» (
 PDF) (en anglès). Journal of Integer Sequences, 25(1), gener 2022.
PDF) (en anglès). Journal of Integer Sequences, 25(1), gener 2022. - Wehmeier, Stefan. The LCM(1,2,...,n) as a product of sine values sampled over the points in Farey sequences (en anglès), 2009.
- Zhenhua Li, A; Harter, W. G «Quantum Revivals of Morse Oscillators and Farey-Ford Geometry» (en anglès). Chem. Phys. Lett., 633, 2015. arXiv: 1308.4470. DOI: 10.1016/j.cplett.2015.05.035.
Vegeu també[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Successió de Farey |
Enllaços externs[modifica]
- «Farey series» (en anglès). EMS Press, 2001 [1994].
- OEIS successió A005728 (nombre de fraccions de la sèrie de Farey d'ordre n)
- Vepstas, Linas. «The Minkowski Question Mark, GL(2,Z), and the Modular Group» (
 PDF) (en anglès). Revisa els isomorfismes de l'arbre de Stern-Brocot.
PDF) (en anglès). Revisa els isomorfismes de l'arbre de Stern-Brocot.



























![{\displaystyle n={\rm {mcm}}([2,i])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5312df7ce6b8ad535307f978b4126ae2075894e1)






![{\displaystyle {\text{mcm}}[1,2,...,N]=e^{\psi (N)}={\frac {1}{2}}\left(\prod _{r\in F_{N},0<r\leq 1/2}2\sin(\pi r)\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1005b53d4ea70ebe6ca45351e25d07f931d89496)





































