Teorema de la funció inversa
En matemàtiques, el teorema de la funció inversa és un resultat de geometria diferencial. Indica que si una funció f és contínuament diferenciable en un punt a i aquesta diferencial és contínua i també ho és la seva recíproca, llavors f és localment invertible i la seva inversa és diferenciable.
Aquest teorema és equivalent al de la funció implícita, el seu ús està àmpliament estès. Es fa servir en geometria algebraica, que, sota una forma o una altra es fa servir en les demostracions del teorema de la bola peluda. Indica que sobre una esfera, que suporta en cada punt un vector no nul, la funció que associa a cada punt de l'esfera el vector, conté almenys una discontinuïtat. La conseqüència és que un tokamak no és mai esfèric sinó tòric. Es troba també en certes demostracions de les propietats dels multiplicadors de Lagrange que permeten resoldre problemes d'extrems, com el teorema isoperimétric una de les formes del qual indica que la figura amb més superfície possible en un pla, de perímetre donat, és el cercle. També es fa servir per demostrar el teorema del redreçament, que permet establir que una equació diferencial autònoma del pla que només tingui solucions fitades no pot engendrar el caos, resultat que es coneix amb el nom de teorema de Poincaré-Bendixson.
Per demostrar-lo es fa servir una versió simple del teorema del punt fix. Permet establir el resultat en diversos casos, un espai vectorial real de dimensió finita, un espai de Banach o inclús una varietat diferencial. Hi ha una versió més forta el teorema d'inversió global.
Enunciats[modifica]
Hi ha diverses formes, la que es proposa aquí és relativament general:[1]
- Teorema de la funció inversa: Sigui f una aplicació de U en F, on U és un obert d'un espai de Banach real, F un espai de Banach i x un punt de U. Si f és de classe Cp, amb p estrictament positiu i si el diferencial de f en el punt x és un isomorfisme continu amb el reciproc també continu, llavors existeix un veïnat V de x tal que la restricció de f a V és una bijecció bicontínua en f(V) i la seva recíproca és de classe Cp.
Aquest enunciat necessita algunes explicacions. Un espai de Banach és un espai vectorial normat i complet. Un exemple important és el dels espais vectorials reals de dimensió finita. Certes versions limiten el seu enunciat a aquest cas particular.[2]
El diferencial correspon a la generalització de la noció de derivada. Un creixement f(x + h) - f(x), si h és petit, és gairebé igual a f' (x).h. A priori aquesta igualtat posseeix un sentit si f és una funció de R en R i el terme f'(x) designa la derivada de la funció f en el punt x. Si la funció està definida d'un espai vectorial a un altre, aquest resultat es generalitza però f'(x), que llavors es nota dfx o Dfx, és una aplicació lineal anomenada diferencial de f en el punt x. L'aplicació, que a x li associa Dfx, és l'aplicació diferencial de f, i és una aplicació d'un espai vectorial en un altre, de vegades també es pot diferenciar. Si aquesta operació és factible p vegades, i si el diferencial p-èsim és continu, l'aplicació f s'anomena de classe Cp.
Es té del corol·lari següent:[3]
- Teorema global de la funció inversa: Sota les hipòtesis del teorema precedent, si f és a més injectiva i si per a tot x de U el diferencial Dfx de f en el punt x és un isomorfisme bicontinu, llavors f és una bijecció de U en f(U) i la seva recíproca és de classe Cp.
Observació: Una aplicació bijectiva de classe Cp, tal que la seva recíproca sigui també de classe Cp s'anomena un difeomorfisme de classe Cp.
Enfocament intuïtiu[modifica]
Funcions reals de la variable real[modifica]

El cas de les funcions reals de variable real és una mica particular. Si una funció f definida sobre un interval J és estrictament monòtona (creixent o decreixent), llavors és injectiva, per tant és una bijecció de J en f(J) i admet una recíproca f -1. A més, si és continua, el teorema del valor intermedi demostra que f(J) és també un interval. La gràfica de f -1 és la simètrica de la de f respecte a la primera bisectriu, d'equació x = y, com s'il·lustra a la figura de la dreta.
La continuïtat no és difícil d'establir, sigui y un punt de f(J), x el punt de J tal com f(x) = y i ε un real estrictament positiu. La imatge de l'interval ]x - ε, x + ε[ per la funció f és un interval obert que conté y. És possible trobar un real estrictament positiu μ tal que ]y - μ, y + μ[ estigui inclòs en la imatge de l'interval ]x - ε, x + ε[ per la funció f. El que, en termes matemàtics s'expressa per la proposició:
Aquesta proposició expressa exactament la continuïtat de f -1 en el punt y. L'aplicació f -1 és derivable, si f ho és i la seva derivat no és nul·la. Una presentació freqüent consisteix a derivar la funció f composta amb la seva recíproca.[4] Aquest mètode té l'avantatge de ser elemental, no obstant això és una mica feble mentre no s'hagi demostrat que la funció recíproca és derivable.[Nota 1]
El cas d'una funció real de la variable real és una mica particular. Els resultats són més globals i requereixen hipòtesis més febles. Només amb l'estricta monotonia i amb la continuïtat sobre un interval hi ha prou per demostrar l'existència d'una funció recíproca continua. Amb només la derivabilitat en un punt hi ha prou per establir la derivabilitat de la funció recíproca sobre la imatge d'aquest punt (si la derivada inicial és no nul·la). Però, els mètodes emprats no són generalitzables. Un espai vectorial no disposa d'un ordre en la imatge del conjunt dels nombres reals, d'on sorgeix la necessitat d'hipòtesis més fortes per arribar a un resultat més feble.
Dimensió dos[modifica]
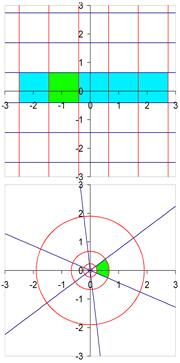
La dimensió dos ja indica l'existència d'un comportament diferent al del paràgraf precedent. S'il·lustra per la funció f de R² en R² definida per:
La figura de l'esquerra indica com es transforma el pla. La imatge de la figura situada a dalt s'il·lustra a sota. El quadrat verd ha estat deformat de manera bijectiva. A partir d'un punt de la imatge del quadrat verd, és possible reconstituir el punt del quadrat d'origen. L'aplicació f satisfà les hipòtesis del teorema de l'article. Per verificar que l'aplicació és localment inversible, és útil determinar el seu diferencial. La seva matriu, anomenada jacobiana és la següent:
 Per saber si el diferencial és un isomorfisme, el més simple és de calcular el seu determinant, anomenat determinant jacobià. És igual a exp(2x) i no és mai nul. L'aplicació és en conseqüència localment inversible en cada punt. A diferència de les funcions diferenciables i definides sobre un interval de R, aquesta propietat no implica el caràcter globalment injectiu de f. Afegir 2.π a la segona coordenada no modifica la imatge per f, així cada punt de R² posseeix una infinitat d'antecedents, a excepció de l'origen que no en té pas. Aquesta funció es pot veure com l'exponencial complexa. La seva recíproca, el logaritme complex no pot ser definit sobre C tot sencer i existeixen diversos mètodes per definir-lo.
Per saber si el diferencial és un isomorfisme, el més simple és de calcular el seu determinant, anomenat determinant jacobià. És igual a exp(2x) i no és mai nul. L'aplicació és en conseqüència localment inversible en cada punt. A diferència de les funcions diferenciables i definides sobre un interval de R, aquesta propietat no implica el caràcter globalment injectiu de f. Afegir 2.π a la segona coordenada no modifica la imatge per f, així cada punt de R² posseeix una infinitat d'antecedents, a excepció de l'origen que no en té pas. Aquesta funció es pot veure com l'exponencial complexa. La seva recíproca, el logaritme complex no pot ser definit sobre C tot sencer i existeixen diversos mètodes per definir-lo.
Un segon exemple ve donat per la següent funció g el determinant jacobià de la qual és igual a x²/2:
Aquest exemple s'il·lustra amb les mateixes convencions a la figura de la dreta. La imatge de la zona blava a l'esquerra es transforma en una espècie de papallona. L'aplicació no és inversible al veïnatge d'un punt que tingui una primera coordenada nul·la. Intuïtivament, es veu que les dues figures blaves no són pas equivalents. Si se suprimeix el punt central a la de dreta, la figura llavors consisteix en dos components connexos. La retirada d'un punt qualsevol de la figura blava de l'esquerra no produeix mai aquest efecte.
Aplicacions[modifica]
 Les aplicacions del teorema de la funció inversa són múltiples i toquen diferents branques de les matemàtiques. Una d'elles concerneix a la branca origen del teorema: la geometria diferencial. Aquesta aplicació es du a la pràctica amb l'ajuda d'un corol·lari que porta el nom de teorema de la funció implícita. Pren la forma d'un resultat equivalent al d'aquest article i el teorema de la funció inversa apareix, o bé sota la seva forma original, o bé sota la de la funció implícita.
Les aplicacions del teorema de la funció inversa són múltiples i toquen diferents branques de les matemàtiques. Una d'elles concerneix a la branca origen del teorema: la geometria diferencial. Aquesta aplicació es du a la pràctica amb l'ajuda d'un corol·lari que porta el nom de teorema de la funció implícita. Pren la forma d'un resultat equivalent al d'aquest article i el teorema de la funció inversa apareix, o bé sota la seva forma original, o bé sota la de la funció implícita.

Sota aquesta forma, se l'utilitza per estudiar les figures geomètriques definides en forma d'equacions, il·lustrades per l'exemple següent:
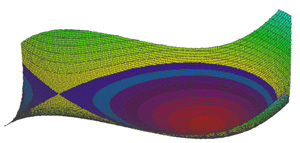
Si el terme de l'esquerra es veu com una funció f de R² amb valors a R, la figura del pla estudiat és la intersecció de la gràfica de la funció f, il·lustrada a la dreta, i del pla de l'equació z = 0. De manera més general, una varietat diferencial correspon a la generalització de corbes o superfícies regulars, en dimensió qualsevol. Existeixen dues maneres de definir-les localment, a través d'una equació, o bé cartesiana, o bé paramètrica. El resultat de l'article mostra l'equivalència d'aquestes dues maneres.
En càlcul diferencial, els multiplicadors de Lagrange permeten trobar extrems sota restriccions. Si U és un obert d'un espai euclidià, l'objectiu és de trobar un extrem d'una funció f definida en els punts x de U i amb valors a R que verifiqui l'equació g(x) = 0, on g és una funció amb valors en un altre espai euclidià.
També s'aplica en equacions diferencials, on és l'eina per demostrar el teorema de redreçament. Una equació diferencial explícita posseeix una forma equivalent a (1) x' = f(t, x). Si la funció f és independent de t l'equació s'anomena autònoma, la funció és un camp vectorial i les solucions de l'equació posseeixen grafiques tangents en un punt x al vector f(x), en la imatge de la figura vermella i groga, a l'esquerra. El teorema del redreçament mostra que localment, l'equació diferencial és equivalent a una que té un camp constant com la de la imatge de la representació blava i groga, també a l'esquerra.
Els exemples esmentats generalment suposen dimensió finita dels espais vectorials considerats. Aquest no és sempre el cas. Una manera d'expressar les solucions de l'equació (1) és de considerar la funció, que a un instant t i a un punt x els associa, el punt imatge de la solució s de (1) que verifica la igualtat s(0) = x. Si la funció f és de classe Cp, llavors aquesta funció α també ho és. Una demostració fa ús del teorema de les funcions implícites en el context d'espais vectorials de dimensió infinita.
Aquests exemples es desenvoluparan a l'article principal.
Demostració[modifica]
Estudi d'un cas[modifica]

Per comprendre el principi de la demostració, s'il·lustra en la funció f de C en C, que a cada z li associa z². L'objectiu és trobar la funció recíproca al veïnatge del punt 1/2(1 + i). Es pot considerar aquesta aplicació com de R² en ell mateix, que a (x, y) li associa (x² - y², 2.x.y). Aquesta aplicació és diferenciable arreu, i en particular al voltant del punt z0 de coordenades (1/2, 1/2). El càlcul de la seva matriu jacobiana Jz dona:
El seva diferencial és inversible en el punt z0 i es nota λ la seva recíproca. L'objectiu és de determinar l'existència d'una aplicació recíproca de f sobre, per exemple, el disc D de centre z0 i de radi 1/5. Aquesta zona s'il·lustra en blau a la figura de dreta i la seva imatge en verd. Per això, cal demostrar que un punt qualsevol z1 de la zona verda, posseeix un únic antecedent per f a la zona blava. En l'exemple s'ha escollit z1 de coordenades (0,1, 0,6), il·lustrat en vermell. Aquesta qüestió és relativament clàssica, un mètode per aconseguir-ho és fer servir el teorema del punt fix. Per això cal que es verifiquin tres hipòtesis: el conjunt considerat ha de ser complet, l'aplicació gy ha de ser d'un conjunt E en ell mateix i ha de ser k-lipschitziana amb k estrictament més petit que 1. L'espai C és complet, no es queda més que a construir la funció adequada g. Se la defineix de D a D per:
En el punt z0, es designa com λ el reciproc del diferencial de f en z0, el diferencial de g és nul. Existeix un veïnatge sobre el qual el diferencial de g és inferior a 1/2, ja que g és contínuament différentiable. El disc D és en aquesta zona. Com que D és a la zona contractant de g, aquest conjunt és estable per g. La imatge del disc D per g correspon a la zona groga, una nova iteració dona una figura simbolitzada per un punt que la petitesa fa gairebé invisible a la figura. Reiterant el procés, s'obté bé un punt fix i el teorema associat indica que aquest punt és únic. Si aquest punt fix es nota ζ, verifica:
Dir que ζ és un punt fix de g equival exactament a dir que és antecedent de z1 per f, el que demostra alhora la seva existència i la seva unicitat.
Existència d'una recíproca local[modifica]
L'enfocament precedent té un avantatge. Enlloc no es fa ús de la dimensió de l'espai vectorial E que conté l'obert U, domini de definició de f. En conseqüència, la demostració és igualment vàlida sobre un espai vectorial normat complet qualsevol, és a dir un espai de Banach. Es fan servir les mateixes notacions d'abans, f és una funció de U en un espai vectorial normat F. Per simplificar l'exposició, es busca demostrar únicament que f és inversible en el punt 0 i se suposa que f(0) = 0. Una vegada s'ha tractat aquest cas, una simple translació permet reduir-lo al cas general.[5] La funció f se suposa de classe Cp amb p estrictament positiu i la diferencial de f en el punt 0 és un isomorfisme continu el recíproc del qual, notat λ, també és continu.[Nota 2] Fixeu-vos que no s'ha suposat que F sigui un espai de Banach, però com que les hipòtesis suposen l'existència d'un isomorfisme bicontinu de E a F, F és necessàriament un espai de Banach.
Sigui φ l'aplicació de U a F, que a x li associa x - λ.f(x).[Nota 3] En 0, l'aplicació posseeix una diferencial nul i, com que aquest diferencial és continu, existeix un real estrictament positiu r tal que la bola oberta Br de centre 0 i de radi r estigui inclosa a U i tal que la norma del diferencial de g sigui sempre estrictament inferior a 1/2 sobre aquesta bola.
L'objectiu és demostrar que f és injectiva sobre la bola de radi ν i centre 0 notada Bν. L'aplicació λ és contínua, sigui m la seva norma, es defineix ν com un real estrictament positiu més petit que r/(2.m). Si y és un punt de Bν, λ.y és de norma estrictament inferior a r/2. Es construeix la funció φy de Br en ella mateixa, on y és un punt de Bν:
L'aplicació φy és amb valors en Br, ja que la norma de λ.y és inferior a r/2, tal com la de φ(x). El teorema del valor mitjà per funcions vectorials mostra que φ és 1/2-lipschitziana i en conseqüència φy també, ja que φy és una translació de φ. El teorema del punt fix mostra l'existència i la unicitat d'un punt fixa de φy sobre Br, el que és equivalent a dir que f és bijectiva de Bν en la seva imatge.
Regularitat de la recíproca[modifica]
Es tracta ara de demostrar que la recíproca de f és de classe Cp. Es nota V la imatge de Bν per f. Siguin y1 i y₂ dos punts qualssevol de V i x1, x₂ els seus antecedents. La continuïtat s'obté observant que φ és 1/2 lipschitziana i:
El que també s'escriu:
Es demostra que el recíproc de f és différentiable sobre V. Sigui y un punt de V i k un vector de F tal que y + k sigui també element de V. Es nota x + h la imatge de y + k pel recíproc de f:
Fixeu-vos que aquí la diferencial se suposa inversible no només en x0 sinó sobre un veïnatge de x0. El conjunt d'isomorfismes inversibles continus formen un obert. Per donar-se'n compte, n'hi ha prou amb fixar-se que si β és un morfisme de norma petita i si α és un isomorfisme bicontinu, α + β s'escriu també α(Id + α-1β) que és el producte de dos isomorfismes bicontinus. Per al segon, n'hi ha prou amb fer servir un desenvolupament en sèrie entera per donar-se'n compte. La sèrie és convergent si la norma de β és estrictament més petita que la del reciproc de α:
Un desenvolupament finit de la funció f mostra que:
On M és un majorant de la norma de la diferencial de f sobre Bν. Tal majorant existeix, ja que φ és contractant sobre Bν i f(x) = λ-1.(x - φ(x)).
Encara falta demostrar que el recíproc de f és de classe Cp. La diferencial del recíproc de f és la composició de la funció f -1 amb la inversa del diferencial de f. La funció inversa és infinitament diferenciable, f és de classe Cp i el recíproc de f és contínua, se'n dedueix que el recíproc de f és de classe C¹. Pas a pas, es verifica que el recíproc de f és de classe Cp.
Vegeu també[modifica]
Referències[modifica]
- ↑ Serge Lang Analyse Réelle InterEditions, Paris 1977 ISBN 2729600590 p 120
- ↑ V&F Bayart Théorèmes d'inversion locale et globale Arxivat 2011-11-05 a Wayback Machine. par le site Bibm@ath.net
- ↑ Es troba un equivalent d'aquest enunciat en: C. Antonini,J-F Quint P Borgnat J Bérard E Lebeau E Souche A Chateau O Teytaud Théorème d'inversion locale Arxivat 2009-11-15 a Wayback Machine. par le site mathématiques.net
- ↑ És el mètode proposat per: Dérivée d'une fonction composée, et d'une fonction réciproque Arxivat 2009-10-09 a Wayback Machine. par le site Homéomath
- ↑ Aquesta convenció és l'escollida per la referència utilitzada per a la demostració S. Lang Analyse Réelle InterEditions, Paris 1977 ISBN 2729600590 p 120
Bibliografia[modifica]
- J'intègre. Cours de mathématiques de 2e année. Ed. Dunod .ISBN 2-10-005412-0
- S. Lang Analyse Réelle InterEditions, Paris 1977 ISBN 2-7296-0059-0
Notes[modifica]
- ↑ Es troba una demostració a l'article derivada de la funció inversa
- ↑ Atenció, en dimensió infinita, un operador no és necessàriament continu i la seva continuïtat no implica la del seu recíproc.
- ↑ S'utilitzen aquí les notacions multiplicatives per a un operador, λ.y significa la imatge de y pel morfisme λ














