Trie

Un trie representant les entrades "as", "pi", "pom", "por" i "poma".

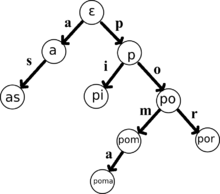
Un trie és un cas especial d'autòmat finit determinista $(S,\Sigma ,T,s,A)$, que serveix per a emmagatzemar un conjunt de cadenes $E$ en el qual:

• $\Sigma$ és l'alfabet sobre el qual estan definides les cadenes;
• $S$, el conjunt d'estats, cadascun dels quals representa un prefix de E;
• la funció de transició: $T:S\times \Sigma \to S$; està definida com segueix: $T(x,\sigma )=x\sigma$ si $x,x\sigma \in S$, i indefinida altrament;
• l'estat inicial $s$ correspon a la cadena buida $\lambda ;$
• el conjunt d'estats d'acceptació $A\subseteq S$ és igual a $E$.

El seu nom procedeix del terme anglés retrieval.

Avantatges

Els avantatges principals dels tries per sobre dels arbres de cerca binària són:

• cerca de claus més ràpida. La cerca d'una clau de longitud $m$ tindrà, en el pitjor dels casos, un cost de l'ordre $O(m)$. Un BST (Binary Search Tree, Arbre de cerca binària en anglés) té un cost de l'ordre $O(logn)$, amb $n$ elements a l'arbre, ja que la cerca depèn de la profunditat de l'arbre, logarítmica amb el nombre de claus
• necessita menys espai per emmagatzemar una gran quantitat de cadenes petites, ja que les claus no s'emmagatzemen explícitament
• té un millor funcionament per a l'algorisme de cerca del prefix més llarg

Aplicacions

Com a substitució d'altres estructures de dades

Substituint taules de dispersió

Un Trie es pot utilitzar per substituir una Taula de dispersió, sobre la qual presenta els següents avantatges:

• el temps de cerca en una taula de dispersió imperfecta és de l'ordre de $O(n)$, i en un trie és de l'ordre de $O(l)$. Açò és degut a les col·lisions de claus
• en un trie no es produeixen col·lisions de claus
• no cal definir cap funció de dispersió, o modificar-la si afegim més claus
• els contenidors que emmagatzemen els distints valors associats a una única clau només són necessaris si tenim més d'un valor associat a una única clau. En una taula de dispersió sempre es necessiten aquestos contenidors per a les col·lisions de clau
• un trie pot proporcionar-nos una ordenació alfabètica de les entrades per clau

Els principals desavantatges dels tries respecte a les taules de dispersió són:

• en determinats casos poden ser més lents que les taules hash en la cerca de dades, especialment si les dades són consultades des de dispositius d'emmagatzematge secundaris, com el disc dur, on el temps d'accés és elevat respecte a la memòria principal
• no és senzill representar totes les claus com a cadenes. Un exemple poden ser els nombres reals, que poden tindre distintes representacions en forma de cadena per a un mateix nombre: p. ex. 1, 1.00, 1.000, +1.000,...
• moltes vegades els tries són més ineficients respecte a l'espai que les taules de dispersió
• els tries no solen estar disponibles amb les eines de desenvolupament de programari, al contrari que les taules de dispersió

Com a representació de diccionaris

Una aplicació freqüent dels tries és l'emmagatzematge de diccionaris, com els que es troben als telèfons mòbils. Aquestes aplicacions s'aprofiten de la capacitat dels tries per fer cerques, insercions i esborrats de manera ràpida. No obstant això, si només es necessita desar paraules (per exemple, no es necessita informació auxiliar de les paraules del diccionari) un autòmat finit determinista acíclic mínim utilitza menys espai que un trie.

Els tries també són útils en la implementació d'algorismes de correspondència aproximada, com els utilitzats al programari de correcció ortogràfica.

Algorismes

El següent pseudocodi determina si una cadena representa un trie.

funció cerca(node, clau) {
si (clau és una cadena buida) { # cas base
retorna (es un node terminal?)
} sinó { # cas recursiu
c = primer_caracter_de_la_clau # això funciona perquè la clau no es buida
cua = clau_mens_el_primer_caràcter
fill = node.fills[c]
si (fill és nul) { # no es pot continuar la cerca del sufix de la clau
retorna fals
} sinó {
retorna cerca(fill,cua)
}
}
}

Nota: fills és un vector amb els fills del node, i un node terminal és aquell que conté una paraula vàlida.

Ordenació

L'ordre lexicogràfic d'un conjunt de claus es pot realitzar com un algorisme simple basat en tries de la següent forma:

• inserir totes les claus en el trie
• obtenir totes les claus mitjançant un recorregut en preordre, per obtenir un ordenament lexicogràfic en ordre ascendent, o mitjançant un recorregut en post-ordre, per obtenir un ordenament lexicogràfic en ordre descendent. El recorregut en preordre i en post-ordre són algorismes de cerca en profunditat d'arbres.

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Trie

Viccionari