Vector normal

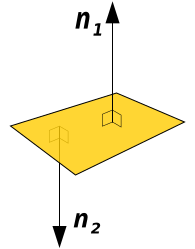En geometria, un vector normal a una entitat geomètrica (línia, corba, superfície, etc.) és un vector d'un espai de producte escalar que conté tant a l'entitat geomètrica com al vector normal, que té la propietat de ser ortogonal a tots els vectors tangents a l'entitat geomètrica.

Un vector normal no necessàriament és un vector normalitzat o unitari.

Exemples

• En $\scriptstyle \mathbb {R} ^{n}$ el vector normal $\scriptstyle \mathbf {n}$ en un punt a una entitat geomètrica té la propietat que per a tot vector del espai tangent de l'entitat en aquest punt satisfà la relació $\scriptstyle \mathbf {n} \cdot \mathbf {t} =0$

Vegeu també

• Ortogonalitat

Referències

Weisstein, Eric W. "Normal Vector." From MathWorld - A Wolfram Web Resource. http://mathworld.wolfram.com/NormalVector.html