Vinclament
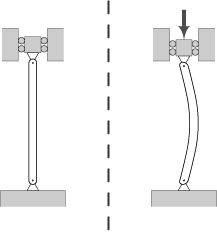
El vinclament és un fenomen d'inestabilitat elàstica que pot donar-se en elements comprimits esvelts, i que es manifesta per l'aparició de desplaçaments importants transversals a la direcció principal de compressió.
Introducció[modifica]
En enginyeria estructural el fenomen apareix principalment en pilars i columnes, i es tradueix en l'aparició d'una flexió addicional en el pilar quan es troba sotmès a l'acció d'esforços axials de certa importància. L'aparició de flexió de vinclament limita severament la resistència a la compressió d'un pilar o qualsevol tipus de peça esvelta. Eventualment, a partir de cert valor de la càrrega axial de compressió, anomenada càrrega crítica de vinclament, pot produir-se una situació d'inestabilitat elàstica i llavors fàcilment la deformació augmentarà produint tensions addicionals que superaran la tensió de ruptura, provocant la ruïna de l'element estructural. A més del vinclament flexional ordinari hi ha el vinclament torsional o inestabilitat elàstica provocat per un moment torsor excessiu.
Hi ha diferents maneres o modes de fallada per vinclament. Per a un element estructural sovint cal verificar diversos d'ells i garantir que les càrregues estan lluny de les càrregues crítiques associades a cada mode o manera de Pando. Els modes típics són:
- Vinclament flexional. Mode de vinclament en el qual un element en compressió es flecta lateralment sense gir ni canvis en la seva secció transversal.
- Vinclament torsional. Mode de vinclament en el qual un element en compressió gira al voltant del seu centre de tall.
- Vinclament flexo-torsional. Mode de vinclament en el qual un element en compressió es flecta i gira simultàniament sense canvis en la seva secció transversal.
- Vinclament lateral-torsional. Mode de vinclament d'un element a flexió que involucra deflexió normal al pla de flexió i, de manera simultània, gir al voltant del centre de tall
Vinclament flexional[modifica]
Els pilars i les barres comprimides de gelosies poden presentar diverses maneres d'error en funció de la seva esveltesa mecànica:
- Els pilars molt esvelts solen fallar per vinclament elàstic i són sensibles tant al vinclament local el mateix pilar com al vinclament global de l'estructura completa.
- En els pilars d'esveltesa mitjana les imperfeccions constructives com les heterogeneïtats són particularment importants es poden presentar vinclament anelástico.
- Els pilars de molt baixa esveltesa fallen per excés de compressió, abans que els efectes del vinclament resultin importants.
Vinclament local[modifica]

El vinclament local és el que apareix en peces o elements aïllats o que estructuralment poden considerar aïllats. En aquest cas la magnitud de la càrrega crítica ve donada segons el cas per la fórmula de Leonhard Euler o la Engesser. La càrrega crítica d'Euler depèn de la longitud de la peça, del material, de la seva secció transversal i de les condicions d'unió, vinculació o subjecció en els extrems. Per a una peça que pot considerar-biarticulada en els seus extrems, la càrrega crítica d'Euler és:
(1)
Sent: P crit , la càrrega crítica; L , Mòdul de Young del material de què està feta la barra; I min , moment d'inèrcia mínim de la secció transversal de la barra; L , longitud de la barra i λ l'esveltesa mecànica de la peça.
Quan les condicions de subjecció dels extrems són diferents la càrrega crítica d'Euler ve donada per una equació del tipus:
(2)
Al producte s'anomena longitud de vinclament .
Vinclament global[modifica]
En una estructura complexa formada per barres i altres elements enllaçats poden aparèixer maneres de deformació en els quals els desplaçaments no siguin proporcionals a les càrregues i l'estructura pot panda globalment sense que cap de les barres o elements estructurals abast la seva pròpia càrrega de vinclament. A causa d'aquest factor, la càrrega crítica global de cert tipus d'estructures (per exemple en entramats de cúpules monocapa) és molt menor que la càrrega crítica (local) de cadascun dels seus elements.
El tipus d'estructura més simple que presenta vinclament global per càrrega crítica diferent de la dels seus elements està format per dues barres articulades entre si[1] ia la fonamentació, que es mostra a la figura.
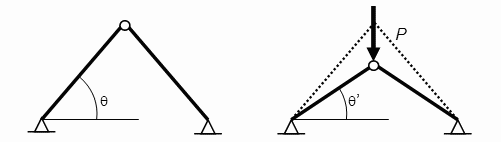
Les equacions que governen el comportament de l'estructura són:
- Relació elàstica entre escurçament i esforç axial:
- Relació geomètrica de les configuracions no-deformada i deformada:
On: N , esforç axial de cadascuna de les barres; Δ L , escurçament patit per les barres per adoptar la configuració deformada; Δθ = θ-θ ', és la diferència de ángulos mostrada a la figura; L , mòdul de Young del material de les barres; A , àrea transversal de cadascuna de les barres; L , longitud inicial de cada una de les dues barres.
Substituint la segona de les equacions en la primera, aclarint Δ L de la tercera i substituint el seu valor també el seu valor a la primera s'arriba a:
El valor de Δθ per al qual s'assoleix el màxim és precisament la càrrega crítica global. Les càrregues de vinclament global i local venen donades per:
Cadascuna aquestes càrregues presenta maneres d'error diferents en l'estructura. D'entre els dos possibles modes de fallada per vinclament passarà el que presenti un angle d'aparició major on aquests ángulos venen donats per:
Pla de vinclament[modifica]
El pla de vinclament es refereix al pla que contindrà l'inici de la deformada d'una peça sotmesa a compressió dominant. El pla de vinclament conté l'eix baricentre de la biga i sobre ell la deflexió per vinclament és màxima. Per a una peça sotmesa només a compressió sense moments apreciables addicionals, el pla de vinclament coincidirà amb el pla perpendicular sigui paral·lela a l'eix de menys inèrcia de la secció.
Vinclament torsional[modifica]
En bigues d'ales amples o d'escassa rigidesa torsional, el vinclament flexional convencional pot anar acompanyat de l'aparició d'una torsió de la secció, resultant una manera d'error mixt conegut com a vinclament torsional o vinclament lateral. El moment torsor crític per al qual apareixeria aquest tipus d'error ve donat per:[2]
On les noves magnituds són:
- , és el moment d'inèrcia a mínim en flexió.
- , són, respectivament, el mòdul de alabeig i el mòdul de torsió.
- , el mòdul d'elasticitat transversal.
I la resta de magnituds tenen el mateix significat que per al vinclament flexional pur. En peces on el moment de alabeig és menyspreable es pot utilitzar l'expressió aproximada:
Càlcul de càrregues crítiques[modifica]
Corba elàstica[modifica]
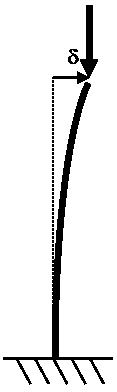
Una manera de trobar la càrrega crítica d'una estructura consisteix a pressuposar la forma qualitativa en què aquesta panda, parametritzat aquesta forma qualitativa mitjançant diversos paràmetres incògnita. Introduint aquesta forma qualitativa en l'equació de la corba elàstica i buscant que la solució parametritzada satisfaci les condicions de contorn qualitatives, que normalment es refereixen a desplaçaments i girs dels nusos de les barres de l'estructura, s'obtenen relacions entre els paràmetres incògnita introduïts. El valor de la càrrega crítica és precisament allò que fa que aquestes relacions es compleixin.
El mètode d'Euler per barres aïllades és un exemple d'ús d'aquest mètode. Per exemple per determinar la càrrega de crítica d'un pilar encastat a la base i lliure a l'extrem tractem de resoldre l'equació de la corba elàstica sota les següents condicions:
La solució d'aquesta equació, en funció del paràmetre de desplaçament horitzontal del pilar, resulta ser:
La condició de contorn a l'extrem superior (on h = H i w sup = δ) només es compleix per a certs valors de P , que compleixen:
El menor d'aquests valors és precisament el valor acceptat per a la càrrega crítica d'Euler d'un pilar encastat a la base i lliure a la part superior:
Mètodes energètics[modifica]
Per a estructures d'una certa complexitat el mètode anterior resulta de molt difícil aplicació, ja que requereix integrar un nombre elevat d'equacions diferencials per a cada element lineal de l'estructura.
Un mètode aproximat consisteix a pressuposar aproximadament les deformacions associades al vinclament, que satisfaci les condicions de contorn en els extrems de les peces, i en igualar l'energia de deformació W int amb el treball exterior realitzat per la força que produeix el fenomen de vinclament W ext durant la deformació, W int = W ext . Aquestes dues equacions es poden escriure en termes el camp de desplaçaments dels moments flectors associats. Per a cada element lineal l'energia de deformació i el treball exterior venen donats per:
Com més ajustat sigui el camp de desplaçaments suposat w ( x ) millors resultats dona el mètode anterior.
Dimensionament d'elements sotmesos a vinclament[modifica]
En enginyeria estructural hi ha una necessitat pràctica de dimensionar els elements lineals sotmesos a compressió amb la suficient secció transversal perquè no fallin per vinclament. La secció transversal necessària perquè això no passi és moltes vegades més gran que la que seria necessària per a suportar un esforç de tracció de la mateixa magnitud (entre 1,5 i 6 vegades a la majoria de casos). La majoria de normes usen un coeficient de reducció de la resistència quan l'esforç sobre l'element lineal és de compressió i no de tracció. El Eurocodi per exemple dona per a la resistència d'un pilar sotmès a compressió i tracció simples les següents resistències:
On:
- són respectivament el esforç axial últim en tracció i l'esforç axial últim en compressió.
- són l'àrea bruta de la secció transversal i l'àrea efectiva de la secció transversal (per a la majoria de seccions transversals, totes dues coincideixen).
- , és la tensió màxima admissible sobre el material.
- , és el coeficient khi de reducció de la resistència per vinclament.
El mateix coeficient es pot usar per estimar per excés la tensió i determinar si un element és segur. Així quan un element està sotmès a flexió o compressió compostes la tensió de referència per a calcular si l'element és segur o no es pren aproximadament com:
On:
- és l'esforç axial a què està sotmès l'element.
- , són els moments flectors mesurats segons les dues direccions principals d'inèrcia.
- , són els moments resistents associats als moments principals d'inèrcia de la secció transversal.
En situacions on les tensions tangents i el alabeig seccional de la secció siguin importants s'ha de substituir el membre abans del signe de menys que, per la tensió de Von Mises i en l'expressió de Navier ha de comptabilitzar l'efecte del bimoment.
Referències[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Vinclament |
- ↑ «Estabilitat de cúpules en Tecnun ». Arxivat de l'original el 2008-09-20. [Consulta: 17 febrer 2010].
- ↑ 20CD-ROM/metchp4.pdf Load Tables for flexural Members and Connections[Enllaç no actiu]
Vegeu també[modifica]
- Esveltesa mecànica
- Prisma mecànic, resistència de materials
- Més sobre Vinclament a la Gestió de
- Vinclament per abonyegadura en làmines
















![{\displaystyle w(h)=\delta \left[1-\cos \left(h{\sqrt {\frac {P}{EI}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a10d7a4860f258a79e1d27eb030abcfc797ed6ba)


![{\displaystyle W_{int}={\frac {1}{2}}\int _{0}^{L}EI\left[{\frac {d^{2}w(x)}{dx^{2}}}\right]^{2}dx\qquad \qquad W_{ext}={\frac {P_{crit}}{2}}\int _{0}^{L}\left[{\frac {dw(x)}{dx}}\right]^{2}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bbb19e7a704558d2a1cfc93995e6b28e8dd03b5)








