Baricentre: diferència entre les revisions
Pàgina nova, amb el contingut: «La definició més usual és: en un triangle punt que es troba a la intersecció de les línies que uneixen els vèrtex i la mitjana del costat oposat. Agafant ...». |
orto |
||
| Línia 1: | Línia 1: | ||
El '''baricentre''' d'un [[triangle]] és el punt que es troba a la intersecció de les línies que uneixen els [[vèrtexs]] i la mitjana del costat oposat. Agafant una d'aquestes línies, el baricentre es troba a 2/3 de distància del vèrtex i 1/3 del costat oposat. |
|||
Això, però no és ni molt menys general ni acurat. |
Això, però, no és ni molt menys general ni acurat. L'explicació més científica i general és: |
||
Siguin A<sub>1</sub>, ... A<sub>n</sub> ''n'' punts, i m<sub>1</sub>, ... m<sub>n</sub> ''n'' números (''m'' com ''massa'' ). |
Siguin A<sub>1</sub>, ... A<sub>n</sub> ''n'' punts, i m<sub>1</sub>, ... m<sub>n</sub> ''n'' números (''m'' com ''massa'' ). |
||
Llavors el baricentre dels ( A<sub>i</sub>, m<sub>i</sub> ) és el punt G definit de la següent manera: |
Llavors el baricentre dels ( A<sub>i</sub>, m<sub>i</sub> ) és el punt G definit de la següent manera: |
||
| Línia 7: | Línia 7: | ||
:<math>\overrightarrow{OG\,} = \frac{\sum{m_i\overrightarrow{O\!A_i}}}{\sum{m_i}} = \frac{m_1\overrightarrow{O\!A_1} + ...+m_n\overrightarrow{O\!A_n}} {m_1+...+m_n}, \quad \mbox{con} \quad \sum{m_i} \ne 0</math> |
:<math>\overrightarrow{OG\,} = \frac{\sum{m_i\overrightarrow{O\!A_i}}}{\sum{m_i}} = \frac{m_1\overrightarrow{O\!A_1} + ...+m_n\overrightarrow{O\!A_n}} {m_1+...+m_n}, \quad \mbox{con} \quad \sum{m_i} \ne 0</math> |
||
Aquesta definició no depèn del punt O, que pot ser qualsevol. Si s'agafa l'origen del pla o de l'espai, s'obtenen les coordenades del baricentre, com a |
Aquesta definició no depèn del punt O, que pot ser qualsevol. Si s'agafa l'origen del pla o de l'espai, s'obtenen les coordenades del baricentre, com a mitjana ponderada pels mi, de les coordenades dels punts Ai: |
||
:<math>x_G=\frac{\sum{m_ix_i}}{\sum{m_i}}=\frac{m_1x_1+...+m_nx_n} |
:<math>x_G=\frac{\sum{m_ix_i}}{\sum{m_i}}=\frac{m_1x_1+...+m_nx_n} |
||
| Línia 14: | Línia 14: | ||
La definició anterior equival a la fórmula següent, més pràctica pel càlcul vectorial, ja que prescindeix de les fraccions (s'obté agafant O=G): |
La definició anterior equival a la fórmula següent, més pràctica pel càlcul vectorial, ja que prescindeix de les fraccions (s'obté agafant O=G): |
||
:<math>\sum_{i=1}^n{m_i\overrightarrow{G\!A_i}} = \vec 0 \quad \mbox{o |
:<math>\sum_{i=1}^n{m_i\overrightarrow{G\!A_i}} = \vec 0 \quad \mbox{o bé} \quad m_1\overrightarrow{G\!A_1} + ...+m_n\overrightarrow{G\!A_n} = \vec 0</math> |
||
Un '''isobaricentre''' (''iso'': mateix) és un baricentre amb totes les masses iguals entre si; és usual en aquest cas prendre-les iguals a 1. Si no es precisen les masses, el baricentre és per defecte l'isobaricentre. |
Un '''isobaricentre''' (''iso'': mateix) és un baricentre amb totes les masses iguals entre si; és usual en aquest cas prendre-les iguals a 1. Si no es precisen les masses, el baricentre és per defecte l'isobaricentre. |
||
El baricentre coincideix amb la noció física de [[centre de massa]], exemples: |
El baricentre coincideix amb la noció física de [[centre de massa]], exemples: |
||
*El baricentre d'{A, B} és el centre de massa del segment [A;B], o sigui d'una barra d' |
*El baricentre d'{A, B} és el centre de massa del segment [A;B], o sigui d'una barra d'extrems A i B, de massa uniformement distribuïda. |
||
*El baricentre d'{A, B, C} és el centre de gravetat del triangle ABC, suposant-li una densitat superficial uniforme (per exemple si tallem un triangle de cartró. |
*El baricentre d'{A, B, C} és el centre de gravetat del triangle ABC, suposant-li una densitat superficial uniforme (per exemple si tallem un triangle de cartró. Correspon al punt on es tallen les mitjanes. El triangle es mantindrà en equilibri (inestable) a la punta d'un llapis o d'un compàs, si aquest està situat just sota del centre de massa. El baricentre d'un [[triangle]] té, a més la propietat de pertànyer a la [[recta d'Euler]]. |
||
*El baricentre de quatre punts {A, B, C, D} de l'espai és el centre de gravetat del [[tetraedre]], suposant-li una densitat volúmica uniforme. Correspòn al punt on es tallen els segments que uneixen cada vèrtex amb l'isobaricentre de la cara oposada. |
*El baricentre de quatre punts {A, B, C, D} de l'espai és el centre de gravetat del [[tetraedre]], suposant-li una densitat volúmica uniforme. Correspòn al punt on es tallen els segments que uneixen cada vèrtex amb l'isobaricentre de la cara oposada. |
||
Es pot generalitzar l'anterior en qualsevol situació. |
Es pot generalitzar l'anterior en qualsevol situació. |
||
| Línia 26: | Línia 26: | ||
[[Imatge:baricentros.png]] |
[[Imatge:baricentros.png]] |
||
La |
La coincidència del baricentre i el centre de gravetat permet localitzar el primer d'una forma senzilla. Si agafem el tros de cartró abans comentat i l'aguantem verticalment des de qualsevol dels seus punts, girarà fins que el centre de gravetat (baricentre) es situï justament en la vertical del punt de subjecció; marcant aquesta vertical sobre el cartró i repetint el procés aguantant des d'un segon punt, trobarem el baricentre en el punt d'intersecció. |
||
'''Propietats [[topologia|topològiques]]:''' |
'''Propietats [[topologia|topològiques]]:''' |
||
El baricentre G d'(A, a) i (B, b) amb a i b |
El baricentre G d'(A, a) i (B, b) amb a i b qualssevol, està unicada en la recta (AB). Si a i b son ambdós positius, G pertany al segment [A,B]. En aquest cas els coeficients a i b es poden llegir en el gràfic. Per exemple: |
||
:<math>\overrightarrow{AG\,} = {5 \over 7}\, \overrightarrow{GB\,} \quad \Leftrightarrow \quad 7\, \overrightarrow{AG\,} = 5\, \overrightarrow{GB\,} \quad \Leftrightarrow \quad 7\, \overrightarrow{GA\,} + 5\, \overrightarrow{GB\,} = \vec 0</math> |
:<math>\overrightarrow{AG\,} = {5 \over 7}\, \overrightarrow{GB\,} \quad \Leftrightarrow \quad 7\, \overrightarrow{AG\,} = 5\, \overrightarrow{GB\,} \quad \Leftrightarrow \quad 7\, \overrightarrow{GA\,} + 5\, \overrightarrow{GB\,} = \vec 0</math> |
||
| Línia 36: | Línia 36: | ||
I per tant G = bar { (A, 7), (B, 5) }. És suficient doncs permutar les longituds del gràfic per obtenir les masses dels punts. |
I per tant G = bar { (A, 7), (B, 5) }. És suficient doncs permutar les longituds del gràfic per obtenir les masses dels punts. |
||
El baricentre G de tres |
El baricentre G de tres punts de l'espai (A, a), (B, b) i (C, c) amb a i b qualssevol està ubicat en el pla (ABC). Si són tots positius, G pertany al triangle ABC. |
||
Per suposat aquestes propietats es generalitzen en totes les dimensions. |
Per suposat aquestes propietats es generalitzen en totes les dimensions. |
||
'''Propietats [[àlgebra|algebraiques]]:''' |
'''Propietats [[àlgebra|algebraiques]]:''' |
||
* ''' |
* '''Homogeneïtat''': no canvia el baricentre si es multiplica totes les masses per un mateix factor k ≠ 0. |
||
formalment: bar { (A<sub>1</sub>, m<sub>1</sub>), ... , (A<sub>n</sub>, m<sub>n</sub>) } = bar { (A<sub>1</sub>, km<sub>1</sub>), ... , (A<sub>n</sub>, km<sub>n</sub>) }. |
formalment: bar { (A<sub>1</sub>, m<sub>1</sub>), ... , (A<sub>n</sub>, m<sub>n</sub>) } = bar { (A<sub>1</sub>, km<sub>1</sub>), ... , (A<sub>n</sub>, km<sub>n</sub>) }. |
||
| Línia 47: | Línia 47: | ||
Per exemple, si D = bar {(A, a), (B, b)} (amb a + b ≠ 0) llavors bar {(A, a), (B, b), (C, c)} = bar {(D,'''a + b'''), (C, c)} (a + b + c ≠ 0) |
Per exemple, si D = bar {(A, a), (B, b)} (amb a + b ≠ 0) llavors bar {(A, a), (B, b), (C, c)} = bar {(D,'''a + b'''), (C, c)} (a + b + c ≠ 0) |
||
Exemple de demostració: Considerem de nou el centre de massa d'un triangle ABC. anomenem I el centre del segment [B,C]. |
Exemple de demostració: Considerem de nou el centre de massa d'un triangle ABC. anomenem I el centre del segment [B,C]. Llavors I = bar { (B, 1), (C, 1)}. Després G = bar {(A, 1), (B, 1), (C, 1)} = bar {(A, 1), (I, 2)}, el que significa que G està al segment [A,I], a un terç del camí a partir d'I. |
||
El baricentre es pot definir en matemàtiques amb coeficients negatius. Com que no existeixen masses negatives, qui significat físic es pot atribuir a aquests càlculs?. Heus aquí un exemple molt senzill: en un full de cartró, retallem una mitja lluna com mostra la figura següent, |
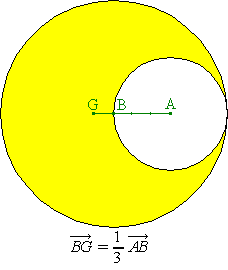
El baricentre es pot definir en matemàtiques amb coeficients negatius. Com que no existeixen masses negatives, qui significat físic es pot atribuir a aquests càlculs?. Heus aquí un exemple molt senzill: en un full de cartró, retallem una mitja lluna com mostra la figura següent, constituït d'un cercle en el qual hem tret un altre cercle de radi dos cops menor. Ens pregutem quin és el centre de massa del creixent. |
||
El càlcul resulta molt simplificat si considerem la mitja lluna com una juxtaposició de dos discs, un gran amb massa positiva, i l'altre, petit, amb massa negativa. Les masses són proporcionals a les àrees (densitat uniforme), el que dóna una massa de 4 pel primer disc, i de -1 pel segon. Llavors G = bar {(A, -1), (B, 4)}. |
El càlcul resulta molt simplificat si considerem la mitja lluna com una juxtaposició de dos discs, un gran amb massa positiva, i l'altre, petit, amb massa negativa. Les masses són proporcionals a les àrees (densitat uniforme), el que dóna una massa de 4 pel primer disc, i de -1 pel segon. Llavors G = bar {(A, -1), (B, 4)}. |
||
| Línia 55: | Línia 55: | ||
[[Imatge:baricentro_luna.png]] |
[[Imatge:baricentro_luna.png]] |
||
''' |
'''Càlcul geomètric del baricentre:''' |
||
El càlcul geomètric (amb regle i compàs) del baricentre d'una manera ràpida d'un [[polígon]] (regular o irregular), es pot realitzar així: |
El càlcul geomètric (amb regle i compàs) del baricentre d'una manera ràpida d'un [[polígon]] (regular o irregular), es pot realitzar així: |
||
Si tenim un polígon d' |
Si tenim un polígon d'un vèrtex: |
||
* Descomposam el polígon en triangles i quadrilàters disjunts (que no tinguin vèrtex en comú) |
|||
* |
* Calculam els baricentres d'aquests triangles i quadrilàters, i formar el polígon corresponent. |
||
| ⚫ | |||
* Calcular els baricentres d'aquests triangles i quadrilàters, i formar el polígon corresponent. |
|||
| ⚫ | |||
Es pot demostrar que aquest [[algoritme]] té ordre logarítmic. |
Es pot demostrar que aquest [[algoritme]] té ordre logarítmic. |
||
[[Categoria:Geometria]] |
[[Categoria:Geometria]] |
||
[[Categoria:Mecànica]] |
[[Categoria:Mecànica]] |
||
[[cs:Těžiště]] |
[[cs:Těžiště]] |
||
Revisió del 14:33, 28 juny 2007
El baricentre d'un triangle és el punt que es troba a la intersecció de les línies que uneixen els vèrtexs i la mitjana del costat oposat. Agafant una d'aquestes línies, el baricentre es troba a 2/3 de distància del vèrtex i 1/3 del costat oposat.
Això, però, no és ni molt menys general ni acurat. L'explicació més científica i general és: Siguin A1, ... An n punts, i m1, ... mn n números (m com massa ). Llavors el baricentre dels ( Ai, mi ) és el punt G definit de la següent manera:
Aquesta definició no depèn del punt O, que pot ser qualsevol. Si s'agafa l'origen del pla o de l'espai, s'obtenen les coordenades del baricentre, com a mitjana ponderada pels mi, de les coordenades dels punts Ai:
La definició anterior equival a la fórmula següent, més pràctica pel càlcul vectorial, ja que prescindeix de les fraccions (s'obté agafant O=G):
Un isobaricentre (iso: mateix) és un baricentre amb totes les masses iguals entre si; és usual en aquest cas prendre-les iguals a 1. Si no es precisen les masses, el baricentre és per defecte l'isobaricentre.
El baricentre coincideix amb la noció física de centre de massa, exemples:
- El baricentre d'{A, B} és el centre de massa del segment [A;B], o sigui d'una barra d'extrems A i B, de massa uniformement distribuïda.
- El baricentre d'{A, B, C} és el centre de gravetat del triangle ABC, suposant-li una densitat superficial uniforme (per exemple si tallem un triangle de cartró. Correspon al punt on es tallen les mitjanes. El triangle es mantindrà en equilibri (inestable) a la punta d'un llapis o d'un compàs, si aquest està situat just sota del centre de massa. El baricentre d'un triangle té, a més la propietat de pertànyer a la recta d'Euler.
- El baricentre de quatre punts {A, B, C, D} de l'espai és el centre de gravetat del tetraedre, suposant-li una densitat volúmica uniforme. Correspòn al punt on es tallen els segments que uneixen cada vèrtex amb l'isobaricentre de la cara oposada.
Es pot generalitzar l'anterior en qualsevol situació.
La coincidència del baricentre i el centre de gravetat permet localitzar el primer d'una forma senzilla. Si agafem el tros de cartró abans comentat i l'aguantem verticalment des de qualsevol dels seus punts, girarà fins que el centre de gravetat (baricentre) es situï justament en la vertical del punt de subjecció; marcant aquesta vertical sobre el cartró i repetint el procés aguantant des d'un segon punt, trobarem el baricentre en el punt d'intersecció.
Propietats topològiques:
El baricentre G d'(A, a) i (B, b) amb a i b qualssevol, està unicada en la recta (AB). Si a i b son ambdós positius, G pertany al segment [A,B]. En aquest cas els coeficients a i b es poden llegir en el gràfic. Per exemple:
I per tant G = bar { (A, 7), (B, 5) }. És suficient doncs permutar les longituds del gràfic per obtenir les masses dels punts.
El baricentre G de tres punts de l'espai (A, a), (B, b) i (C, c) amb a i b qualssevol està ubicat en el pla (ABC). Si són tots positius, G pertany al triangle ABC. Per suposat aquestes propietats es generalitzen en totes les dimensions.
Propietats algebraiques:
- Homogeneïtat: no canvia el baricentre si es multiplica totes les masses per un mateix factor k ≠ 0.
formalment: bar { (A1, m1), ... , (An, mn) } = bar { (A1, km1), ... , (An, kmn) }.
- Associativitat: el baricentre es pot calcular reagrupant punts, és a dir, introduint baricentres parcials.
Per exemple, si D = bar {(A, a), (B, b)} (amb a + b ≠ 0) llavors bar {(A, a), (B, b), (C, c)} = bar {(D,a + b), (C, c)} (a + b + c ≠ 0)
Exemple de demostració: Considerem de nou el centre de massa d'un triangle ABC. anomenem I el centre del segment [B,C]. Llavors I = bar { (B, 1), (C, 1)}. Després G = bar {(A, 1), (B, 1), (C, 1)} = bar {(A, 1), (I, 2)}, el que significa que G està al segment [A,I], a un terç del camí a partir d'I.
El baricentre es pot definir en matemàtiques amb coeficients negatius. Com que no existeixen masses negatives, qui significat físic es pot atribuir a aquests càlculs?. Heus aquí un exemple molt senzill: en un full de cartró, retallem una mitja lluna com mostra la figura següent, constituït d'un cercle en el qual hem tret un altre cercle de radi dos cops menor. Ens pregutem quin és el centre de massa del creixent.
El càlcul resulta molt simplificat si considerem la mitja lluna com una juxtaposició de dos discs, un gran amb massa positiva, i l'altre, petit, amb massa negativa. Les masses són proporcionals a les àrees (densitat uniforme), el que dóna una massa de 4 pel primer disc, i de -1 pel segon. Llavors G = bar {(A, -1), (B, 4)}.
Càlcul geomètric del baricentre:
El càlcul geomètric (amb regle i compàs) del baricentre d'una manera ràpida d'un polígon (regular o irregular), es pot realitzar així:
Si tenim un polígon d'un vèrtex:
- Descomposam el polígon en triangles i quadrilàters disjunts (que no tinguin vèrtex en comú)
- Calculam els baricentres d'aquests triangles i quadrilàters, i formar el polígon corresponent.
- Tornam al primer pas
Es pot demostrar que aquest algoritme té ordre logarítmic.