Corba de Peano

Giuseppe Peano

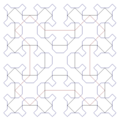
Una corba de Peano és una corba plana parametritzada per una funció contínua de l'interval unitat [0, 1], exhaustiva cap al quadrat [0, 1]×[0, 1], és-a-dir que la corba passa per cada punt del quadrat: « omple l'espai ». Totes aquestes corbes són fractals: encara que estan formades per una línia són de dimensió 2. Aquest tipus de corbes s'anomenen així en l'honor de Giuseppe Peano, que va ser el primer a descriure'n una.

Història

En un article de 1890 Giuseppe Peano descriu una corba auto-intersectant que passa per tots els punts de la superfície del quadrat unitat. El seu objectiu és construir una aplicació des de l'interval unitat definit sobre $\scriptstyle {\mathbb {R} }$ vers el quadrat unitat definit sobre $\scriptstyle {\mathbb {R} ^{2}}$ . Il·lustra així un resultat de Georg Cantor del 1877 que estableix que el conjunt dels punts de l'interval unitat i el d'una superfície bidimensioal finita tenen el mateix cardinal. Peano aporta la prova de que una funció d'aquet tipus pot ser contínua. És a dir que una corba pot omplir una superfície.

La clau passa per l'elaboració d'una corba que no és derivable enlloc. Totes les corbes trobades fins llavors eren derivables per intervals (tenien una derivada contínua sobre cada interval). El 1872, Karl Weierstrass havia descrit una funció que era contínua en tots els punts però no era derivable en cap punt. Però cap d'aquestes corbes no podia omplir el quadrat unitat. La corba de Peano, és al'hora no derivable enlloc i omple el pla, era doncs fortament contra-intuïtiva.

Peano utilitza l'existència d'una notació en base tres per a tot nombre real. En el conjunt de les sucessions de valors de {0,1,2}, construeix una correspondència entre la sucessió: $T=(a_{n})_{n\in \mathbb {N} ^{*}}$ i la parella de sucessions $(X,Y)=((b_{n})_{n\in \mathbb {N} ^{*}},(c_{n})_{n\in \mathbb {N} ^{*}})$ de la següent manera:

• $b_{n}=a_{2n-1}{\text{ ou }}2-a_{2n-1}$ segons si la suma dels termes de rang parell de la successió $(a_{n})$ : $\sum _{1\leq k\leq n-1}a_{2k}$ : és parella o senar (per convenció, la suma buida $\sum _{1\leq k\leq 0}a_{2k}$ és nul·la i per tant parella, doncs $b_{1}=a_{1}$)
• $c_{n}=a_{2n}{\text{ ou }}2-a_{2n}$ segons si la suma dels termes de rang senar de la successió $(a_{n})$ : $\sum _{k=1}^{n}a_{2k-1}$ és parella o senar.

Quatre iteracions de la corba de Peano

A cada successió, li associa el real del qual la successió n'és un desenvolupament en base 3

$t=0,a_{1}a_{2}\cdots a_{n}\cdots =\sum _{k=1}^{+\infty }a_{k}3^{-k},\qquad x=0,b_{1}b_{2}\cdots b_{n}\cdots =\sum _{k=1}^{+\infty }b_{k}3^{-k},\qquad y=0,c_{1}c_{2}\cdots c_{n}\cdots =\sum _{k=1}^{+\infty }c_{k}3^{-k}$

i demostra que la correspondència que, al real t, li associa la parella de reals (x,y) és una aplicació exhaustiva i contínua de [0,1] en [0,1]×[0,1].

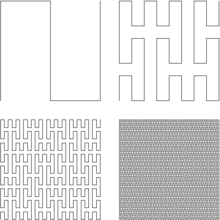
L'article de Peano no contenia pas cap il·lustració. Una observació de les successions T, nul·les a partir del rang 3, conduiria a la construcció successiva dels punts de coordenades (0,0), (0,1/3), (0,2/3), (1/3,2/3), (1/3,1/3), (1/3,0), (2/3,0), (2/3,1/3), (2/3,2/3) que, units per segments rectes donen una corba analoga a l'etapa 1 de la il·lustració de dalt. Per les successions nul·les a partir del rang cinc, es traça una corba analoga a la iteració 2 de dalt, començant al punt de coordenades (0,0) i acabant al punt de coordenades (8/9,8/9).

Un any més tard, David Hilbert publica una construcció nova i més simple, coneguda avui amb el nom de corba de Hilbert. El seu article de 1891 és el primer a proposar una illustration de la seva construcció.

La majoria de les corbes de Peano es construeixen seguint un procediment iteratiu i són el límit d'una successió de corbes poligonals.

A partir dels l'exemples de Peano i de Hilbert, s'han dissenyat altres corbes contínues, obertes o tancades :

• el 1900, el matemàtic Eliakim Hastings Moore proposa, quatre corbes de Hilbert, una variant tancada s'anomena avui corba de Moore;
• el 1905, Henri Lebesgue proposa una nova corba que és derivable gairebé a tots els punts;
• en 1912, el matemàtic polones Wacław Sierpińesquí per la seva banda va descriure una altra corba tancada que actualment porta el seu nom.

Més tard Walter Wunderlich desenvolupa, una família sencera de variantes de la corba original de Peano.

• 
  Corba de Hilbert
• 
  Corba de Sierpinski (en)
• 
  Corba de Moore (en)
• 
  Corba de Lebesgue

Propietats

• Contràriament les aproximacions successives que tendeixen a elles, les quals en general són corbes que no se solapen pas, una corba de Peano és auto-intersectant i correspon a una funció no injectiva.
• La corba de Peano és 1/2-hölderiana. Tanmateix, és impossible d'obtenir una aplicació a-hölderiana exhaustiva de [0,1] a [0,1]2 per a>1/2