Topologia quocient: diferència entre les revisions
Contingut suprimit Contingut afegit
m Robot treu puntuació penjada després de referències |
m robot estandarditzant mida de les imatges, localitzant i simplificant codi |
||
| Línia 1: | Línia 1: | ||
[[Fitxer:Banda_Möbius.png| |
[[Fitxer:Banda_Möbius.png|miniatura|La [[cinta de Möbius]] es pot veure com un espai topològic quocient (veure el segon exemple).]] |
||
En [[matemàtiques]], la '''topologia quocient''' és una topologia definida sobre el [[conjunt quocient]] generat per una [[relació d'equivalència]] sobre un [[espai topològic]]. |
En [[matemàtiques]], la '''topologia quocient''' és una topologia definida sobre el [[conjunt quocient]] generat per una [[relació d'equivalència]] sobre un [[espai topològic]]. |
||
| Línia 15: | Línia 15: | ||
== Exemples == |
== Exemples == |
||
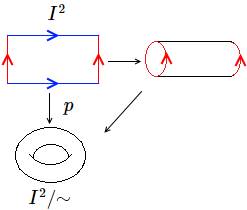
*El [[Tor (geometria)|tor]] com a conjunt quocient:<ref name="mtf"></ref> Sobre <math>I^2 = [0,1]\times [0,1]</math> es defineix la relació d'equivalència <math>(x,0)\mathcal{R} (x,1)</math> i <math>(0,y)\mathcal{R} (1,y)</math>. L'espai quocient <math>I^2 /\mathcal{R}</math> és [[homeomorfisme|homeomorf]] a un tor. |
*El [[Tor (geometria)|tor]] com a conjunt quocient:<ref name="mtf"></ref> Sobre <math>I^2 = [0,1]\times [0,1]</math> es defineix la relació d'equivalència <math>(x,0)\mathcal{R} (x,1)</math> i <math>(0,y)\mathcal{R} (1,y)</math>. L'espai quocient <math>I^2 /\mathcal{R}</math> és [[homeomorfisme|homeomorf]] a un tor. |
||
:[[ |
:[[Fitxer:Construccion Toro.png|center|Tor]] |
||
*La [[cinta de Möbius]] com a conjunt quocient:<ref name="mtf"></ref> Sobre <math>I^2</math> es defineix la relació d'equivalència <math>(0,y)\mathcal{R} (1,1-y)</math>. L'espai quocient <math>I^2 /\mathcal{R}</math> és homeomorf a una cinta de Möbius. |
*La [[cinta de Möbius]] com a conjunt quocient:<ref name="mtf"></ref> Sobre <math>I^2</math> es defineix la relació d'equivalència <math>(0,y)\mathcal{R} (1,1-y)</math>. L'espai quocient <math>I^2 /\mathcal{R}</math> és homeomorf a una cinta de Möbius. |
||
:[[ |
:[[Fitxer:Möbius2.png|center|Banda de Möbius]] |
||
*La [[ampolla de Klein]] com a conjunt quocient:<ref>{{ref-publicació |cognom=A. Stolz |nom=Stephan |article=Topología algebraica |url=https://www3.nd.edu/~stolz/2016S_Math60440/Alg_Top_2016.pdf |consulta= 18 de setembre de 2019 |llengua=anglès|publicació=[[Universitat de Notre Dame]]}}</ref> Sobre <math>I^2</math> es defineix la relació d'equivalència <math>(x,0)\mathcal{R} (x,1)</math> i <math>(0,y)\mathcal{R} (1,1-y)</math>. L'espai quocient <math>I^2 /\mathcal{R}</math> és homeomorf a una ampolla de Klein (es difícil de visualitzar ja que no és homeomorf a un subespai de <math>\mathbb{R}^3</math>). |
*La [[ampolla de Klein]] com a conjunt quocient:<ref>{{ref-publicació |cognom=A. Stolz |nom=Stephan |article=Topología algebraica |url=https://www3.nd.edu/~stolz/2016S_Math60440/Alg_Top_2016.pdf |consulta= 18 de setembre de 2019 |llengua=anglès|publicació=[[Universitat de Notre Dame]]}}</ref> Sobre <math>I^2</math> es defineix la relació d'equivalència <math>(x,0)\mathcal{R} (x,1)</math> i <math>(0,y)\mathcal{R} (1,1-y)</math>. L'espai quocient <math>I^2 /\mathcal{R}</math> és homeomorf a una ampolla de Klein (es difícil de visualitzar ja que no és homeomorf a un subespai de <math>\mathbb{R}^3</math>). |
||
:[[ |
:[[Fitxer:Fundamental_polygon_of_the_Klein_bottle.png|150px|center]] |
||
*L'[[esfera]] com a conjunt quocient:<ref>{{ref-publicació |nom=Chen Hui George Teo |article=Classificació de superfícies |url=http://www.math.uchicago.edu/~may/VIGRE/VIGRE2011/REUPapers/Teo.pdf |consulta= 18 de setembre de 2019 |llengua=anglès|publicació=[[Universitat de Chicago]]}}</ref> Sobre <math>\{(x,y):|x|+|y| \leq 1\}</math> es defineix la relació d'equivalència <math>(x,y)\mathcal{R} (-x,y)</math> per a <math>(x,y)</math> de la [[frontera (topologia)|frontera]]. L'espai quocient corresponent és homeomorf a una esfera. |
*L'[[esfera]] com a conjunt quocient:<ref>{{ref-publicació |nom=Chen Hui George Teo |article=Classificació de superfícies |url=http://www.math.uchicago.edu/~may/VIGRE/VIGRE2011/REUPapers/Teo.pdf |consulta= 18 de setembre de 2019 |llengua=anglès|publicació=[[Universitat de Chicago]]}}</ref> Sobre <math>\{(x,y):|x|+|y| \leq 1\}</math> es defineix la relació d'equivalència <math>(x,y)\mathcal{R} (-x,y)</math> per a <math>(x,y)</math> de la [[frontera (topologia)|frontera]]. L'espai quocient corresponent és homeomorf a una esfera. |
||
Revisió del 02:09, 17 nov 2019

En matemàtiques, la topologia quocient és una topologia definida sobre el conjunt quocient generat per una relació d'equivalència sobre un espai topològic.
Definició
Siga un espai topològic i una relació d'equivalència sobre . El conjunt quocient és el conjunt de les classes d'equivalència dels elements de :
Els conjunts oberts que conforman l'anomenada topologia quocient sobre són els conjunts de las classes d'equivalència les unions de les quals són conjunts oberts en :
Definició equivalent: sigui l'aplicació projecció donada per , aleshores es defineixen els oberts de com els conjunts tals que és obert en .
Propietats
- L'aplicació que envia a cada element a la seva classe d'equivalència corresponent és continua.[1]
- Siguen la projecció i . L'aplicació és continua si, i només si, la composició és continua.[1]
Exemples
- El tor com a conjunt quocient:[1] Sobre es defineix la relació d'equivalència i . L'espai quocient és homeomorf a un tor.
- La cinta de Möbius com a conjunt quocient:[1] Sobre es defineix la relació d'equivalència . L'espai quocient és homeomorf a una cinta de Möbius.
- La ampolla de Klein com a conjunt quocient:[2] Sobre es defineix la relació d'equivalència i . L'espai quocient és homeomorf a una ampolla de Klein (es difícil de visualitzar ja que no és homeomorf a un subespai de ).
- L'esfera com a conjunt quocient:[3] Sobre es defineix la relació d'equivalència per a de la frontera. L'espai quocient corresponent és homeomorf a una esfera.
Vegeu també
Bibliografia
- Robles Corbalá Carlos Alberto, "Topología general", Universitat de Sonora.
- Weisstein, Eric W., «Espai qocient» a MathWorld (en anglès).
- Espai quocient a PlanetMath
Referències
- ↑ 1,0 1,1 1,2 1,3 Llopis, José L. «Espai topològic quocient» (en castellà). Matesfacil. ISSN: 2659-8442 [Consulta: 18 setembre 2019].
- ↑ A. Stolz, Stephan «Topología algebraica» (en anglès). Universitat de Notre Dame [Consulta: 18 setembre 2019].
- ↑ «Classificació de superfícies» (en anglès). Universitat de Chicago [Consulta: 18 setembre 2019].





![{\displaystyle X/{\mathcal {R}}=\{[x]:x\in X\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eba4c149b0eee8162352dcb102a2c4887208c6bf)
![{\displaystyle {\mathcal {T}}_{\mathcal {R}}=\{U\subseteq X/{\mathcal {R}}:\bigcup _{[x]\in U}[x]\subseteq {\mathcal {T}}_{X}\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75e4808dbf758a21b773f2916369efa0cf62bc26)

![{\displaystyle p(x)=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24b8773dff8ad19fc5a8f33134a4da367b04fc0c)







![{\displaystyle I^{2}=[0,1]\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec146272a9e354527468cb89f8213c57e07c937e)