Monodromia
En matemàtiques, monodromia és l'estudi de com els objectes de l'anàlisi matemàtica, topologia algebraica i geometria diferencial es comporten quan 'rodegen' una singularitat. Com el seu nom indica, el significat fonamental de monodromia prové de 'realitzar una ronda individual'. Està estretament relacionat al recobriment d'un mapa i a la seva degeneració en la ramificació corresponent; l'aspecte que dona lloc a fenòmens de monodromia és que certa funció es defineix univaluada quan 'recorrem' una ruta, envoltant alguna singularitat. L'absència de monodromia es mesura mitjançant la definició d'un grup de monodromia: un grup de transformacions que actuen sobre les dades que codifica el que succeeix quan 'envoltem' la singularitat.
Definició[modifica]
Sigui X connex i localment connex, un espai topològic amb base en el punt x, i sigui un recobriment amb fibra . Per un bucle γ:[0,1] → X, on x denota un aixecament sota el mapa de cobertura (des d'un punt de ) per . Finalment, denotem per l'extrem , que és generalment diferent de . Existeixen teoremes que estableixen que aquesta construcció dona una acció de grup ben definida del grup fonamental π1(X, x) de F i que l'estabilitzador de és exactament , és a dir, un element [γ] resol un punt de F si és representada per la imatge d'un circuit en en . Aquesta acció s'anomena acció de monodromia i el corresponent homomorfisme π1(X, x) → Aut (F) en el grup d'automorfismes de F, és la monodromia. La imatge d'aquest homomorfisme és el grup de monodromia.
Exemple[modifica]
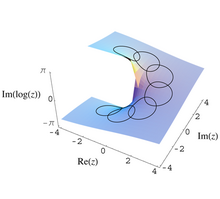
Aquestes idees foren explicitades primer en anàlisi complexa. En el procés de continuació analítica, una funció que és analítica F(z) en un subconjunt obert E del pla complex perforat C \ {0} es pot fer contínua cap a E, però amb valors diferents. Per exemple, prenem
- F(z) = log z
- E = {z ∈ C: Re (z) > 0}
i després estenem analíticament en sentit antihorari al voltant del cercle
- |z| = 0,5
resultarà en el retorn, no a F(z), sinó a
- F(z) + 2 πi.
En aquest cas, el grup de monodromia és cíclic infinit, i l'espai de la coberta és la coberta universal del pla complex foradat. Aquesta coberta pot visualitzar-se com l'helicoide restringit a ρ > 0. El mapa de cobertura és una projecció vertical, en un sentit que col·lapsi l'espiral en la manera òbvia per obtenir un pla perforat.
Equacions diferencials en el domini complex[modifica]
Una aplicació important es troba a les equacions diferencials, on una sola solució pot donar més solucions linealment independents per continuació analítica. Les equacions diferencials lineals definides en un conjunt obert i connex S en el pla complex tenen un grup de monodromia, que és una representació lineal del grup fonamental de S, i que resumeix totes les continuacions analítiques al voltant de bucles dins S. El problema invers, de construir l'equació (amb singularitats regulars), donada una representació, s'anomena problema de Riemann-Hilbert.
Per a un sistema lineal normal (i en particular fuchsià), hom escull generalment com a generadors del grup de monodromia els operadors Mj corresponents als bucles que rodegen un dels pols del sistema en sentit contrari a les agulles del rellotge. Si els índexs j s'escullen de tal manera que augmenten d'1 a p+1 quan hom rodeja el punt base en el sentit de les agulles del rellotge, llavors la relació única entre els generadors és la igualtat . El problema de Deligne-Simpson és el següent problema de realització: Per a quines tuples de classes conjugades a GL(n, C) existeixen tuples irreductibles de matrius Mj d'aquestes classes que satisfacin la relació anterior? El problema ha estat formulat per Pierre Deligne, i Carlos Simpson fou el primer a obtenir-ne resultats cap a la seva resolució. Una versió additiva del problema sobre els residus de sistemes fuchsians ha estat formulada i explorada per Vladimir Kostov. Així, el problema ha estat considerat per altres autors per a grups matricials diferents a GL(n, C).[1]
Aspectes geomètrics i topològics[modifica]
En el cas d'un mapa de cobertura, hom pot veure'l com un cas especial de fibrat, i hom pot utilitzar la propietat d'aixecament d'homotopia per a 'seguir' camins en l'espai base X (suposem que els camins són connexos per simplicitat) quan s'aixequen a la coberta C. Si envoltem un bucle basat en x de X, que aixequem per començar a c sobre x, acabarem en alguns c* novament per sobre de x; és molt possible que c ≠ c* , i per formalitzar aquest canvi hom considera l'acció del grup fonamental π1(X, x) com a grup de permutació de tots els c, com un grup de monodromia en aquest context.
En geometria diferencial, tenen un rol anàleg per transport paral·lel. En un fibrat principal B sobre una varietat diferenciable M, una connexió permet el moviment 'horitzontal' de fibres per sobre m de M a les fibres adjacents. L'efecte quan s'aplica als bucles basats en m, és que defineix un grup d'holonomia de translacions de la fibra a m; si el grup d'estructura de B és G, aquest és un subgrup de G que mesura la desviació de B respecte al fibrat producte M × G.
- Foliacions i monodromia grupoide
De manera anàloga al grupoide fonamental, és possible obviar l'elecció d'un punt base, i definir una monodromia grupoide. Aquí considerem (classes d'homotopia d') aixecaments de camins en l'espai base X d'un fibrat . El resultat té l'estructura d'un grupoide sobre l'espai base X. L'avantatge és que podem baixar la condició de connexió de X.
A més, hom també pot generalitzar la construcció de foliacions: considerem una foliació M (possiblement singular). A continuació, per a cada camí en una fulla de podem considerar el seu difeomorfisme induït en seccions transversals locals a través dels extrems. Dins d'una carta simplement connexa, aquest difeomorfisme esdevé únic i especialment caònic entre seccions transversals diferents, si passem al germen del difeomorfisme al voltant dels extrems. D'aquesta manera, es converteix en independent de la ruta dins d'una carta simplement connexa, i per tant és invariant per homotopia.
Definició a través de la teoria de Galois[modifica]
Sigui F(x) el cos de les funcions racionals en la variable x dins el cos F, que és el cos de fraccions de l'anell de polinomis F[x]. Un element y = f(x) de F(x) determina una extensió finita [F(x) : F(y)].
Aquesta extensió no acostuma a ser de Galois, però té clausura de Galois L(f). El grup de Galois associat a l'extensió [L(f) : F(y)] s'anomena grup de monodromia de f.
En el cas F = C, és present la teoria de la superfície de Riemann, i permet la interpretació geomètrica anterior. En el cas que l'extensió [C(x) : C(y)] sigui de Galois, el grup de monodromia associat s'anomena de vegades grup de transformacions de la coberta.
Referències[modifica]
- ↑ V.P. Kostov «The Deligne–Simpson problem — a survey». J. Algebra, 281, 1, 2004, p. 83–108. i referències internes.
Enllaços externs[modifica]
- V.I. Danilov. Michiel Hazewinkel (ed.). Monodromy. Encyclopedia of Mathematics (en anglès). Springer, 2001. ISBN 978-1-55608-010-4.
- Monodromy a PlanetMath












