Lent tòrica

Una lent tòrica és una lent amb diferent potència òptica i distància focal en dues orientacions perpendiculars entre si. Una de les superfícies de la lent es forma com a superfície "límit" d'un tor de revolució (vegeu el gràfic de la dreta), mentre que l'altra és en general esfèrica. Les lents tòriques s'utilitzen principalment en ulleres, lents de contacte o en una lent intraocular, per corregir l'astigmatisme.[1][2]
Tor de revolució[modifica]
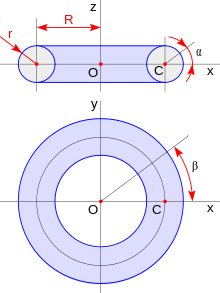
Un tor és el cos espacial que resulta quan un cercle amb radi r gira al voltant d'un eix situat en el mateix pla que el cercle, a una distància R del centre del cercle (figura de la dreta). Si R > r, es produeix un tor d'anell. Si R = r, es produeix un tor de banya, en què l'obertura es contreu a un sol punt. Si R < r es produeix un tor axial, on només queden dos clots de l'obertura, que són menys profunds a mesura que R s'apropa a 0. Quan R = 0, el tor degenera en una esfera amb radi r.[3]

Lent tòrica[modifica]
El radi major de curvatura de la superfície de la lent tòrica, R + r, correspon a la menor potència refractiva, S, donada per
- ,
on n és l'índex de refracció del material de la lent.
El radi menor de curvatura, r, es correspon amb la major potència de refracció, s, donada per
- .
ja que R + r > r, S < s. La lent es comporta aproximadament com una combinació d'una lent esfèrica amb una potència òptica s i una lent cilíndrica amb una potència òptica s − S. En oftalmologia i optometria, a s − S se l'anomena "potència cilíndrica" de la lent. Aquesta combinació s'utilitza per a corregir l'astigmatisme. En aquest context, el terme cilindre es basa en una aproximació matemàtica, que només és vàlida per a les petites potències correctives.[4]
Cal tenir en compte que tant la curvatura major com la menor tenen una secció circular, per tant, en contra del que es podria pensar, la lent tòrica no és un el·lipsoide de revolució.
Funcionament[modifica]
Els raigs de llum dins del pla (x,y)- del tor (com es defineix en la figura anterior) són refractats d'acord amb el radi de curvatura gran, R + r, és a dir, amb la menor potència de refracció,S = (n − 1) / (R + r).
Els raigs de llum dins d'un pla a través de l'eix de revolució (l'eix z) del tor es refracten d'acord amb el radi de curvatura petit, r, és a dir, la major potència de refracció, s = (n − 1) / r. Com a conseqüència, hi ha dos graus de refracció diferents en orientacions perpendiculars entre si. En orientacions intermèdies, els canvis de potència de refracció varien de forma gradual des del valor més gran fins al valor més petit, o a l'inrevés. Això es fa per compensar l'aberració astigmàtica de l'ull.[4]
Lent atòrica[modifica]
Amb les tècniques modernes de disseny, esmerilat i poliment, controlats per ordinador, es poden aconseguir lents amb bones correccions de graduació fins i tot per a amplis angles de visió, ja que permeten generar petites desviacions de la forma tòrica, aquest tipus de lent rep el nom de lent atòrica (literalment, sense lent tòrica). i guarda la mateixa relació amb les lents tòriques que la que té la lent asfèrica amb les lents esfèriques.[5][6]
Vegeu també[modifica]
Referències[modifica]
- ↑ Sunita Agarwal; Athiya Agarwal; Lucio Buratto Textbook of Ophthalmology. Jaypee Brothers Publishers, 2002, p. 209–. ISBN 978-81-7179-884-1.[Enllaç no actiu]
- ↑ Volk, D.: Atoric Lenses, en Duane's Ophthalmology, cap. 50 (Lippinkott, Wilkins & Williams / Wolters-Kluwer Health, Chicago, USA)
- ↑ Weisstein, Eric W., «Torus» a MathWorld (en anglès).
- ↑ 4,0 4,1 Karl Zeiss OPtics:introduction_to_ophthalmic_optics.
- ↑ Meister, D.: Principles of Atoric Lens Design, in: Lens Talk, Vol. 27, No. 3 (Jan. 1998)
- ↑ Clifford W. Brooks. Essentials of Ophthalmic Lens Finishing. Butterworth-Heinemann, 2005. ISBN 978-0-7506-7213-9.


