Retrat de fase

Energia potencial i retrat de fase d'un pèndol senzill. Noti's que l'eix x, que és l'angle del pèndol, es repeteix cada 2π radians.

Il·lustració de com un retrat de fase seria construït pel moviment d'un pèndol senzill.

Retrat de fase de l'equació de van der Pol, .${\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0$

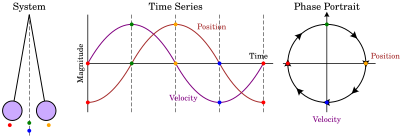
Un retrat de fase és una representació geomètrica de les trajectòries d'un sistema dinàmic en el pla de fase. Cada conjunt de condicions inicials és representat per una corba diferent, o per un punt.

Els retrats de fase són una eina molt útil en l'estudi de sistemes dinàmics. Consisteixen en una representació gràfica de les trajectòries típiques en un espai d'estats. Això revela informació com ara si un punt d'equilibri és atractor, repel·lent o cicle límit segons el valor que s'escolleixi d'un paràmetre. El concepte d'equivalència topològica és important en la classificació del comportament dels sistemes per especificar quan dos retrats de fase diferents representen el mateix comportament dinàmic qualitativament. Un atractor és un punt estable que és també anomenat "embornal" (en anglès, "sink"). Un repel·lent és considerat com un punt inestable i també és conegut com a "font" (en anglès, "source").

Una gràfica del retrat de fases d'un sistema dinàmic descriu les trajectòries del sistema (amb fletxes) i estats estacionaris estables (amb punts) i estats estacionaris inestables (amb cercles) en un espai d'estats. Els eixos representen les variables d'estat.

Exemples

• El pèndol simple, vegeu figura (a la dreta).
• L'oscil·lador harmònic senzill en què el retrat de fase està format per el·lipses centrades a l'origen, que és un punt fix.
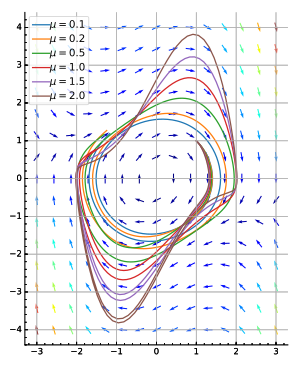
• L'oscil·lador de van der Pol vegi's la figura (a baix a la dreta).

Comportament de Sistemes d'Equacions Diferencials Ordinàries

Un retrat de fase representa el comportament direccional d'un sistema d'EDOs. Del retrat de fase es pot inferir l'estabilitat del sistema.

Estabilitat

Inestable	La majoria de les solucions del sistema tendeixen a ∞ amb el temps
Asimptòticament estable	Totes les solucions del sistema tendeixen a l'origen (0) amb el temps
Neutralment estable	Cap de les solucions del sistema tendeix a ∞ amb el temps, però la majoria de solucions tampoc no tendeixen a 0

Es pot determinar el comportament del retrat de fase d'un sistema d'EDOs a partir dels valors propis o de la traça i el determinant (traça = λ1 + λ2, determinant = λ1 x λ2) del sistema.

Comportament del Retrat de fase

Valors propis, Traça, Determinant	Forma del Retrat de fase
λ1 i λ2 són reals i de signe oposat; Determinant < 0	Sella (inestable)
λ1 i λ2 són reals i del mateix signe, i λ1 ≠ λ2; 0 < determinant < (traça² / 4)	Node (estable si la traça < 0, inestable si la traça > 0)
λ1 i λ2 tenen un component real i imaginari; (Traça² / 4) < determinant	Espiral (estable si la traça < 0, inestable si la traça > 0)

Vegeu també

• Espai de fase
• Pla de fase

Bibliografia

• Jordan, D. W.. Nonlinear Ordinary Differential Equations. fourth. Oxford University Press, 2007. ISBN 978-0-19-920824-1.  Chapter 1.
• Steven Strogatz. Non-linear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering, 2001. ISBN 9780738204536. 

Enllaços externs

• Retrats de Fase lineal, una aplicació matemàtica del MIT.