Teoria de l'aproximació
En matemàtiques, la teoria de l'aproximació estudia com les funcions poden ser aproximades amb altres funcions més simples, incloent la caracterització quantitativa de l'error introduït. Ha de tenir-se en compte que el que s'entén per millor i més simple depèn de l'ús que es vulgui donar a l'aproximació, i dels recursos de càlcul necessaris.[1]
Un tema que hi estretament relacionat és l'aproximació de funcions mitjançant sèries de Fourier generalitzades, és a dir, aproximacions fonamentades en la suma d'una sèrie de termes basats en polinomis ortogonals.[2]
Un problema de particular interès és el d'aproximar una funció en una biblioteca matemàtica d'un ordinador, utilitzant operacions que es poden realitzar fàcilment en el dispositiu (per exemple, la suma i la multiplicació), de manera que el resultat sigui el més proper possible a la funció buscada. Això normalment es fa amb aproximacions polinòmiques o racionals (relació de polinomis).
Així doncs, l'objectiu és fer que l'aproximació sigui el més propera possible a la funció real, generalment amb una precisió (error) propera a la precisió aritmètica en coma flotant de la computadora en qüestió. Això s'aconsegueix mitjançant l'ús d'un polinomi d'alt grau, i/o estrenyent el domini sobre el qual el polinomi ha d'aproximar la funció. La reducció del domini sovint es pot fer mitjançant l'ús de diverses fórmules de suma o escalat per a la funció que s'aproxima. Les biblioteques matemàtiques modernes sovint redueixen el domini en molts segments petits i usen un polinomi de grau baix per a cada segment.
Polinomis òptims[modifica]
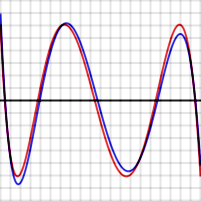
Una vegada que es tria el domini (típicament un interval) i el grau del polinomi, el polinomi en si es tria de tal manera que es minimitzi l'error del pitjor dels casos. És a dir, l'objectiu és minimitzar el valor màxim de , on P(x) és el polinomi de l'aproximació, f(x) és la funció real, i x varia en l'interval triat. Per a funcions amb bon comportament, existeix un polinomi de grau N-èssim que conduirà a una corba d'error que oscil·la entre i un total de N+2 vegades, la qual cosa dona una cota del pitjor resultat de l'error . Existeix un polinomi de grau N-èssim que pot interpolar N+1 punts en una corba. Tal polinomi és sempre òptim. És possible trobar funcions artificials f(x) per les quals no existeix tal polinomi, però rarament se solen donar en la pràctica.[3]
Per exemple, els gràfics situats a la dreta mostren l'error en aproximar log(x) i exp(x) per a N = 4. Les corbes vermelles, per al polinomi òptim, estableixen un nivell de referència, és a dir, oscil·len entre i exactament. Ha de tenir-se en compte que, en cada cas, el nombre d'extrems és N+2, és a dir, 6. Dos dels extrems estan en els punts finals de l'interval, en les vores esquerra i dreta dels gràfics.
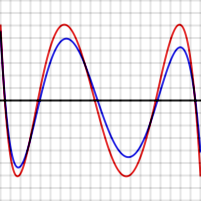
Per demostrar que això és cert en general, suposi's que P és un polinomi de grau N que té la propietat descrita, és a dir, que dona lloc a una funció d'error que té N + 2 extrems, de signes alterns i magnituds iguals. El gràfic vermell a la dreta mostra com podria ser aquesta funció d'error per a N = 4. Suposi's que Q(x) (la funció d'error de la qual es mostra en blau a la dreta) és un altre polinomi de grau N que és una millor aproximació a f que P. En particular, Q està més prop de f que P per a cada valor x<sub>i</sub> on se situa un extrem de P-f, llavors
Quan es produeix un màxim de P-f en xi, llavors
I quan es produeix un mínim de P-f en xi, llavors
Llavors, com es pot veure en el gràfic, [P(x) - f(x)] - [ Q (x) - f(x)] ha d'alternar en el signe de N + 2 valors de xi. Però [P(x) - f(x)] - [ Q (x) - f(x)] es redueix a P(x) - Q(x) que és un polinomi de grau N. Aquesta funció canvia el signe almenys N+1 vegades, per la qual cosa, pel teorema del valor intermedi, té N+1 zeros, la qual cosa és impossible per a un polinomi de grau N.[4]
Aproximació de Txebixov[modifica]
Es poden obtenir polinomis molt propers a l'òptim expandint la funció donada en termes dels polinomis de Txebixov i després tallant l'expansió en el grau desitjat.[5]
Aquest enfocament és similar a l'anàlisi de Fourier de la funció, utilitzant els polinomis de Txebixov en lloc de les funcions trigonomètriques habituals.
Si es calculen els coeficients en l'expansió de Txebixov per a una funció:
i després es talla la sèrie després del terme , s'obté un polinomi de grau N-èssim que s'aproxima a f(x).
La raó per la qual aquest polinomi és gairebé òptim és que, per a funcions amb sèries de potències que convergeixen ràpidament, si la sèrie es talla després d'un terme, l'error total que sorgeix del tall és proper al primer terme després del tall. És a dir, el primer terme després del tall domina respecte tots els termes posteriors. El mateix és cert si l'expansió és en termes d'altres tipus de polinomis. Si una expansió de Txebixov es talla després de , l'error prendrà serà proper a un múltiple de . Els polinomis de Txebixov tenen la propietat que estan anivellats: oscil·len entre +1 i −1 en l'interval [−1, 1]. té N+2 nivells extrems. Això significa que l'error entre f(x) i la seva expansió de Txebixov a és propera a una funció de nivell amb N+2 extrems, per la qual cosa està prop del polinomi òptim de grau N.
En els gràfics anteriors, s'ha de tenir en compte que la funció d'error blau és de vegades millor (és més propera) que la funció vermella, però de vegades és pitjor, la qual cosa significa que no és el polinomi òptim. També, s'ha de notar que la discrepància és menys greu per a la funció exp, que té una sèrie de potències convergent extremadament ràpida, que per a la funció de registre.
L'aproximació de Txebixov és la base de la quadratura de Clenshaw-Curtis, una tècnica d'integració numèrica.[6]
Algorisme de Remez[modifica]
L'algorisme Remez (de vegades escrit Remes) s'usa per produir un polinomi òptim P(x) que s'aproxima a una funció donada f(x) en un interval donat. És un algorisme iteratiu que convergeix a un polinomi que té una funció d'error amb N+2 nivells extrems. Segons el teorema anterior, aquest polinomi és òptim.[7]
L'algorisme de Remez utilitza el fet que es pot construir un polinomi de grau N que condueix a nivells i valors d'error alterns, donats els N+2 punts de referència.
Donats N+2 punts de referència , , ... (on i són presumiblement els punts finals de l'interval d'aproximació), aquestes equacions han de resoldre's:
Els costats de la dreta s'alternen en senyal, és a dir
Atès que , ..., són dades donades, totes les seves potències són conegudes, i , ..., són també coneguts. Això significa que les equacions anteriors són només N+2 equacions lineals en les N+2 variables , , ..., i . Donats els punts de referència , ..., , es pot resoldre aquest sistema per obtenir el polinomi P i el nombre .
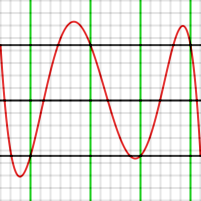
El següent gràfic mostra un exemple d'aquesta configuració, produint un polinomi de quart grau que s'aproxima a sobre el domini [−1, 1]. Els punts de prova es van establir en −1, −0.7, −0.1, +0.4, +0.9 i 1. Aquests valors es mostren en verd. El valor resultant d' és 4.43 × 10−4.
Tingui's en compte que el gràfic d'error pren els valors en els sis punts de prova, inclosos els punts finals, però que aquests punts no són extrems. Si els quatre punts de prova interiors haguessin estat extrems (és a dir, la funció P(x) f(x) hi tingués màxims o mínims), el polinomi seria òptim.
El segon pas de l'algorisme de Remez consisteix a moure els punts de prova a les ubicacions aproximades on la funció d'error tenia els seus màxims o mínims locals reals. Per exemple, en observar el gràfic es pot dir que el punt en −0.1 hauria d'haver estat en aproximadament −0.28. La forma de fer això en l'algorisme és usar un únic pas del mètode de Newton. Com es coneix la primera i la segona derivada de P(x) − f(x), es pot calcular aproximadament fins a quin punt s'ha de moure un punt de prova perquè la derivada sigui zero.
Calcular les derivades d'un polinomi és senzill. També s'ha de poder calcular la primera i la segona derivada de f(x). L'algorisme de Remez requereix la capacitat de calcular , i amb una precisió extremadament alta. Tot l'algorisme ha de dur-se a terme amb major precisió que la precisió desitjada del resultat.
Després de moure els punts de prova, es repeteix el pas de l'equació lineal, obtenint un nou polinomi, i s'utilitza el mètode de Newton una altra vegada per moure els punts de referència novament. Aquesta seqüència continua fins que el resultat convergeix a la precisió desitjada. L'algorisme convergeix molt ràpidament. La convergència és quadràtica per a funcions amb bon comportament: si els punts de prova tenen un error de respecte el resultat correcte, tindran un error d'aproximadament després de la següent iteració.
L'algorisme de Remez generalment s'inicia triant els extrems del polinomi de Txebixov com els punts inicials, ja que la funció d'error final serà similar a aquest polinomi.[7]
Revistes principals[modifica]
Les principals revistes dedicades al tema de laproximació són les següents:
- Journal of Approximation Theory, editada des del juny de 1968.[8]
- Constructive Approximation, editat des del desembre de 1985.[9]
- East Journal on Approximations, editat des del 1995.
Referències[modifica]
- ↑ Approximation Theory, Volumen 36. American Mathematical Soc., 1986, p. X de 131. ISBN 9780821800980.
- ↑ Encyclopaedia of Mathematics (set). Springer Science & Business Media, 1994, p. 155 de 5402. ISBN 9781556080104.
- ↑ Olavi Nevanlinna. Convergence of Iterations for Linear Equations. Birkhäuser, 2012, p. 64. ISBN 97830348854.
- ↑ Nathaniel Max Rock. Standards Driven Math: Calculus. Team Rock Press, 2007, p. 23 de 120. ISBN 9781599800325.
- ↑ Fauziahanim Che Seman. Chebyshev Approximation of Discrete Polynomials and Splines. Kolej Universiti Teknologi Tun Hussein Onn, 2004, p. 75.
- ↑ G. Nurnberger. Multivariate Approximation and Splines. Springer Science & Business Media, 1997, p. 153 de 324. ISBN 9783764356545.
- ↑ 7,0 7,1 Jean-Michel Muller. Elementary Functions: Algorithms and Implementation. Springer Science & Business Media, 2006, p. 41 de 266. ISBN 9783034885478.
- ↑ «Journal of Approximation Theory - Volume 1, Issue 1» (en anglès). ScienceDirect. [Consulta: 15 agost 2022].
- ↑ «Constructive Approximation - Volumes and issues» (en anglès). Springer. [Consulta: 15 agost 2022].
Bibliografia[modifica]
- N. I. Achiezer (Akhiezer), Theory of approximation, Translated by Charles J. Hyman Frederick Ungar Publishing Co., New York 1956 x+307 pp.
Timan, A. F.. Theory of approximation of functions of a real variable (en anglès). Oxford,: Pergamon Press; [distributed in the Western Hemisphere by Macmillan, New York]. ISBN 0-486-67830-X.
- C. Hastings, Jr. Approximations for Digital Computers. Princeton University Press, 1955.
- J. F. Hart, E. W. Cheney, C. L. Lawson, H. J. Maehly, C. K. Mesztenyi, J. R. Rice, H. C. Thacher Jr., C. Witzgall, Computer Approximations. Wiley, 1968, Lib. Cong. 67-23326.
- L. Fox and I. B. Parker. "Chebyshev Polynomials in Numerical Analysis." Oxford University Press London, 1968.
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP. «Section 5.8. Chebyshev Approximation». A: Numerical Recipes: The Art of Scientific Computing. 3rd. New York: Cambridge University Press, 2007. ISBN 978-0-521-88068-8.
- Cody, William James. Software manual for the elementary functions (en anglès). Englewood Cliffs, N.J.: Prentice-Hall. ISBN 0-13-822064-6.
- E. Remes [Remez], "Sur le calcul effectif des polynomes d'approximation de Tschebyscheff". 1934 C. R. Acad. Sci., Paris, 199, 337-340.
- Steffens, Karl-Georg. The history of approximation theory : from Euler to Bernstein (en anglès). Boston: Birkhäuser. ISBN 0-8176-4353-2.
- T. Erdélyi, "Extensions of the Bloch-Pólya theorem on the number of distinct real zeros of polynomials", Journal de théorie des nombres de Bordeaux 20(2008), 281–287.
- T. Erdélyi, "The Remez inequality for linear combinations of shifted Gaussians", Math. Proc. Camb. Phil. Soc. 146(2009), 523–530.
- L. N. Trefethen, "Approximation theory and approximation practice", SIAM 2013. [1]
Vegeu també[modifica]
Enllaços externs[modifica]
- «Història de la teoria de l'aproximació (HAT)]» (en anglès). Arxivat de l'original el 2019-09-18. [Consulta: 22 març 2021].
- «Surveys in Approximation Theory (SAT)» (en anglès).