Usuari:Jordiventura96/proves/Arrel quadrada de 2

Valor de l'arrel de 2 $({\sqrt {2}})$
Decimal	1.4142135623730950488...
Binari	1.0110101000001001111...
Hexadecimal	1.6A09E667F3BCC908B2F...
Fracció contínua	$1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{\ddots }}}}}}}}$
Forma algebraica	${\sqrt {2}}$

L'arrel quadrada de 2 (la línia dels nombres no està a escala).

L'arrel quadrada de 2 (o constant pitagòrica) anotada com ${\sqrt {2}}$ és definit com l'únic nombre algebraic positiu que, multiplicat per si mateix, dóna el nombre 2, altrament dit, √2 × √2 = 2. És un nombre irracional, que té un valor aproximat de:

${\sqrt {2}}\approx 1,414213562373095048801688724209698078569\dots$.

El càlcul del valor aproximat de √2 ha estat un problema matemàtic durant segles. Aquesta recerca ha permès perfeccionar els [[Algorítmica|algoritmes de càlcul d'extracció d'arrels quadrades. En informàtica, han servit per optimitzar dels algoritmes en la reducció del temps de càlcul i el consum de memòria.

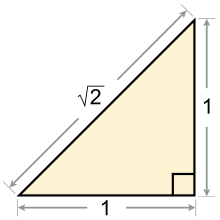
La longitut d'√2 pot ser construïda geomètricament de diverses maneres: per exemple, com la diagonal d'un quadrat de costat la unitat, que és la hipotenusa d'un triangle rectangle issòsceles, val √2 segons el teorema de Pitàgores.

La hipotenusa d'un triangle rectangle issòsceles de costat 1 val √2.

Representació numèrica d'√2.

Amb l'aproximació es pot conèixer un gran nombre de xifres decimals d'aquest número.

L'arrel de dos, també és anomenada constant de Pitàgores en honor al filòsof i matemàtic grec Pitàgores (582 aC - 496 aC), va ser estudiada des de fa molt temps pels babilònics, experts en qüestions de segon grau i disposaven d'un algoritme d'aproximació precís. Des de l'escola de Pitàgores, els grecs del segle v aC i del segle IV aC l'estudien per tal d'entendre millor la incommensurabilitat, concepte equivalent al d'irracionalitat que es coneix actualment. Van trobar fins a tres demostracions diferents de la irracionalitat del nombre, que van conduir a diversos avenços, com el desenvolupament del raonament per l'absurd, el mètode del descens infinit o l'antifèresi, un algoritme comparable a la fracció contínua actual. Per als grecs, ni les fraccions ni els nombres irracionals són nombres. Aquest pas es va donar pels matemàtics àrabs, en el que va ser l'inici a l'àlgebra.

Aquest nombre intervé en diverses aplicacions de la vida quotidiana:

• Els fulls de paper de format internacional (ISO 216) tenen una proporció entre la llargària i l'amplada igual a l'√2.
• En música, la raó entre les freqüències de la quarta augmentada de l'escala temperada val √2.
• En electricitat, la tensió màxima del corrent altern monofàsic domèstic val √2 la tensió eficaç indicat (generalment 110 o 230 V.
• En fotografia, la sèrie de valors d'obertura del diafragma són valors aproximats d'una progressió geomètrica de raó igual a √2.

Història

Període babilònic antic

La tauleta babilònica d'argila YBC 7289 amb anotacions. A part de mostrar l'arrel quadrada de 2 en sexagesimal (1 24 51 10), la tauleta també dóna un exemple en què el costat del quadrat val 30 i la diagonal llavors val 42 25 35. El dígit sexagesimal 30 també pot significar 1/2, en tal cas 42 25 35 és aproximadament 0.7071065.

La cultura matemàtica babilònica va ser, sobretot, algorítmica. Disposava d'un sistema de numeració en notació posicional. Algunes tauletes, com la BM 13901, mostren una bona coneixença de les equacions de segon grau, probablement tractades a partir de mètodes geomètrics simples. Per tal de disposar de mètodes de resolució, els babilonis sabien calcular aproximacions d'arrels quadrades. La tauleta YBC 7289, redactat en el primer terç del segon mil·lenni abans de Crist, dóna una aproximació de l'arrel de dos, interpretada com la raó entre la diagonal d'un quadrat i el costat, sota la forma següent:  :

Aquesta escriptura correspon a la millor aproximació possible d'√2 amb quatre xifres significatives en numeració babilònica (sexagesimal, de base 60).

$1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}=1,41421{\overline {296}}$.

L'aproximació és precisa a la mil·lionèssima. Denota la coneixença d'un algoritme d'aproximació de l'arrel quadrada, pero s'ignora de quin. Podria tractar-se del mètode d'Héron, encara avui en dia un dels més eficaços..

Una altra aproximació antiga a aquest nombre irracional es dóna a l'Antiga Índia en el text matemàtic Baudhaiana-sulba-sutra (d'entre el 600 i el 300 aC) que diu: incrementa la longitut (del costat) per la seva tercera part, i la seva tercera per les seves tre quartes i la seva tercera per la seva trenta-quatrena part de quatre. És a dir:

$1+{\frac {1}{3}}+{\frac {1}{3\cdot 4}}-{\frac {1}{3\cdot 4\cdot 34}}={\frac {577}{408}}\approx 1,414215686.$

Grècia antiga

Els matemàtics de l'antiga Grècia van descubrir i demostrar la irracionalitat de l'arrel de 2, en una època que resulta difícil de determinar, com a molt tard en les primeres dècades del segle IV aC i sembla ser que no abans del segle v aC. Però ells no el van expressar mai d'aquesta forma, com a nombre √2, sinó com una raó (en el sentit de proporció) entre la diagonal i el costat d'un quadrat. I van mostrar com les dues mesures son incommensurables, és a dir, que no es pot trobar un segment unitat, per petit que sigui, que permeti mesurar de manera exacta les dues magnituts.

El descobriment de la irracionalitat, la data, les circumstàncies que van conduir a ella, les seves conseqüències, la naturalesa de les primeres demostracions,... tot això ha generat molt treball entre els historiadors, però no han estat capaços d'arribar a un consens.

No existeixen evidències arqueològiques anàlogues a les tauletes babilòniques pel cas dels matemàtics de l'Antiga Grècia, però sí que s'han trobat textos transmesos per tradició, per còpia i recòpia. Els més antics que han sortit a la llum daten del segle IV aC. Entre aquestes obres, en què les matemàtiques no són l'objectiu principal, hi trobem els treballs de Plató i els d'Aristòtil.

Plató i Aristòtil

En un passatge molt conegut del Menó, Plató posa en escena Sòcrates fent descobrir un jove esclau la duplicació d'un quadrat, mitjançant la construcció d'un quadrat sobre la diagonal de l'original. Sòcrates vol convèncer Ménon que el jove esclau troba un coneixement que ja és en ell mateix (mitjançant la tècnica retòrica coneguda com la maièutica). David Fowler, matemàtic historiador de la matemàtica anglès, data el text al 385 aC i el considera també la primera prova material directa de la pràctica de la matemàtica grega..

La primera menció coneguda de la incommensurabilitat és igualment deguda a Plató, en una obra més tardana, el Teetet, on descriu Teodor de Cirene exposant allò que correspon a la irracionalitat de les arrels quadrades dels nombre del 3 al 17 que no són quadrats perfectes. Es dedueix d'aquest passatge que la irracionalitat de l'√2 ja era coneguda a l'època en què Plató va escriure, i fins i tot durant els anys en què es creu que Théodore s'hauria dedicat a la docència, les primeres dècades del segle IV aC.

A l'Organon, Aristòtil agafa com a exemple la reducció a l'absurd que el condueix a la incommensurabilitat de la diagonal, i precisa (en dues ocasions) que la hipòtesi de la commensurabilitat condueix al fet contradictori que un nombre parell és igual a un nombre imparell. La indicació és poc precisa, però es tracta igualment del primer en tenir una demostració.

Euclides

En el llibre Elements, d'Euclides, el primer tractat de matemàtiques que ens ha arribat escrit al voltant de l'any 300 aC, el tractament de la incommensurabilitat ja és bastant elaborat. Aquest tema és definit i tractat en el llibre X, i la proposició 2 en dóna caracterització a partir d'un procediment de sostraccions iteratives, l'antifèresi, procediment que avui es coneix com l'algorisme d'Euclides (una divisió es pot considerar una sèries de sostraccions) en l'aritmètica i la fracció contínua en els nombres reals. Una longitut és incommensurable mentre hi hagi residu, el procediment continua indefinidament. La proposició 9 permet establir una relació amb les propietats aritmètiques tractades en els llibres VII i VIII. Algunes edicions antigues del llibre X que presenten en un apèndix una proposició (de vegades enumerat 117) que tracta directament de la irracionalitat de l'arrel de dos (de la incommensurabilitat de la raó entre la diagonal d'un quadrat i el seu costat), aportant un argument de paritat i un de descendència infinita. Però aquest article no s'integra en la resta del text, és per això que es creu que ha estat afegit per un interès històric, molt possiblement després d'Euclides. . Sembla ser posterior a una altra demostració, sempre basant-se en un argument de paritat donat en un dels passatges d'Aristòtil citat aquí sota per Alexandre d'Afrodísies el segle ii, el més antic i complet que ens ha arribat amb data (de la incommensurabilitat de la diagonal d'un quadrat respecte el seu costat)..

Hipòtesis i reconstruccions

El que es pot saber sobre el descobriment de la irracionalitat depèn, més enllà dels Elements, dels fragments de textos antics d'autors posteriors, en particular d'una història d'un alumne d'Aristòtil, Eudem de Rodes i més generalment de textos històrics tardans, la fiabilitat dels quals no és bona.

També hi ha diverses teories pel que fa al context i les causes del descobriment de la incommensurabilitat. Pel que fa a les seves primeres manifestacions, els historiadors es limiten a recontruir-les d'una manera coherent segons coneixements que es suposen d'aquella època. Aquestes reconstruccions especulatives, desenvolupades a finals del segle xix i principis del xx, estan lluny de coincidir i han obert sempre el debat.

Sobre √2

Richard Dedekind proposa una construcció rigurosa dels nombres reals a finals del Segle XIX.

La història de l'arrel de dos es confon llavors amb la de l'arrel quadrada i més generalment amb la dels irracionals. Es pot resumir en les següents línies.

Els grecs concebien el que nosaltres anomenem nombres racionals o reals com a proporcions, no com a nombres. La feblesa dels conceptes apareix en igualtats com √2 x √3 = √6. Per als grecs, no és demostrable: √2 x √3 designa una proporció entre àrees i √6 no pertany al món de les àrees. El quadrat d'una superfícies no existeix per als grecs..

La cultura matemàtica aràbica de l'antiguitat és l'origen del següent progrés. A principis del segle ix, el persa Muhàmmad ibn Mussa al-Khwarazmí desenvolupa els conceptes ?d'equació i d'incògnita. Aquests descubriments de vegades són considerats com el naixement de l'àlgebra., conduint gradualment a la idea de donar un estatus de nombre a les fraccions i les proporcions incommensurables. Les propietats algèbriques de les arrels quadrades són establides. Omar Khayyam desenvolupa en el segle xi una teoria on les proporcions són nombres, encara que els incommensurables encara són considerats impropis. Europa n'assimila les nocions tardanament, al segle XVI], període de polèmica sobre si els incommensurables mereixen tenir l'estatus de nombre. És en aquesta època que l'ús del símbol √ es consolida.

Construir un univers de nombres en què la igualtat √2 x √3 = √6 sigui demostrada rigorosament no és fàcil. Aquesta construcció apareixerà tardanament de la mà de Dedekind, l'any 1876.

Propietats

Representació en fracció contínua

L'arrel quadrada de dos està relacionada amb un cert nombre de representacions en fracció contínua periòdica diferents. De manera general, segueixen la següent representació:

$b{\sqrt {2}}-a={\cfrac {-k}{2a+{\cfrac {-k}{2a+{\cfrac {-k}{2a+\ddots }}}}}}\,$

amb a² − 2b² = k, i amb a i b nombres enters estrictament positius. En el cas particular en què a=1, b=1 i k=-1, es té la següent representació:

$\!\ {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}.$

De manera més general, es pot calcular la representació en fracció contínua d'una arrel qualsevol emprant la següent identitat:

${\sqrt {x}}=1+{\cfrac {x-1}{2+{\cfrac {x-1}{2+{\cfrac {x-1}{2+{\ddots }}}}}}}$

que prové de la identitat:

${\sqrt {x}}=1+{\frac {x-1}{1+{\sqrt {x}}}}$

Desenvolupament en producte infinit

La identitat cos(π/4) = sin(π/4) = 1/√2 és la representació en producte infinit del sinus i del cosinus porten als desenvolupaments següents:

${\sqrt {2}}=2\prod _{k=0}^{\infty }{\frac {(4k+1)(4k+3)}{(4k+2)^{2}}}=2\left(1-{\frac {1}{4}}\right)\left(1-{\frac {1}{36}}\right)\left(1-{\frac {1}{100}}\right)\cdots$

${\sqrt {2}}=\prod _{k=0}^{\infty }{\frac {(4k+2)^{2}}{(4k+1)(4k+3)}}=\left({\frac {2\cdot 2}{1\cdot 3}}\right)\left({\frac {6\cdot 6}{5\cdot 7}}\right)\left({\frac {10\cdot 10}{9\cdot 11}}\right)\left({\frac {14\cdot 14}{13\cdot 15}}\right)\cdots$

L'últim producte es pot escriure de manera equivalent:

${\sqrt {2}}=\prod _{k=0}^{\infty }\left(1+{\frac {1}{4k+1}}\right)\left(1-{\frac {1}{4k+3}}\right)=\left(1+{\frac {1}{1}}\right)\left(1-{\frac {1}{3}}\right)\left(1+{\frac {1}{5}}\right)\left(1-{\frac {1}{7}}\right)\cdots .$

Desenvolupament en sèries de Taylor

El número també pot ser donat ne forma de sèrie utilitzant el desenvolupament de Taylor d'una funció trigonomètrica evaluada en $\left({\pi }/{4}\right)$, com es mostra a continuació:

${\frac {1}{\sqrt {2}}}=\sum _{k=0}^{\infty }{\frac {(-1)^{k}\left({\frac {\pi }{4}}\right)^{2k}}{(2k)!}}.$

${\frac {1}{\sqrt {2}}}=\sum _{k=0}^{\infty }{\frac {(-1)^{k}\left({\frac {\pi }{4}}\right)^{2k+1}}{(2k+1)!}}.$

També es pot trobar el valor evaluant la funció $y={\sqrt {1+x}}$ en x=1:

${\sqrt {2}}=1+\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {\prod _{0<n<k}(2n-1)}{\prod _{n=1}^{n=k}(2n)}}=1+{\frac {1}{2}}-{\frac {1}{2\cdot 4}}+{\frac {1\cdot 3}{2\cdot 4\cdot 6}}-{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6\cdot 8}}+\cdots .$

La convergència d'aquesta última sèrie pot ser accelerada mitjançant una transformació d'Euler per donar:

${\sqrt {2}}=\sum _{k=0}^{\infty }{\frac {(2k+1)!}{(k!)^{2}2^{3k+1}}}={\frac {1}{2}}+{\frac {3}{8}}+{\frac {15}{64}}+{\frac {35}{256}}+{\frac {315}{4096}}+{\frac {693}{16384}}+\cdots .$

Grau algebraic i grau d'irracionalitat

L'arrel quadrada de dos és un nombre algebraic de grau 2, anomenat també enter quadràtic, en ser solució de l'equació polinòmica de segon grau a coeficients enters x² − 2 = 0 i de monomi dominant amb coeficient igual a 1 (anomenat habitualment polinomi mònic. No és solució, però, de cap equació de primer grau a coeficients enters, atesa la seva irracionalitat. Se sap, doncs, que és difícilment aproximable per una sèrie racional de tipus p_n/q_n ; segons el teorema de Roth, en el millor dels casos l'error és de l'ordre de:

$\left|{\sqrt {2}}-{\frac {p_{n}}{q_{n}}}\right|\sim {\frac {1}{{q_{n}}^{2}}}$

Com per tot nombre algebraic irracional, la seva mesura d'irracionalitat és 2. La mesura d'irracionalitat (μ) d'un nombre denota quant pròxima és la aproximació que es pot fer a un nombre irracional com a quocient entre dos nombres racionals. És el valor de l'exponent en el denominador de l'expressió següent:

$0<\left|x-{\frac {p}{q}}\right|<{\frac {1}{q^{\mu }}}$

Normalitat

La normalitat és una propietat que es basa en la distribució de les xifres del desenvolupament decimal d'un nombre irracional. Es dóna quan totes les xifres del 0 al 9 en el desenvolupament i amb la mateixa freqüencia. Quant a l'arrel de 2, s'ignora si és normal només en el sistema decimal o si ho és també en totes les altres bases de numeració.

Fórmula de Viète

L'arrel quadrada de dos apareix en la fórmula de Viète per π:

$2^{m}{\sqrt {2-{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}}\to \pi {\text{ as }}m\to \infty \,$

per m arrels quadrades i tansols un signe negatiu (el primer).

Similar en apariència, però amb un nombre finit de termes, l'arrel quadrada de dos apareix en diverses constants trigonomètriques:

$\sin(5{\tfrac {5}{8}}^{\circ })={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}};$

$\sin(11{\tfrac {1}{4}}^{\circ })={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}};$

$\sin(16{\tfrac {7}{8}}^{\circ })={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}}};$

$\sin(22{\tfrac {1}{2}}^{\circ })={\frac {1}{2}}{\sqrt {2-{\sqrt {2}}}};$

$\sin(28{\tfrac {1}{8}}^{\circ })={\frac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}}}};$

$\sin(33{\tfrac {3}{4}}^{\circ })={\frac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}};$

$\sin(39{\tfrac {3}{8}}^{\circ })={\frac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}}};$

$\sin(45^{\circ })={\frac {1}{2}}{\sqrt {2}};$

$\sin(50{\tfrac {5}{8}}^{\circ })={\frac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}}};$

$\sin(56{\tfrac {1}{4}}^{\circ })={\frac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}};$

$\sin(61{\tfrac {7}{8}}^{\circ })={\frac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}}}};$

$\sin(67{\tfrac {1}{2}}^{\circ })={\frac {1}{2}}{\sqrt {2+{\sqrt {2}}}};$

$\sin(73{\tfrac {1}{8}}^{\circ })={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}}};$

$\sin(78{\tfrac {3}{4}}^{\circ })={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}};$

$\sin(84{\tfrac {3}{8}}^{\circ })={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}.$

Altres propietats

La mida de l'angle i l'àrea del sector circular són igual quan el radi cònic té el valor d'arrel quadrada de dos. Aquest diagrama il·lustra les funcions circular i hiperbòlica en funció de les àrees dels sectors u.

La meitat de l'arrel de dos, que és també el seu invers, té un valor aproximat de 0.707106781186548. És una quantitat recurrent en geometria i trigonometria perquè és el valor de cadascuna de les components del vector unitari que té un angle de 45º entre els dos eixos:

$\left({\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}\right).$

Aquest nombre satisfà:

${\tfrac {1}{2}}{\sqrt {2}}={\sqrt {\tfrac {1}{2}}}={\frac {1}{\sqrt {2}}}=\cos(45^{\circ })=\sin(45^{\circ }).$

Una altra propietat interessant de l'arrel quadrada de dos és la següent:

$\!\ {1 \over {{\sqrt {2}}-1}}={\sqrt {2}}+1$

ja que $({\sqrt {2}}+1)({\sqrt {2}}-1)=2-1=1.$ Això està relacionat amb les propietats del nombre platejat,

L'arrel quadrada de dos té també una altra propietat singular que només comparteix amb el número 1 que és que el seu exponencial infinit és igual al seu quadrat. En altres paraules, per c≥1, s'estableix x₁ =c i es defineix x_n+1=c^x_n anomenarem f(c) al límit de la sèrie quan n' tendeixi a infinit:

$\lim _{n\to \infty }x_{n}=f(c)$

Llavors, l'arrel quadrada de dos és l'únic nombre (a part de l'1) que compleix que f(c)=c₂, o expressat de manera simbòlica:

${\sqrt {2}}^{({\sqrt {2}}^{({\sqrt {2}}^{(\ \cdot ^{\cdot ^{\cdot })))}}}}=2.$

L'arrel de dos també es pot expressar en termes de la unitat imaginària $i$ utilitzant només arrels quadrades i operacions aritmètiques:

${\frac {{\sqrt {i}}+i{\sqrt {i}}}{i}}{\text{ o bé }}{\frac {{\sqrt {-i}}-i{\sqrt {-i}}}{-i}}$

Algorisme computacional

Existeixen molts algorismes usats en l'aproximació de l'arrel quadrada de 2. El més comú dels algorismes de computadores o calculadores és el denominat mètode babilònic de càlcul d'arrels quadrades, que és també un dels molts emprats per al càlcul d'altres arrels quadrades. Funciona de de la següent manera:

Es pren en primer lloc un valor arbitrari, que denominarem $F_{0}$; aquesta primera aproximació no importa gaire, només és considerada com un punt d'inici en el algorisme i afecta en quantes iteracions ha de fer l'algorisme fins a obtenir l'aproximació amb la precisió requerida. Llavors, fent servir aquesta suposició inicial, es procedeix a iterar obtenint els nous valors a partir de:

$F_{n+1}={\frac {F_{n}+{\frac {2}{F_{n}}}}{2}}$

Quantes més iteracions es facin mitjançant l'algorisme (és a dir, quants més termes de la sèrie s'obtinguin o quant més gran sigui el subíndex n), s'obtindrà una millor aproximació del valor real de l'arrel quadrada de dos.

L'any 1997, el valor de ${\sqrt {2}}$ va ser calculat mitjançant aquest algorisme fins a 137.438.953.444 xifres decimals per l'equip de Yashumasa Kanada. D'entre les constants matemàtiques amb xifres no periòdiques, només el nombre π ha estat calculat amb millor precisió.

Proves d'irracionalitat

A continuació es mostren algunes de les nombroses demostracions del fet que l'√2 és un nombre irracional. Moltes d'elles es generalitzen substituint √2 per √n on el nombre natural n no és un quadrat perfecte. Algunes són reformulacions amb els conceptes matemàtics i el llenguatge actual de demostracions antigues.

Sovint segueixen procediment de reducció a l'absurd, suposant que √2 és, contràriament, un nombre racional, és a dir, que es pot escriure de la forma p/q, per certs enters q>0 i p. Posteriorment s'arriba a una contradicció a la hipòtesi inicial (√2 = p/q), que també s'escriu com p² = 2q².

Per paritat

Es parteix de la hipòtesi que $\scriptstyle {\sqrt {2}}$ és un nombre racional, és a dir, que es pot expressar com una fracció de nombres enters. Per tant existeixen dos nombres enters positius p i q que compleixen que:

${\frac {p}{q}}={\sqrt {2}}$

Llavors $\scriptstyle {\sqrt {2}}$ pot ser escrit com el valor d'una fracció irreductible (en què el numerador i denominador no tenen divisors comuns) p/q de tal manera que p i q són nombres primers entre sí, i:

${\left({\frac {p}{q}}\right)}^{2}=2\quad \rightarrow \quad p^{2}=2q^{2}$

Per tant, p² és un nombre parell, ja que és igual a 2q². Per tant, p és un nombre parell (ja que els nombres parells només poden tenir arrels quadrades parelles). Atès que p és parell, llavors existeix un nombre r tal que 2r=p. Complint-se doncs la igualtat:

$({2r})^{2}=2q^{2}\quad \rightarrow \quad 4r^{2}=2q^{2}\quad \rightarrow \quad 2r^{2}=q^{2}$

D'on es dedueix que q també és un nombre parell, cosa que contradiu la premissa segons la qual p i q són primers entre ells. En tenir el 2 com a comú divisor, la fracció de p/q no és irreductible, i per tant, $\scriptstyle {\sqrt {2}}$ no pot ser expressada com a quocient de dos nombres enters primers entre ells. L'arrel quadrada de dos no és, per tant, un nombre racional.

Per sostraccions recíproques

Aquesta demostració es basa en la reducció a l'absurd. Es parteix del fet que $\scriptstyle {\sqrt {2}}$ és un nombre racional i que per tant es pot expressar com a fracció de dos nombres enters positius que anomenarem p i q. Es compleix, per tant, que:

${\sqrt {2}}={\frac {p}{q}}\quad \rightarrow \quad 2=\left({\frac {p}{q}}\right)^{2}\quad \rightarrow \quad 2q^{2}=p^{2}$

Si es resta p q a banda i banda d'aquest últim resultat i s'aplica la propietat distributiva, s'obté que:

$2q^{2}-pq=p^{2}-pq\quad \rightarrow \quad q(2q-p)=p(p-q)\quad \rightarrow \quad {\frac {p}{q}}={\frac {2q-p}{p-q}}$

I com que p/q és igual a $\scriptstyle {\sqrt {2}}$, llavors:

${\sqrt {2}}={\frac {2q-p}{p-q}}$

Llavors, com que se sap que p/q és igual a l'arrel de dos:

$1<\left({\frac {p}{q}}\right)^{2}<2\quad \rightarrow \quad 1<{\frac {p}{q}}<2\quad \rightarrow \quad q<p<2q\quad \rightarrow \quad 0<p-q<q$

on en el primer pas s'ha fet l'arrel, en el segon s'ha dividit per q i en el tercer s'hi ha restat q.

Així queda demostrat que p-q és més petit que q, i que numerador i el denominador de la segona fracció igualada a $\scriptstyle {\sqrt {2}}$ són més petits que p i q respectivament. Aquest procediment es pot seguir tants cops com es vulgui, i en cada iteració s'obtenen valors pel numerador i el denominador més petits que en la fracció anterior, creant dues successions infinites estrictament decreixents que han de ser per força enters. Com que això és impossible perquè tota successió infinita estrictament decreixent acabarà tenint valors no enters, queda demostrat que $\scriptstyle {\sqrt {2}}$ és un nombre irracional.

Argument geomètric

Es fonamenta en el mètode de descens infinit. És una construcció geomètrica clàssica de regle i compàs, que prova el teorema d'una manera molt similar a com ho feien els geòmetres grecs.

Sigui ABC un triangle rectangle issòsceles amb hipotenusa de longitut m i catets de longitut n, pel teorema de Pitàgores, n²+n²=m²; 2n²=m²; $\scriptstyle {\sqrt {2}}$ = m/n.

Suposem que m i n són nombre enters.

Es tracen els arcs BD i 'CE amb centre en el punt A. S'uneix DE. Llavors es té que AB=AD, AC=AE i l'angle ∠BAC coincideix amb ∠DAE. Per tant, els triangles ABC i ADE són congruents en tenir dos costats igual i l'angle comprès també.

Com que ∠EBF és un angle recte i ∠BEF és la meitat d'un recte, BEF és també un triangle rectangle issòsceles. Es compleix que BE=BF=m-n. Raonant anàlogament, FDC és també un triangle rectangle issòsceles, amb catets DF=DC=m-n i amb hipotenusa FC=n-(m-n)=2n-m, que són nombres també enters i menors que n i m respectivament. En ser ABC i FDC dos triangles semblants es pot repetir l'anterior procés de forma recurrent i es segueixen obtenint triangles semblant de mides cada cop més petites. Amb les longituts de les hipotenuses i amb la dels catets, s'obtenen dues successions de nombres enters estrictament decreixents que no són finites, la qual cosa és impossible `perquè si n i m són enters ha d'existir una fracció irreductible. Aquesta condició porta a concloure que la suposició que m i n són enters és falsa i que $\scriptstyle {\sqrt {2}}$ no pot ser una fracció $\textstyle {\frac {m}{n}}$ amb m i n enters, per tant, $\scriptstyle {\sqrt {2}}$ ha de ser un nombre irracional

Pel lema d'Euclides

Sigui q l'enter més petit >0 tal que el nombre p=q√2 sigui enter, llavors o q és primer amb p, o és divisor de p². q és doncs igual a 1, i p²=2, cosa que és impossible. Aquest cas, en particular per l'arrel de dos, és un argument general que demostra que l'arrel quadrat d'un enter no quadrat perfecte és irracional.

Pel teorema fonamental de l'aritmètica

Aquest argument parteix del teorema fonamental de l'aritmètica segons el qual per tot nombre enter a diferent de 0, 1 i -1 existeixen nombres primers positius p₁,...p_n tals que a= ± p₁ · p₂ ·...·p_n i són únics llevat de l'ordre.

La parella (p, q) tals que p²=2q², sent aquest cop arbitraris (per exemple, p i q no necessàriament mínims) la contradicció ve del fet que en la descomposició en producte de factors primers, p² té un nombre parell de factors, i 2q² té un nombre imparell. Una variant consisteix a comptar únicament els factors iguals a 2. Aquest argument es pot generalitzar al cas de l'arrel quadrada d'un nombre enter qualsevol que no sigui un quadrat perfecte.

Per congruències

Se sap que en elevar un nombre n al quadrat s'obté un nombre que o bé és divisible per 3, o bé es de la forma 3k+1 (n² és congruent o bé amb 1 o bé amb 0 mòdul 3). Això depèn de si el n és divisible per 3. Si l'arrel de dos és un nombre racional, es pot expressar com la fracció irreductible de dos enters tals que es compleix que:

$a^{2}=2b^{2}$

Llavors a banda i banda de la igualtat no hi pot haver el mateix residu en dividir per 3. S'analitzen a continuació els diferents casos:

• $a^{2}\equiv 0{\pmod {3}};\quad b^{2}\equiv 0{\pmod {3}}\quad \rightarrow \quad .$ Llavors a i b són divisibles per 3 i no són primers entre ells.

• $a^{2}\equiv 0{\pmod {3}};\quad b^{2}\equiv 1{\pmod {3}}\quad \rightarrow \quad .$ Llavors el 2b² és congruent a 2 mòdul 3 i no pot ser igual a a².

• $a^{2}\equiv 1{\pmod {3}};\quad b^{2}\equiv 0{\pmod {3}}\quad \rightarrow \quad .$ Llavors a² no pot ser igual a 2b² perquè a² i 2b² tenen residus diferents en ser dividits per 3.

• $a^{2}\equiv 1{\pmod {3}};\quad b^{2}\equiv 1{\pmod {3}}\quad \rightarrow \quad .$ Llavors a² no pot ser igual a 2b² perquè a² i 2b² tenen residus diferents en ser dividits per 3.

Aquesta demostració es deu al matemàtic argentí Enzo Gentile (1928-1991)

Contruccions geomètriques

Construcció d'√2 amb regle i compàs

Construcció amb regle i compàs.

Com totes les arrels quadrades de nombres enters, √2 és construïble amb regle i compàs; tot i així, no és el cas de l'arrel cúbica de 2, per exemple.

Tingui el segment donat AB longitut unitat, a continuació es tenen els passos a seguir per construir un segment de longitut √2 amb un regle no graduat i un compàs:

1. Trobar el punt B', simètric a B, fent un arc C₁ des del punt A de radi AB i prolongant el costat AB.
2. Traçar la mediatriu [AH] del costat [BB']
   • Traçar un arc C₂ de centre B i radi r>AB.
   • Traçar l'arc C₃ de centre B' i radi r igual al radi usat en el pas anterior. Tallarà l'arc C₂ en el punt H.
   • La distància entre el punt B i el punt C (intersecció de l'arc C₁ i [AH]) és igual a l'arrel de 2.

Construcció de l'√2 només amb compàs

Construcció només amb compàs

Com tot nombre construïble amb regle i compàs, i segons el teorema de Mohr-Mascheroni, √2 és construïble només amb regle. Un possible procediment a seguir en la construcció és:

1. Partint del segment AB de longitut la unitat, traçar els següents arcs de radi AB:
   • L'arc C₁ de centre A.
   • L'arc C₂ de centre B, que tallarà C₁ en dos punts, sigui G un d'ells.
   • L'arc C₃ de centre G, que tallarà C₁ en dos punts, B i H.
   • L'arc C₃ de centre H, que tallarà C₁ en dos punts, G i I.
2. Construir un trianlge ABC que tindrà d'hipotenusa BC=√3 i de catets AB=1 i AC= √2 (Teorema de Pitàgores):
   • Traçar l'arc C₅ de centre I i de radi IG.
   • Traçar l'arc C₆ de centre B i radi BH (=IG), que tallarà C₅ en el punt C.

La longitut del segment AC té una longitut igual a l'√2.

Mètodes numèrics d'aproximació

√2 val aproximadament 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 990 732 478 462 107 038 850 387 534 327 641 572 7

El càlcul d'un valor aproximat a √2 ha estat durant segles una quimera matemàtica. Aquesta recerca ha permès perfeccionar els algorismes de càlcul d'extracció d'arrels quadrades. En informàtica, aquesta recerca es fa per tal d'optimitzar aquests algorismes i reduir el temps de càlcul i el consum de memòria..

Els mètodes numèrics d'aproximació que es presenten a continuació són destinades al càlcul d'un nombre significatiu de xifres decimals. Es basen generalment en successions convergents de nombres racionals. Les millors aproximacions per sèries racionals del tipus p_n/q_n donrn un error de l'ordre de 1/q_n².

Mètodes de convergència lineal

Mètode de Théon de Smyrne

Es deuen al matemàtic grec Teó d'Esmirna les sèries (p_n) i (q_n) definides per les recurrències:

p_{n + 1} = p_n + 2q_n,     p₀ = 1 ;

q_{n + 1} = p_n + q_n,     q₀ = 1.

Els termes de les sèries tenen valors enters estrictament positius, atès que són estricatament creixents, complint que:

p_n² − 2q_n² = (−1)ⁿ(p₀² − 2q₀²)

de manera que p_n/q_n tendeix a √2 per valors grans de n.

No se sap si la intenció de Teó d'Esmirna era la de calcular un valor aproximat a l'arrel de 2.

Solucions a l'equació diofàntica a²− 2b² = k

Les solucions enteres de l'equació a² − 2b² = k són generades a partir de la iteració:

a_{m + 1} = 3a_m + 4b_m

b_{m + 1} = 2a_m + 3b_m

a partir dels valors inicials (a₀, b₀) = (1, 1) per k = −1 i (3, 2) per k = 1. a partir dels valors inicials(a₀, b₀) = (1, 1) per k = −1 i (3, 2) per k = 1.

Aquest mètode és deduït del de Théon: cada iteració d'aquesta correspon a dues de la de Théon. Per tant, a_n /b_n tendeix linealment a l'√2.

Les primeres solucions són:

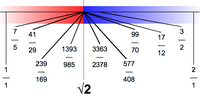
• k = −1 :  (1, 1),  (7, 5),  (41, 29),  (239, 169),  (1393,985),
• k =   1 :  (3, 2),  (17, 12),  (99, 70),  (577, 408),  (3363, 2378).

Les dues aproximacions en negreta van ser utilitzades pels agrimensors antics:

• 28 : 20  (o 7 : 5) amb un error relatiu del –1,0051 %, va ser breument usada a principis del tercer mil·lenni abans de Crist pels egipcis antics.
• 99 : 70  amb un error relatiu de +0,0051 %, al llarg de la història i en molts països en la triangulació racional del quadrat segons els agrimensors.

Mètode de Theon generalitzat

Es donen a i b obtinguts mitjançant el mètode de Théonm que són, doncs, solucions d'una de les dues equacions diofàntiques 2b²=a²–k, amb k=±1 i K>1. Es pot, llavors escriure:

${\sqrt {2}}={\frac {a}{b}}{\sqrt {\frac {K}{(K+k)}}}$

Les sèries p_n i q_n definides per:

$p_{n+1}=(2K+k)p_{n}+2Kq_{n},\quad p_{0}=1;$

$q_{n+1}=(2K+2k)p_{n}+(2K+k)q_{n},\quad q_{0}=1.$

verifiquen que:

$(K+k)p_{n+1}^{2}-Kq_{n+1}^{2}=(K+k)p_{n}^{2}-Kq_{n}^{2}=\dots =k;$

llavors, de la mateixa manera que més amunt, la sèrie p_n/q_n convergeix a $\scriptstyle {\sqrt {K/(K+k)}}$=(b/a)$\scriptstyle {\sqrt {2}}$. A més, si k=1, aquesta sèrie és creixent i s'apropa a aquest valor per defecte; i si k=-1, és decreixent i s'apropa doncs al valor per excés.

Es pot utilitzar aquesta relació per estimar l'error, que ve donat per:

$\epsilon _{n+1}\approx \epsilon _{n}{(4K+3k)}^{-2}$

és un augment si k=1. La convergència és doncs lineal: es guanya una xifra decimal de la constant per a cada iteració.

Aquest mètode correspon a una generalització del mètode del paràgraf anterior al radical $\scriptstyle {\sqrt {K/(K+k)}}$. Per valor molt gran de K, la sèrie (q_n) creix més ràpidament, doncs la convergència és accelerada.

Primeres aproximacions d'√2 = 17/12 √(288/289) per aproximació lineal d'√(288/289). Els paràmetres són a = 17, b = 12, K = 288, k = 1. Es té
ε_{n + 1} < 7,5 × 10^-7ε_n   (abans aproximació decimal de quocients).

Iteració	Valor fraccionari	Decimals exactes
0	1	1
1	19.601/13.860	1,414 213 56
2	22.619.537/15.994.428	1,414 213 562 373 09
3	26.102.926.097/18.457.556.052	1,414 213 562 373 095 048 80
4	30.122.754.096.401/21.300.003.689.580	1,414 213 562 373 095 048 801 688 72

Desenvolupament en fracció contínua

Un altre mètode consisteix a aproximar b√2 - a per la seva fracció contínua generalitzada per valors de a i b solucions de l'equació diofàntica 2b² = a² – k, amb k = ± 1 :

b√2 − a = [0; –k, 2a; –k, 2a; –k, 2a…]

és aproximat amb l'ajuda de la sèrie (p_n/q_n) determinada per la relació de recurrència:

p_{n + 1} = q_n

q_{n + 1} = 2aq_n + kp_n

L'error verifica asimptòticament:

$\epsilon _{n+1}<{\frac {\left|b{\sqrt {2}}-a\right|}{({2a-1})\epsilon _{n}}}$

Primeres aproximacions d'√2 per aproximació lineal de 169√2 − 239. Els paràmetres són b = 169, a = 239, k = 1, ε_{n + 1} ~ 4 × 10⁻⁶ ε_n.

Iteració	Valor fraccionari	Decimals exactes
0	1	1
1	114.243/80.782	1,414 213 562
2	54.608.393/38.613.965	1,414 213 562 373 09
3	26.102.926.097/18.457.556.052	1,414 213 562 373 095 048 80
4	12.477.253.282.759/8.822.750.406.821	1,414 213 562 373 095 048 801 688 7

Desenvolupament en sèrie entera

Es donen a i b solucions de l'equació diofàntica 2b²=a²–k=K, amb k=±1. Es pot, llavors escriure $\scriptstyle {\sqrt {K/(K+''k'')}}$ com a suma d'una sèrie a través del desenvolupament en sèrie de potències enteres de (1+z)^-1/2:

${\sqrt {\frac {\mathrm {K} }{\mathrm {K} +k}}}=1-{\frac {1}{2}}{\frac {k}{\mathrm {K} }}+{\frac {1\times 3}{2\times 4}}\left({\frac {k}{\mathrm {K} }}\right)^{2}-{\frac {1\times 3\times 5}{2\times 4\times 6}}\left({\frac {k}{\mathrm {K} }}\right)^{3}+\dots$

Amb K = 50, i llavors $\scriptstyle {\sqrt {2}}$ = (7/5)$\scriptstyle {\sqrt {50/49}}$, els primers termes de la sèrie són particularment simples, com ja va notar Leonhard Euler, el 1755:

${\sqrt {2}}={\frac {7}{5}}\left(1+{\frac {1}{100}}+{\frac {1\times 3}{1\times 2}}10^{-4}+{\frac {1\times 3\times 5}{1\times 2\times 3}}10^{-6}+\dots \right)=1,4+0,014+0,00021+0,0000035+\dots$

Aproximació √2 = (239/169)$\scriptstyle {\sqrt {57122/57121}}$ pel desenvolupament en sèrie d'enters del radical fraccional. Els paràmetres són b = 239, a = 169, K = 57122, k = –1.

Iteració	Valor fraccionari	Decimals exactes
$0$	$1$	$1$
$1$	${\frac {239}{169}}$	$1,4142$
$2$	${\frac {6238763163557}{4411471739168}}$	$1,41421356237309$
$3$	${\frac {712741258857407103}{503984177369508992}}$	$1,414213562373095048$
$4$	$.\quad {\frac {325705649507622468308893}{230308673437608741128192}}\quad .$	$.\quad 1,414213562373095048801688\quad .$

Dicotomia

És possible aproximar el valor d'arrel de 2 mitjançant el mètode de bisecció. El mètode consisteix en un algoritme de recerca d'arrels que treballa dividint l'interval a la meitat i seleccionant el subinterval que conté l'arrel. Aquest mètode és de convergència lineal lenta, ja que es guanyen només tres decimals per a cada deu iteracions.

Mètodes de convergència quadràtica

El mètode de Newton aplicat a la funció arrel quadrada permet calcular el valor aproximat de √2 de manera iterativa amb una convergència quadràtica, és a dir doblant el número de xifres significatives per a cada iteració. La recurrència té la forma:

$u_{n+1}={\frac {u_{n}}{2}}+{\frac {1}{u_{n}}}$

Aquest algoritme es diu mètode d'Héron o mètode babilònic ja que sembla que va ser aquest el que van utilitzar els babilonis per trobar els valors aproximats de les arrels quadrades.

Si es vol aproximar el valor d'√2 a fraccions successives p/q a partir dels valors inicials p₀=1 i q₀=1, les recurrències de numerador i denominador són:

p_{n + 1} = p_n² + 2q_n²

q_{n + 1} = 2p_nq_n

Primeres aproximacions d'√2 obtingudes amb fraccions successives.

Iteració	Valor fraccionari	Decimals exactes
0	1/1	1
1	3/2	1
2	17/12	1,41
3	577/408	1,41421
4	665857/470832	1,41421356237
5	886731088897/627013566048	1,41421356237309504880168

Mètodes cúbics

Mètode de Halley

Un exemple de màtode cúbic s'obté a partir de la iteració de Halley. Es busca el zero de la funció ƒ(x ) = x² − 2 utilitzant les dues primeres derivades. La solució iterativa és:

x_{n + 1} = x_n × (x_n² + 6)/(3x_n² + 2)

si definim:x_n = p_n/q_n :

p_{n + 1} = p_n(p_n² + 6q_n²)

q_{n + 1} = q_n(3p_n² + 2q_n²)

Aquest mètode és de convergència cúbica, és a dir, per cada iteració el nombre de decimals exactes es triplica.

Primeres aproximacions d'√2 donades pel mètode cúbic.

Iteració	Valor fraccionari	Decimals exactes
0	1	1
1	7/5	1,4
2	1.393/985	1,414 213
3	10.812.186.007/7.645.370.045	1,414 213 562 373 095 048
4	—	1,414 213 562 373 095 048 8 016.887.242.096.980.785.000 718.753.769.480.731.800.000

Mètode de Householder

La iteració de Householder aplicada a ƒ(x ) = 1/x ² − 1/√2 dóna una sèrie convergent a 1/√2 :

x_{n + 1} = x_n + x_n/8 × (2x_n² − 1)(6x_n² − 7)

Mètodes d'ordre superior

S'utilitza un mètode de Newton modificat per trobar el zero de la funció ƒ(x ) = 1/x ² − 1/2. Aquesta dona la sèries recurrent següent:

x_{n + 1} = x_n + x_n/16 × (8h_n + 6h_n² + 5h_n³)

amb:

h_n = 1 − x_n²/2

Aquest mètode és de convergència quàrtica, és a dir de grau 4. El nombre de xifres signifactives correctes es quadrublica a cada iteració.

Primeres aproximacions de l'√2 obtingudes amb el mètode quàrtic.

Iteració	Valor fraccionari	Decimals exactes
0	3/2	1
1	23.169/214	1,414
2	57.367.317.478.181.000.000.000.000.000.000/2105	1,414 213 562 373 09
3	[...]	1,414 213 562 373 09 5.048.801.688.724.209 6.980.785.696.718.753 76.948.073.176.679.740

Existeixen mètodes d'aproximació d'ordre superior, especialment mitjançant els mètodes de Householder.

Altres constants relacionades

Constant de Gelfond-Schneider

Article principal: Constant de Gelfond-Schneider

La constant de Gelfond-Schneider, també anomenada nombre de Hilbert és igual a:

$2^{\sqrt {2}}=2.6651441426902251886502972498731\ldots ,$

que és un nombre transcendent, segons va demostrar el matemàtic rus Rodion Kuzmin l'any 1930. L'any 1934, Alexandr Gelfond va demostrar mitjançant el teorema de Gelfond-Schneider, el cas general de potències elevades a nombres irracionals algebraics, solucionant part del setè dels problemes de Hilbert. Rep el nom dels matemàtics Theodor Schneider i Alexander Gelfond.

La constant de Gelfond-Schneider té com a fracció contínua és: $2^{\sqrt {2}}=[2;1,1,1,72,3,4,1,3,2,1,1,1,14,1,2,1,1,3,1,3,...]$

Nombre platejat

Article principal: Nombre platejat

El nombre platejat (δs) és una constant matemàtica que ve definida com:

$\delta _{s}=1+{\sqrt {2}}$

Té la peculiaritat de tenir com a únic coeficient en la representació de fracció contínua el nombre 2, és a dir:

$\delta _{S}=2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}\,.$

És un nombre irracional algebraic arrel del polinomi:

$({x-1})^{2}-2=0$

√2 en altres àmbits

Astrofísica

En astrofísica, es defineix la velocitat d'un cos en una òrbita circular com:

$v={\sqrt {GM \over {r}}}$

on G és la constant de la gravitació, M és la massa de l'astre que crea el camp gravitatori i r és la distància entre el centre de masses del cos i l'astre respecte el qual s'orbita.

Un altre concepte relacionat és el de la velocitat d'escapament (v_e), que es defineix com la velocitat mínima que un cos necessita per poder escapar de l'atracció del camp gravitatori. Ve definida com:

$v_{e}={\sqrt {\frac {2GM}{r}}}={\sqrt {2}}{\sqrt {\frac {GM}{r}}}={\sqrt {2}}v$

Això vol dir que la velocitat d'escapament és exactament ${\sqrt {2}}$ vegades la velocitat del cos quan es manté a una òrbita circular.

Format del paper

Article principal: Mida de paper

La raó entre la longitut i l'amplada d'un full de format A és una bona aproximació de l'√2.

Els formats de paper A, B i C estàndard ISO 216 van ser dissenyats per comprovar una propietat singulgar: un full tallat en dues parts iguals per la longitut, produeix dos fulls semblants a l'original; és a dir, amb la mateixa proporció entre els seus costats diferents. Sent l'àrea disminuïda en un factor de 2. Això només es dóna quan la raó val √2; en la pràctica les dimensions són aproximades.

A continuació es mostren els valors aprocimats dels formats A0 fins el A6 en funció d'√2.

Valors aproximats de les dimensions dels formats A0 fins el A6 expresats en funció d'√2.

Format	Longitut (m)	Amplada (m)	Àrea (m2})
A0	${\sqrt {\sqrt {2}}}$	${\frac {\sqrt {\sqrt {2}}}{\sqrt {2}}}$	$1$
A1	${\frac {\sqrt {\sqrt {2}}}{\sqrt {2}}}$	${\frac {\sqrt {\sqrt {2}}}{2}}$	${\frac {1}{2}}$
A2	${\frac {\sqrt {\sqrt {2}}}{2}}$	${\frac {\sqrt {\sqrt {2}}}{2{\sqrt {2}}}}$	${\frac {1}{4}}$
A3	${\frac {\sqrt {\sqrt {2}}}{2{\sqrt {2}}}}$	${\frac {\sqrt {\sqrt {2}}}{4}}$	${\frac {1}{8}}$
A4	${\frac {\sqrt {\sqrt {2}}}{4}}$	${\frac {\sqrt {\sqrt {2}}}{4{\sqrt {2}}}}$	${\frac {1}{16}}$

Les sèries B i C difereixen a la sèrie A amb un factor d'√√2 (~ 1,19) i √√√2 (~1,09) respectivament.

Els factors d'expansió del 200%, el 141%, el 71%, el 50% proposats per les fotocopiadores són aproximacions de (√2)ⁿ que permeten passar a formats superiors i inferiors, ja sigui físicament o per impressió de 2ⁿ pàgines per full.

Noti's que en matemàtiques, s'escriu de manera més còmode ${\sqrt {\sqrt {2}}}={\sqrt[{4}]{2}}=2^{1/4}$ i ${\sqrt {\sqrt {\sqrt {2}}}}={\sqrt[{8}]{2}}=2^{1/8}$.

Música

La gamma de temperament igual es construeix així: la raó de proporció entre les freqüències de les notes extremes de l'octava i l'escala és dividida en dotze semitons sent la raó entre les freqüències de dues notes consecutives qualssevol ƒ. La raó de freqüències entre la nota més alta i la més baixa en una octava és doncs ƒ ¹² que val, com s'indica a continuació, 2. El semitò té, doncs, una raó de ƒ = 2^1/12.

Raons de freqüències de les notes de l'escala repecte la freqüèncica més baixa.

do

do♯

ré

ré♯

mi

fa

fa♯

sol

sol♯

la

la♯

si

do

1

21/12

21/6

21/4

21/3

25/12

√2

27/12

22/3

23/4

25/6

211/12

2

En aquest sistema, la quarta augmenntada (Do-Fa♯) i la quinta disminuïda (Do-Sol♭) són iguals i valen sis semitons. Tenen un ratio de freqüències d'√2. En el cant gregorià s'utilitza aquest interval, el tríton. Tot i així, a finals de l'edat mitjana, l'interval és sistemàticament evitat ja que es considera massa dissonant. Va rebre, llavors, el nom de « Diabolus in Musica».

Electricitat

Tensió sinusoïdal : valor eficaç.

En electricitat, la tensió eficaç U_ef d'un corrent altern sinusoïdal monofàsic (per exemple, els 110 V o els 220 V de corrent domèstic) esta relacionada amb l'amplitud de la tensió màxima U_max segons:

U_max = U_eff√2, també anotat Û=U√2,

o, en les aplicacions més comunes:

U_eff = 0,7 U_max.

Aquesta expressió és vàlida en general, pels valors efiacaços de mides lineals d'una ona sinusoïdal. Noti's també que:

20 log (U/√2) = 20 log U - 20 log √2 = 20 log U - log ((√2)²⁰) = 20 log U - log 1.024 ≃ 20 log U - 3.

Es parla d'ample de banda a -3 decibels.

Fotografia

Diafragma controlant l'obertura d'una càmera de fotos.

Article principal: Número f

Les obertures de les càmeres fotogràfiques segueixen la seqüència normalitzada f/1,4, f/2 f/2,8 f/4 f/5,6 f/8 f/11 f/16 f/22, f/32, etc. La raço entre dues obertures consecutius és un valor proper a l'arrel de dos, que ha estat triat de tal manera que la raó de proporció del flux lluminós sigui del voltant de dos (ja que el flux és proporcional al quadrat del diàmetre). En disminuir l'obertura, es dobla el temps d'exposició necessària o disminueix amb un factor 2 la sensibilitat de la pel·lícula necessària.

A la pràctica, l'obertura indicada és un arrodoniment; l'obertura real pot estar més a prop de ${\sqrt {2}}$. Existeixen subdivisions en les càmeres modernes, sovint amb raons de proporció de ${\sqrt {\sqrt {2}}}$ o de ${\sqrt {2}}^{\frac {1}{3}}$.

Relació entre la obertura, el diàmetre del diafragma i el flux lluminós rebut a temps d'exposició i sensibilitats fixades.

Obertura	f/1,4	f/2	f/2,8	f/4	f/5,6	f/8	f/11	f/16	f/22	f/32
Diàmetre	d	d/√2	d/2	d/2√2	d/4	d/4√2	d/8	d/8√2	d/16	d/16√2
Flux	I	I/2	I/4	I/8	I/16	I/32	I/64	I/128	I/256	I/512

Bibliografia

• Flannery, David. The Square Root of Two. Springer, 2005. ISBN 0-387-20220-X. 
• Fowler, David; Eleanor Robson «Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context». Historia Mathematica, 25, 4, novembre 1998, pàg. 366-378.
• Gourdon, X. & Sebah, P. Pythagoras' Constant: √2. Inclou informació de com calcular els dígits d'√2.
• Weisstein, Eric W., «Pythagoras's Constant» a MathWorld (en anglès).
• Benoît Rittaud, Le Fabuleux Destin de √2, Le Pommier, 2006, ISBN 2746502755
• Bertrand Hauchecorne et Daniel Suratteau, Des mathématiciens de A à Z, Ellipses ISBN 978-2729846831
• Gardner, Martin. A K Peters, Ltd.. A Gardner's Workout: Training the Mind and Entertaining the Spirit (en anglès), 2001. ISBN 978-1-56881120-8. .

Història

• Henderson, David W., Square Roots in the Sulbasutra
• Caveing, Maurice. Presses universitaires du Septentrion. La figure et le nombre, 1998, p. 33-75. ISBN 978-2-85939494-3. 
• Denis Daumas, « Sur la démonstration de l’irrationalité chez les grecs », in La démonstration mathématique dans l’histoire, IREM de Lyon
• Fowler, David. Clarendon Press (Oxford Science Publications). The Mathematics of Plato’s Academy (en anglès), 1999. Fowler1999. ISBN 0 19 850258 3. 
• Wilbur Richard Knorr. D. Reidel Publishing Company. The Evolution of the Euclidean Elements A Study of the Theory of Incommensurable Magnitudes and its Significance for Early Greek Geometry (en anglès), 1975, p. 374. Knorr1975. ISBN 90 277 0509 7. 
• Studies on proportion theory and incommensurability (introduction) (en anglès). ISBN 978-90-481-5850-8. .
• (anglès) Árpád Szabó, The Beginnings of Greek Mathematics, Springer, 1978 ISBN 978-9027708199.