Axioma de Pasch

L'axioma de Pasch és el resultat de la geometria plana usada per Euclides, encara que no pot derivar dels seus postulats. El seu paper axiomàtic va ser descobert per Moritz Pasch. Pasch publicà aquest axioma el 1882 i va mostrar que els axiomes d'Euclides eren incomplets. En altres tractaments de la geometria elemental, l'axioma de Pasch és un teorema que es demostra a conseqüència del postulat de separació del pla. L'axioma de Pasch és diferent del teorema de Pasch. L'axioma enuncia que, en el pla, una recta que intersecta amb una aresta d'un triangle i evita els tres vèrtexs ha d'intersecar amb una de les altres dues arestes.

Enunciat

Dues línies (en negre) que intersecten un costat d'un triangle internament i els altres costats internament i externament

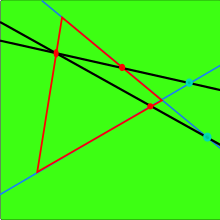
L'axioma afirma que

Axioma de Pasch Siguin A, B i C tres punts que no estan sobre una recta, i sigui a una recta del pla ABC que no passa per cap dels punts A, B, C. Si la recta a passa per un punt del segment AB, també passa per un punt del segment AC, o per un punt del segment BC.

El fet que la recta a no intersecta alhora els segments AC i BC es demostra en el capítol Supplement I,1, escrit per P. Bernays.

Una versió més moderna d'aquest axioma és la següent:

Axioma de Pasch En el pla, si una recta intersecta un costat d'un triangle internament, llavors intersecta exactament un altre costat internament i l'altre costat externament, si no passa per un vèrtex del triangle.

(En el cas que el tercer costat sigui paral·lel a la recta inicial, considerem una "intersecció a l'infinit" com a externa.) Encara es pot trobar una versió més informal d'aquest axioma:

Si una recta no passa per cap vèrtex d'un triangle, i n'intersecta un costat, llavors també n'intersecta un altre costat.

Història

Pasch publicà aquest axioma l'any 1882, i demostrà que els axiomes d'Euclides eren incomplets. L'axioma era part de l'aproximació de Pasch a la introducció de d'ordre dins de la geometria del pla.

Equivalències

En altres tractaments de la geometria elemental, emprant un conjunt diferent d'axiomes, l'axioma de Pasch es pot demostrar com a teorema; és una conseqüència de l'axioma de separació del pla quan es considera com un dels axiomes. Hilbert utilitza l'axioma de Pasch en el seu tractament axiomàtic de la geometria euclidiana. Donats els axiomes restants en el sistema de Hilbert, es pot demostrar que l'axioma de Pasch és lògicament equivalent a l'axioma de la separació del pla.

Ús de Hilbert de l'axioma de Pasch

David Hilbert utilitza l'axioma de Pasch en el seu llibre Fonaments de Geometria, que proporciona una base axiomàtica per a la geometria euclidiana. Depedent de l'edició, es numera com a II.4 o com a II.5.

En el tractament que fa Hilbert, aquest axioma apareix en la secció que fa referència als axiomes d'ordre, i s'hi refereix com a axioma pla d'ordre. Com que no expressa la frase en termes de costats d'un triangle (considerats com a rectes en comptes de segments), no hi ha cap necessitat de parlar sobre interseccions internes i externes de la recta a amb els costats del triangle ABC.

Observacions

L'axioma de Pasch és diferent del teorema de Pasch, que és un resultat sobre l'ordre de quatre punts sobre una recta. Tot i això, en la literatura hi ha moltes ocasions en què l'axioma de Pasch es menciona com a teorema de Pasch. Una d'aquestes aparicions és Greenberg 1974, p. 67.

Cal no confondre l'axioma de Pasch amb l'axioma de Veblen-Young per a la geometria projectiva, que es pot enunciar com:

Axioma de Veblen-Young Si una recta intersecta dos costats d'un triangle, llavors també intersecta el tercer costat.

No hi ha cap menció a interseccions internes i externes en l'enunciat de Veblen-Young, que només té a veure amb la propietat d'incidència de les rectes que s'intersecten. En geometria projectiva, no és vàlid el concepte de què un objecte estigui entre altres dos (necessari per definir intern i extern), i totes les rectes es tallen (de tal manera que no existeix el problema de les dues rectes paral·leles).

Bibliografia

• Beutelspacher, Albrecht; Rosenbaum, Ute. Projective geometry: from foundations to applications. Cambridge University Press, 1998. ISBN 978-0-521-48364-3. 
• Davis, Philip J.; Hersh, Reuben. The Mathematical Experience. Mariner Books, 1999, p. 160. ISBN 0395929687. 
• Faber, Richard L. Foundations of Euclidean and Non-Euclidean Geometry. Nova York: Marcel Dekker, Inc., 1983. ISBN 0-8247-1748-1. 
• Greenberg, Marvin Jay. Euclidean and Non-Euclidean Geometries/Development and History. San Francisco: W.H. Freeman, 1974. ISBN 0-7167-0454-4. 
• Hilbert, David. The Foundations of Geometry [Grundlagen der Geometrie]. Lasalle, IL: Open Court Publishing, 1950 (traducció a l'anglès de E. J. Townsend). 
• Hilbert, David. Foundations of Geometry. LaSalle, IL: Open Court Publishing, 1971. ISBN 0-87548-164-7.  (traducció d'Unger)
• Moise, Edwin. Elementary Geometry from an Advanced Standpoint. Third Edition. Reading, MA: Addison-Wesley, 1990, p. 74. 
• Pambuccian, Victor «The axiomatics of ordered geometry: I. Ordered incidence spaces.». Expositiones Mathematicae, 29, 2011, pàg. 24-66.
• Wylie,Jr., C.R.. Foundations of Geometry. Nova York: McGraw-Hill, 1964. 

Enllaços externs

• Weisstein, Eric W., «Pasch s Axiom» a MathWorld (en anglès).