Llenguatge regular

De la Viquipèdia, l'enciclopèdia lliure

En matemàtiques, lògica i complexitat computacional un llenguatge formal és un llenguatge regular si es pot expressar usant expressions regulars.[1][2][3]

També es pot definir un llenguatge regular com aquell que reconeix un autòmat finit. L'equivalència entre les expressions regulars i autòmats finits es demostra al teorema de Kleene. Aquest tipus de llenguatges s'etiqueten com de tipus 3 en la jerarquia de Chomsky dels llenguatges formals.

Els llenguatges regulars son força útils en l'anàlisi d'entrades i el disseny de llenguatges de programació.

Definició formal[modifica]

La col·lecció de llenguatges regulars sobre un alfabet Σ es defineix recursivament com:

  • El llenguatge buit Ø i la cadena buida {ε} son llenguatges regulars.
  • Per cada a ∈ Σ, el conjunt unitari {a} és un llenguatge regular.
  • Si A i B son llenguatges regulars, llavors A ∪ B (unió), A • B (concatenació), i A* (Clausura de Kleene) son llenguatges regulars.
  • Cap altre llenguatge sobre Σ és regular.

Veieu Expressio regular per la seva sintaxi i semàntica.

Exemples[modifica]

Tots els llenguatges finits son regulars. En particular el llenguatge buit {ε} = Ø és regular. Altres exemples típics consisteixen en el llenguatge format per totes les cadenes sobre un alfabet {a, b} que contenen un nombre parell de as o el llenguatge consistent en totes les cadenes de les formes: moltes as seguides de moltes bs.

Un exemple senzill d'un llenguatge que no és regular és el conjunt de cadenes tal que { anbn | n ≥ 0 }. Intuïtivament es veu que no es pot reconèixer amb un autòmat finit, ja que té una memòria finita i no pot recordar el nombre exacte d'as.[4]

Formalismes equivalents[modifica]

Un llenguatge regular satisfà les següents propietats equivalents:

  1. És el llenguatge d'una expressió regular.
  2. És el llenguatge acceptat per un autòmat finit no determinista.
  3. És el llenguatge acceptat per un autòmat finit determinista.
  4. Es pot generar amb una gramàtica regular.
  5. És el llenguatge acceptat per un autòmat finit alternant.
  6. Es pot generar amb una gramàtica de prefix.
  7. És el llenguatge acceptat per una màquina de Turing de només lectura.
  8. Es pot definir amb lògica de segon ordre.

Propietats de clausura[modifica]

Els llenguatges regulars son tancats segons vàries operacions. Si els llenguatges K i L son regulars, també ho serà el resultat de les operacions següents:

  • El conjunt d'operacions Booleanes: unió K ∩ L, intersecció K ∩ L i complementari L
  • Les operacions regulars K ∪ L, concatenació K ∘ L, i clausura de Kleene L*
  • Operacions trio: homomorfisme de cadenes, la seva inversa i intersecció amb llenguatges regulars. Com a conseqüència, son tancats per operacions amb Transductor d'estats finits, com el quocient K/L amb llenguatges regulars.
  • La inversa LR. Donat un autòmat finit no determinista que reconeix L, es pot obtenir un autòmat per reconèixer LR fent revertint totes les transicions i intercanviant l'estat inicial per l'estat final.

Problemes de decisió[modifica]

Donats dos autòmats finits deterministes A i B, és decidible saber si accepten el mateix llenguatge.[5] Com a conseqüència, usant les propietats de clausura, els següents problemes també son decidibles per qualsevol autòmat finit A i B, que accepten els llenguatges LA i LB respectivament:

  • Inclusió: LA ⊆ LB?
  • Disjunció: LA ∩ LB = {} ?
  • Buit: LA = {} ?
  • Universalitat: LA = Σ* ?
  • Membre: donat a ∈ Σ*, a ∈ LB ?

Per expressions regulars, el problema d'universalitat és NP-complet inclús per un alfabet simple.[6] Per alfabets més grans, el problema és PSPACE-complet.[7][8]

Complexitat[modifica]

En complexitat computacional, la classe de complexitat de tots els llenguatges regulars s'anomena sovint com REGULAR o REG i és equivalent a DSPACE (O (1)), és a dir, el conjunt de problemes de decisió que es poden resoldre en espai constant (l'espai utilitzat és independent de la mida d'entrada).

REGULAR ≠ AC0, ja que conté el problema de paritat de determinar si el nombre de bits a 1 a l'entrada és parell o senar, i aquest problema no està a AC0.

D'altra banda, REGULAR no conté AC0, ja que el llenguatge no regular dels palíndroms, o el llenguatge no regular es poden reconèixer per AC0.[9]

Si un llenguatge es no regular, requereix que una màquina amb almenys espai Ω(log log n) per reconèixer-lo. Dit d'altra manera, la classe DSPACE (o(log log n)) és igual a la classe dels llenguatges regulars.[10]

Posició a la jerarquia de Chomsky[modifica]

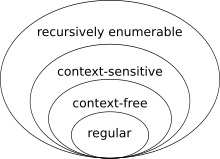
Classes de llenguatges regulars dins la jerarquia de Chomsky

Per trobar la posició dels llenguatges regulars dins de la jerarquia de Chomsky cal notar que tot llenguatge regular és lliure del context. A l'inrevés no és cert: per exemple el llenguatge consistent en totes les cadenes que tenen el mateix nombre d'as i de bs és lliure del context però no és regular. Per provar que un llenguatge d'aquest tipus no és regular es fa servir el teorema de Myhill-Nerode o el Lema de bombament.[11]

Els llenguatges regulars tenen subclasses força importants:

  • Llenguatges finits: aquells llenguatges que contenen només un nombre finit de paraules (no confondre amb un llenguatge generat per un autòmat finit). Aquests llenguatges son regulars, ja que es poden crear amb una expressió regular que és la unió de cada paraula del llenguatge.
  • Llenguatges lliures d'estrella, que es poden descriure amb una expressió regular construïda des del símbol buit, lletres, concatenació i tots els operadors boolens, incloent-hi complement però no la clausura de Kleene. Aquesta classe inclou tots els llenguatges finits.[12]

Referències[modifica]

  1. ↑ The Oxford handbook of computational linguistics. Oxford: Oxford University Press, 2003. ISBN 0198238827. 
  2. ↑ V., Lawson, Mark. Finite automata. Boca Raton: Chapman & Hall/CRC, 2004. ISBN 1584882557. 
  3. ↑ Michael., Sipser,. Introduction to the theory of computation. 3a edició. Boston, MA: Cengage Learning, 2013. ISBN 9781133187790. 
  4. ↑ Samuel., Eilenberg,. Automata, languages, and machines.. Nova York,: Academic Press, 1974-76. ISBN 0122340019. 
  5. ↑ 1939-, Hopcroft, John E.,. Introduction to automata theory, languages, and computation. Reading, Mass.: Addison-Wesley, 1979. ISBN 020102988X. 
  6. ↑ V., Aho, Alfred. The design and analysis of computer algorithms. Reading, Mass.: Addison-Wesley Pub. Co, [1974]. ISBN 0201000296. 
  7. ↑ «MR: Matches for: MR=421145». [Consulta: 13 febrer 2019].
  8. ↑ Bowen Hurt III, Harry On the time and tape complexity of languages, Agost 1973, pàg. 106.
  9. ↑ 1948-, Cook, Stephen,. Logical foundations of proof complexity. Cambridge: Cambridge University Press, 2010. ISBN 9780511677168. 
  10. ↑ Stearns, R. E.; Hartmanis, J.; Lewis, P. M. «Hierarchies of memory limited computations». 6th Annual Symposium on Switching Circuit Theory and Logical Design (SWCT 1965), 1965-10, pàg. 179–190. DOI: 10.1109/FOCS.1965.11.
  11. ↑ «How to prove that a language is not regular?». [Consulta: 13 febrer 2019].
  12. ↑ Logic and automata : history and perspectives. Amsterdam: Amsterdam University Press, 2008. ISBN 9789048501281. 
Obtingut de «https://ca.wikipedia.org/w/index.php?title=Llenguatge_regular&oldid=33388173»