Corba de Watt
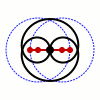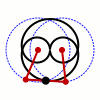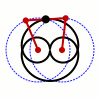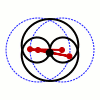
En matemàtiques la corba de Watt és una corba algebraica plana tricircular de grau sis. És generada per dos circumferències de radi b amb distància entre centres 2a (normalment es representen en coordenades cartesianes situant els centres a (±a, 0). Un segment de recta de llargada 2 c connecta un punt de cada una de les circumferències, i el punt mitjà del segment dibuixa la corba de Watt a mesura que giren les circumferències. Va sorgir relacionada amb els treballs de James Watt sobre la màquina de vapor.
L'equació de la corba es pot donar en coordenades polars com
Deducció
[modifica]Coordenades polars
[modifica]L'equació polar per a la corba es pot obtenir de la manera següent:[1] Treballant al pla complex, siguin els centres dels circumferències a a i −a, si el segment que les connecta té els extrems a −a +bei λ i a +be i ρ. Sia ψ l'angle de la inclinació del segment amb el seu punt mitjà a re i θ. Llavors els extrems també venen donats per re i θ ± ce i ψ. Establint la igualtat de les expressions corresponents als mateixos punts s'obté
Add these and divide by two to get
Sumant-les i dividint entre dos dona
Comparant radis i angles dona
De manera similar, restant les dues primeres equacions i dividint el resultat entre 2 dona
Escrivint
Llavors
Coordenades Cartesianes
[modifica]Desenvolupant l'equació polar dona
Fent d ²=a ²+b ²-c ² ho simplifica a
Forma de la corba
[modifica]La construcció requereix un quadrilàter amb costats 2a, b, 2c, b. Qualsevol costat ha de ser menor que la suma dels costats restants, donat que la corba és nul·la (com a mínim al pla real) llevat que a<b +c i c<b +a.
Té un punt de pas per l'origen si existeix un triangle amb costats a, b i c. Donades les condicions prèvies, això significa que la corba talla l'origen si i només si b <a +c. Si b=a+c llavors dues branques de la corba es troben a l'origen amb una tangent vertical comuna, fent-lo un punt de quàdruple.
Donats b <a +c, la forma de la corba està determinada per la magnitud relativa de b i d. Si d és imaginari, és a dir si a²+b²=<c² llavors la corba té la forma de la xifra vuit. Si d és 0 llavors la corba és una xifra vuit i dues branques de la corba tenen una tangent horitzontal comuna a l'origen. Si 0<d<b llavors la corba té dos punts dobles addicionals a ±d i la corba es creua en aquests punts. Si d =b llavors a =c i la corba es descompon a una circumferència de radi b i una hipopede de Booth. Un cas especial d'aquest és a =c, b =√2c que produeix la Lemniscata de Bernoulli. Finalment, si d >b llavors els punts ±d encara són solucions de l'equació cartesiana de la corba, però la corba no creua aquests punts i són acnodes. La corba una altra vegada té forma d'una xifra vuit encara que la forma es distorsiona si d és a la vora de b.
Donats b >a +c, la forma de la corba està determinada per les mides relatives de a i c. Si a <c llavors la corba té la forma de dos bucles que es creuen entre ells a ±d. Si a =c llavors la corba es descompon en una circumferència de radi b i una hipopede de Booth. Si a >c llavors la corba no creua l'eix x i consta de dos ovals aplanats.[2]
El mecanisme de Watt
[modifica]
Quan la corba creua l'origen, l'origen és un punt d'inflexió i per això té contacte de l'ordre 3 amb una tangent. Tanmateix, si a²=b²+<c² llavors té contacte d'ordre 5 amb la tangent, en altres paraules la corba és una aproximació propera d'una recta. Aquesta és la base del mecanisme de Watt.
Referències
[modifica]- Weisstein, Eric W., «Watt's Curve» a MathWorld (en anglès).
- O'Connor, John J.; Robertson, Edmund F. «Watt's Curve» (en anglès). MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland.
- "Courbe de Watt" a Encyclopédie des Formes Mathématiques Remarquables (en francès)
- Catalan, M.E. «Sur la Courbe de Watt». Mathesis, V, 1885, pàg. 154.
- Rutter, John W. Geometry of Curves. CRC Press, 2000, p. 73ff.. ISBN 1584881666.

![{\displaystyle r^{2}=b^{2}-\left[a\sin \theta \pm {\sqrt {c^{2}-a^{2}\cos ^{2}\theta }}\right]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd6e3921b0bd544992632a8d945be2a2e9dea8d2)









![{\displaystyle r^{2}=b^{2}\cos ^{2}\alpha =b^{2}-b^{2}\sin ^{2}\alpha =b^{2}-\left[a\sin \theta \pm {\sqrt {c^{2}-a^{2}\cos ^{2}\theta }}\right]^{2}.,\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d3b488696dbd57628e3076b0d5f652a63af8eaf)





