Difusió

un procés de difusió de la ciència. Algunes partícules es dissolen en un got d'aigua. Inicialment, les partícules estan prop d'una cantonada del vidre. Si les partícules de tot aleatòriament es mouen ("difusa") per l'aigua, llavors les partícules eventualment es trobaran distribuïdes aleatòriament i de manera uniforme, i organitzada (però encara la difusió se seguirà produint, només que no hi haurà flux net).

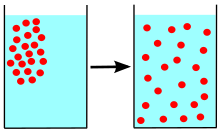
La difusió és un dels diversos fenòmens de transport que es troben a la natura. Una de les característiques distintives és que és el resultat de barrejar o transportar massa sense la necessitat d'un moviment a l'engròs. Per tant, la difusió no s'ha de confondre amb la convecció o advecció, que són altres mecanismes de transport que utilitzen el moviment per moure les partícules d'un lloc a un altre. En llatí "diffundere" significa cap a fora.

Hi ha dues maneres d'introduir el concepte difusió: Una aproximació a partir de les lleis de Fick i la seva conseqüència matemàtica o des del punt de vista Físic, considerant un camí a l'atzar de les partícules que es mouen.

D'acord amb la llei de Fick el flux de difusió és proporcional al gradient de concentracions. El moviment és des de regions de major concentració a menys concentració. Des del punt de vista atomista, la difusió es considera com el moviment aleatori de les partícules difusores. En la difusió molecular, les molècules que es mouen són autopropulsades per energia tèrmica. Aquest passeig aleatori va ser descobert el 1827 per Robert Brown. Ara bé, el concepte de difusió és àmpliament utilitzat en la ciència: la física (difusió de partícules), la química i la biologia, la sociologia, l'economia i les finances (difusió de la gent, les idees i dels valors de preus). Pel que sembla, sempre el concepte del moviment a l'atzar en els conjunts d'individus és aplicable.

Models Bàsics de Difusió

Flux de difusió

Cada model de difusió expressa el flux de difusió a través de concentracions, densitats o derivats. Flux és el vector $\mathbf {J}$., la transferència d'una quantitat física $N$ a través d'una àrea petita $\Delta S$, amb la normal $\nu$ i el temps $\Delta t$ és:

$\Delta N=(\mathbf {J} ,\nu )\Delta S\Delta t+o(\Delta S\Delta t)\,$

On $(\mathbf {J} ,\nu )$ és el producte interior i $o(...)$ és una notació. Si es fa servir la notació del vector àrea $\Delta \mathbf {S} =\nu \Delta S$ aleshores:

$\Delta N=(\mathbf {J} ,\Delta \mathbf {S} )\Delta t+o(\Delta \mathbf {S} \Delta t)\,.$

La dimensió del flux de difusió és [flux] = [quantitat] / ([temps] • [àrea]). La quantitat física difusora $N$ pot ser el nombre de partícules, la massa, energia, càrrega elèctrica, o qualsevol altra quantitat escalar extensa. Per la seva densitat, l'equació de difusió té la forma:

${\frac {\partial n}{\partial t}}=-\nabla \cdot \mathbf {J} +W\,$

On $W$ és la intensitat de qualsevol font local, com per exemple la velocitat d'una reacció química. Per l'equació de difusió, en les condicions límits del no-flux, es pot formular $(\mathbf {J} (x),\nu (x))=0$ en el límit, on $\nu$ és la normal del punt $x$ al límit.

Llei de Fick i equacions

• 1a llei de Fick: el flux de difusió és proporcional al gradient negatiu de la concentració:

$\mathbf {J} =-D\nabla n\,\;\;J_{i}=-D{\frac {\partial n}{\partial x_{i}}}\ .$

Col·lisions aleatòries de les partícules en un gas.

D és el coeficient de difusió, considerem dos gasos amb molècules del mateix diàmetre d i la massa m (autodifusió). En aquest cas, la teoria elemental significa camí lliure mitjà de difusió per al coeficient de difusió:

$D={\frac {1}{3}}\ell v_{T}={\frac {2}{3}}{\sqrt {\frac {k_{\rm {B}}^{3}}{\pi ^{3}m}}}{\frac {T^{3/2}}{Pd^{2}}}\,$

On k_B és la constant de Bolzmann T la temperatura, P la pressió, $\ell$ és el camí lliure mitjà i v_T és la velocitat tèrmica mitjana.

$\ell ={\frac {k_{\rm {B}}T}{{\sqrt {2}}\pi d^{2}P}}\,,\;\;\;v_{T}={\sqrt {\frac {8k_{\rm {B}}T}{\pi m}}}\,.$

Podem veure que el coeficient de difusió en l'aproximació recorregut lliure mitjà creix amb T com T^3/2 i disminueix amb P com 1/P. Si s'utilitza per P la llei del gas ideal P=RnT amb la concentració total de n, llavors es pot veure que per a la concentració de n donat el coeficient de difusió creix amb T com T^3/2 i per la temperatura donada, disminueix amb la concentració total com 1/n.

Donat dos gasos diferents, A i B, amb masses moleculars m_A, m_B i diàmetres moleculars d_A, d_B, l'estimació camí lliure mitjà del coeficient de difusió de A a B i B a A és:

$D_{\rm {AB}}={\frac {1}{3}}{\sqrt {\frac {k_{\rm {B}}^{3}}{\pi ^{3}}}}{\sqrt {{\frac {1}{2m_{\rm {A}}}}+{\frac {1}{2m_{\rm {B}}}}}}{\frac {4T^{3/2}}{P(d_{\rm {A}}+d_{\rm {B}})^{2}}}\,$

• La corresponent equació de difusió, 2a llei de Fick és:

${\frac {\partial n(x,t)}{\partial t}}=\nabla \cdot (D\nabla n(x,t))=D\Delta n(x,t)\,$

On $\Delta$, és l'operador de Laplace:

$\Delta n(x,t)=\sum _{i}{\frac {\partial ^{2}n(x,t)}{\partial x_{i}^{2}}}\ .$

Equació d'Onsager per difusió i termodifusió de multicomponents

Les lleis de Fick de la difusió descriuen una barreja en un medi. La concentració d'aquesta barreja ha de ser petita i el seu gradient també. la força motriu en la difusió en la primera llei de Fick és l'antigradient de la concentració $-\nabla n$.

El 1931, Lars Onsager va incloure el procés de transport de multi omponents en el context general per equilibris no lineals de la termodinàmica. Per al transport de multicomponents,

$\mathbf {J} _{i}=\sum _{j}L_{ij}X_{j}\,$

On $\mathbf {J} _{i}$ és el flux de la quantitat física i (component) i $X_{j}$ és la força termodinàmica j. Les forces termodinàmiques dels processos de transport van ser introduïdes per Onsager com el gradient espacial dels derivats de la densitat d'entropia:

$X_{i}={\rm {grad}}{\frac {\partial s(n)}{\partial n_{i}}}\,$

On $n_{i}$ són les "les coordinades termodinàmiques". Per la transferència de calor i massa es pot prendre $n_{0}=u$ (la densitat d'energia interna) i $n_{i}$ és la concentració per la component i. Les forces impulsores són els corresponents vectors espacials.

$X_{0}={\rm {grad}}{\frac {1}{T}}\,\;\;\;X_{i}=-{\rm {grad}}{\frac {\mu _{i}}{T}}\;(i>0),$

Perquè

${\rm {d}}s={\frac {1}{T}}{\rm {d}}u-\sum _{i\geq 1}{\frac {\mu _{i}}{T}}{\rm {d}}n_{i}$

On T és la temperatura absoluta i $\mu _{i}$ és el potencial químic del component i. Cal destacar que les equacions de difusió separades descriuen el transport de la mescla i la massa sense moviment a granel. Per tant, es poden menysprear els termes amb variació de la pressió total. És possible per la difusió de petits additius i petits gradients.

Vegeu també

• Moviment brownià