Distància focal
En òptica, la distància focal (concretament la distància focal frontal, diferent de la distància focal de brida) és la distància entre el centre òptic d'una lent i el punt on la imatge és projectada, o bé la distància entre el centre òptic i el punt on convergeixen les prolongacions dels raigs de llum, si es tracta d'una lent divergent. Per a lents simples, aquest és un paràmetre intrínsec, puix que és propi de cada lent i no és modificable.
La distància focal d'una lent varia amb la longitud d'ona de la llum que la travessa. Això dona lloc a l'aberració cromàtica. En la construcció d'objectius, aquesta aberració es corregeix combinant dues o més lents, cada una de les quals anul·len o redueix l'aberració cromàtica de les altres.
En fotografia, com més llarga sigui la distància focal, una petita potència òptica, es tindrà més capacitat d'augmentar la mida d'objectes distants, tindrem un angle de visió petit. D'altra banda, si tenim una distància focal curta, una gran potència òptica, tindrem un gran angle de visió.
La distància focal d'una lent també varia la profunditat de camp: quanta més distància focal tingui la lent, menys profunditat de camp tindrà i es podran apreciar més elements desenfocats. D'altra banda, quanta menys distància focal tingui la lent, més profunditat de camp tindrà i, conseqüentment, es podran apreciar més elements enfocats.
Aproximació de lents primes[modifica]
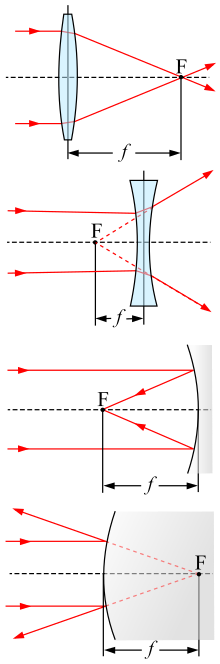
Per a una lent prima a l'aire, la distància focal és la distància des del centre de la lent fins als principals focus (o punts focals) de la lent. Per una lent convergent (per exemple, una lent convexa), la longitud focal és positiva, i és la distància a la qual s'enfocarà un feix de llum col·limada a un sol punt. Per una lent divergent (per exemple, una lent còncava), la longitud focal és negativa, i és la distància fins al punt sobre el qual apareix un feix col·limat per a ser divergit després de passar a través de la lent.
Quan s'usa una lent per formar una imatge d'un objecte, la distància de l'objecte a la lent o, la distància de la lent a la imatge v, i la longitud focal f estan relacionats per
.
La longitud focal d'una lent prima es pot mesurar fàcilment mitjançant l'ús de la lent per formar una imatge d'una font de llum distant en una pantalla. La lent és moguda fins que una imatge nítida es forma sobre la pantalla. En aquest cas 1/u és menyspreable, i la longitud focal llavors ve donada per:
.
Sistemes òptics generals[modifica]
Per a lents gruixudes (que tinguin un gruix no menyspreable), o un sistema d'imatge que consta de diverses lents i / o miralls (per exemple, una lent fotogràfica o un telescopi), la longitud focal sovint es diu la distància focal efectiva (EFL), per distingir-lo d'altres paràmetres utilitzats comunament:

- Longitud focal frontal (FFL) o la distància focal frontal (FFD) (SF) és la distància des del punt focal frontal del sistema (F) fins al vèrtex de la primera superfície òptica (S1).[1][2]
- Longitud focal de darrere (BFL) o la distància focal posterior (BFD) (s'F ') és la distància des del vèrtex de l'última superfície òptica del sistema (S2) fins al punt focal posterior (F').[1] [2]
Per a un sistema òptic en l'aire, la longitud focal efectiva (F i F ') dona la distància de davant i darrere dels plans principals (H i H') fins als centres de coordinació corresponents (F i F '). Si el medi circumdant no és aire, llavors la distància es multiplica per l'índex de refracció del medi (n és l'índex de refracció de la substància de la qual està feta la lent en si; n1 és l'índex de refracció de qualsevol mitjà al davant de la lent ; n2 és el de qualsevol tipus de suport a la part posterior de la mateixa). Alguns autors anomenen aquestes distàncies els distàncies focals davanteres / posteriors, distingint-les de les distàncies focals davanteres / posteriors que s'han definit anteriorment. [1]
En general, la longitud focal o EFL és el valor que descriu la capacitat del sistema òptic per enfocar la llum, i és el valor que s'utilitza per calcular l'ampliació del sistema. Els altres paràmetres s'utilitzen en la determinació en la qual es formarà una imatge d'una posició d'objecte donada.
Per al cas d'una lent de gruix d en l'aire (n1 = n2 = 1), i superfícies amb radis de curvatura R1 i R2, la distància focal efectiva f es dona per l'equació del fabricant de lents:
,
on n és l'índex de refracció del medi de la lent. La quantitat 1/f també es coneix com la potència òptica de la lent.
La distància focal frontal corresponent és:[3]
,
i la distància focal posterior:
.
En la convenció de signes utilitzada aquí, el valor de R1 serà positiu si la primera superfície de la lent és convexa, i negatiu si és còncava. El valor de R2 és negatiu si la segona superfície és convexa i positiva si còncava. Recordeu que les convencions de signes varien entre els diferents autors, la qual cosa resulta en diferents formes d'aquestes equacions en funció de la convenció utilitzada.
Per a un mirall esfèric corbat en l'aire, la magnitud de la distància focal és igual al radi de curvatura del mirall dividit per dos. La distància focal és positiva per a un mirall còncau, i negatiu per a un mirall convex. A la convenció de signes utilitzats en el disseny òptic, un mirall còncau té un radi de curvatura negatiu, així
,
on R és el radi de curvatura de la superfície del mirall.
En fotografia[modifica]
Les longituds focals de la lent de la càmera solen especificar-se en mil·límetres (28mm, 35mm, 50mm,etc.), però algunes lents més antigues estan marcades en centímetres (cm) o polzades.
La longitud focal (f) i el camp de visió (FOV) d'una lent són inversament proporcionals. Per a una lent rectilínia estàndard, FOV = 2 arctan x / 2f, on x és la diagonal de la pel·lícula.
Quan una lent fotogràfica està en "infinit", el seu punt nodal posterior està separat del sensor o la pel·lícula, al pla focal, per la distància focal de la lent. Els objectes llunyans de la càmera produeixen imatges nítides al sensor o la pel·lícula, que també es troben al pla d'imatges.
Per fer que els objectes més propers estiguin enfocats, s'ha d'ajustar la lent per augmentar la distància entre el punt nodal posterior i la pel·lícula, per col·locar la pel·lícula al plànol de la imatge. La distància focal (f), la distància del punt nodal frontal a l'objecte a fotografiar (s1), i la distància des del punt nodal posterior fins al pla d'imatge (s2) es relacionen a continuació per:
A mesura que s1 disminueix, s2 s'ha d'augmentar. Per exemple, considerem una lent normal per a una càmera de 35 mm amb una distància focal de f = 50 mm. Per centrar un objecte llunyà (s1 ≈ ∞), el punt nodal posterior de la lent ha d'estar situat a una distància s2 = 50 mm del pla d'imatge. Per centrar un objecte a 1 m de distància (s1 = 1,000 mm), la lent s'ha de moure a 2,6 mm més lluny del pla d'imatge, a s2 = 52,6 mm.
La distància focal d'una lent determina l'ampliació a la qual s'alcen els objectes distants. És igual a la distància entre el pla d'imatge i un forat que les imatges distants objecten la mateixa mida que la lent en qüestió. Per a les lents rectilínies (és a dir, sense distorsió d'imatge), la imatge d'objectes distants està ben modelada com a model de càmera de forat. [4] Aquest model condueix al model geomètric simple que utilitzen els fotògrafs per computar l'angle de visió d'una càmera; en aquest cas, l'angle de visió depèn només de la proporció de la distància focal a la mida del film. En general, l'angle de visió depèn també de la distorsió.
Una lent amb una distància focal equivalent a la mida diagonal del film o el format del sensor es coneix com una lent normal; el seu angle de visió és similar a l'angle subtendit per una impressió prou gran vista a una distància de visió típica de la diagonal d'impressió, que per tant dona una perspectiva normal en veure la impressió; aquest angle de vista és d'uns 53 graus en diagonal. Per a càmeres de format complet de 35 mm, la diagonal és de 43 mm i una lent típica "normal" té una distància focal de 50 mm. Una lent amb una distància focal més curta que la normal es refereix sovint com un angular (típicament de 35 mm i menys, per a càmeres de format de 35 mm), mentre que una lent significativament més llarga que la normal es pot anomenar teleobjectiu (normalment de 85 mm i més, per a càmeres de format de 35 mm). Tècnicament, les lents de llarga distància focal són només "teleobjectiu" si la longitud focal és més llarga que la longitud física de la lent, però el terme s'utilitza sovint per descriure qualsevol lent de focal llarg.
A causa de la popularitat de l'estàndard de 35 mm, les combinacions de lent-càmera es descriuen sovint en termes de la seva distància focal equivalent a 35 mm, és a dir, la distància focal d'una lent que tindria el mateix angle de visió o camp de visió, si s'utilitza en una càmera full-frame de 35 mm. L'ús d'una distància focal equivalent a 35 mm és particularment comú amb les càmeres digitals, que sovint utilitzen sensors de menys de 35 mm de pel·lícula, per la qual cosa requereixen longituds focals corresponents per aconseguir un angle de visió determinat, per un factor conegut com el factor de collita.
Referències[modifica]
- ↑ 1,0 1,1 Greivenkamp, John E. Field Guide to Geometrical Optics. SPIE Press, 2004, pp. 6--9. ISBN 978-0-8194-5294-8..
- ↑ 2,0 2,1 Hecht, Eugene. Optics (en anglès). (4th ed.). Addison Wesley, p. 168. ISBN 978-0805385663.
- ↑ Hecht, Eugene. Optics (en anglès). 4a. Addison Wesley, p. 168. ISBN 978-0805385663..
Vegeu també[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Distància focal |







