Epicicloide
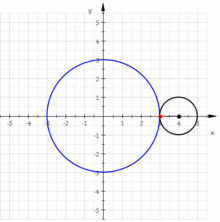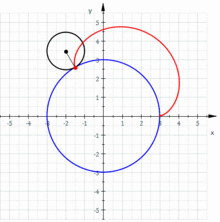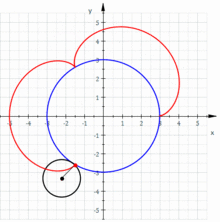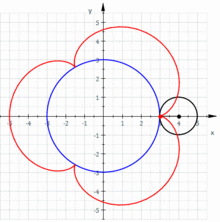
Una epicicloide és la corba generada per un punt d'un cercle que gira sense lliscar sobre un altre cercle. Per tant, és un tipus particular d'epitrocoide (quan el punt associat resulta estar sobre el cercle generador).
Les seves equacions paramètriques són:
on R és el radi del cercle fix i r el radi del cercle generador. Si definim q = R/r, aquest sistema es pot escriure com:
La corba està formada per arcs isomètrics separats per vèrtexs. Si q és racional, el numerador representa el nombre d'arcs de la corba. El cas particular en què q = 1 (és a dir, els radis dels dos cercles són iguals) la corba resultant s'anomena cardioide; el cas en què q = 2 (el cercle fix és el doble del generador) la corba s'anomena nefroide.
La corba apareix per primera vegada a l'Antiguitat: Aristòtil i després Claudi Ptolemeu l'utilitzen per descriure el moviment dels planetes dins del model geocèntric. El 1674 Olaus Rømer, estudiant rodes amb engranatges, redescobreix l'epicicloide i li dona el seu nom actual i demostra que si les dents d'un engranatge es fan en forma de segments d'epicicloide el fregament entre les dents és mínim.
Vegeu també[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Epicicloide |



![{\displaystyle x(\theta )=r\left[(q+1)\cos \theta -\cos(q+1)\theta \right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3aa8202ea51e739a14786e7327a9b368d207ee2)
![{\displaystyle y(\theta )=r\left[(q+1)\sin \theta -\sin(q+1)\theta \right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb9b8596c4130cb1fcb9b504716f06fbe03d2b19)