Equacions de Lotka-Volterra

Model de fases de les equacions de Lotk-Volterra.

Les equacions de Lotka-Volterra, o també conegudes com equacions de depredador-presa, són unes equacions diferencials de primer ordre que modelen l'evolució ecològica de dues poblacions d'animals: depredadors (llops) i preses (conills). Amb aquest model s'intenta explicar com funciona la coexistència de dues espècies. Aquest model va ser desenvolupat per Alfred J. Lotka al 1925 i Vito Volterra al 1926.

El model

Les poblacions de depredadors $H(t)$ i preses $P(t)$ satisfan el sistema d'equacions diferencial

$\left\{{\begin{matrix}{\frac {dH}{dt}}&=&H(a-\alpha P)\\{\frac {dP}{dt}}&=&P(-c+\gamma H)\end{matrix}}\right.$

amb $a,c,\alpha$ i $\gamma$ sent constants positives del sistema.

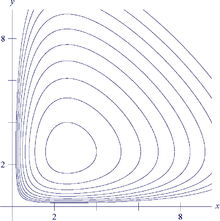
Si $a=c$ i $\alpha =\gamma$ llavors una propietat fonamental d'aquestes equacions és que es preserva la quantitat total de depredadors i preses: ${\frac {d}{dt}}(H(t)+P(t))=0.$ En aquest cas, el sistema és hamiltonià.

Bibliografia

• Boyce, Wylliam E.; Diprima, Richard C. Ecuaciones diferenciales y problemas con valores en la frontera (en castellà). 3a. Balderas 95, México, D.F.: Editorial Limusa, S.A. de C.V. Grupo Noriega Editores, 1996, p. 744. ISBN 968-18-0107-05.