Graf dual

El graf G és dual del G ', i viceversa.

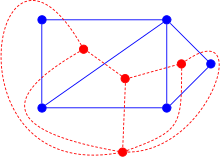
A teoria de grafs, un ' graf dual G d'un graf planar G és un graf que té un vèrtex per cada regió de G , i una aresta per cada aresta en G unint a dues regions veïnes.

Propietats

G ' i G "són duals de G , però no isomorfs.

• Si G ' és el graf dual d'un graf planar G , llavors G' també és un graf planar (que pot tenir bucles i arestes múltiples).
• Si G ' és el graf dual d'un graf planar G , llavors el graf dual de G' és G .
• Si G és un graf planar, llavors pot ser que no existeixi un únic graf dual per G , en el sentit que G pot tenir grafs duals no-isomorfs, depenent de la distribució particular dels plans. A la figura, G 'i G "no són isomorfs perquè G' té un node amb grau 6 (la regió exterior) que G" no té (veure diagrama).

Graf autodual

Un graf autodual és aquell que és isomorf al seu dual.

Propietats

Siguin dos grafs planars G = (V, E) i G '= (V', E ') , els conjunts de regions són R i R' , respectivament, aleshores:

• |E '|=|E|
• |V '|=|R|
• |R '|=|V|

Referències

• H. Whitney, Non-separable and planar gràfics , Trans. Amer. Math. Soc 34 (1932), 339-362.