Teoria de grafs

La teoria de grafs és una branca de les matemàtiques i la informàtica que es dedica a l'estudi dels grafs, estructures matemàtiques utilitzades per a modelitzar relacions entre parelles d'objectes. En aquest context, un graf consisteix en una col·lecció de vèrtexs o nodes connectats per línies anomenades arestes. Els grafs poden ser no dirigits, és a dir sense fer distinció entre els dos vèrtexs associats a cada aresta, o dirigits, les arestes dels quals van d'un vèrtex a un altre; en aquest cas, les arestes s'anomenen arcs. Els grafs se solen representar gràficament amb un punt o cercle per cada vèrtex, i una línia entre vèrtexs connectats. Si el graf és dirigit, els arcs se simbolitzen amb fletxes, indicant la direcció de la relació entre els dos vèrtexs.

Els grafs són un dels principals objectes d'estudi de la matemàtica discreta. Les aplicacions de la teoria de grafs giren al voltant d'estructures que poden ser sistematitzades amb grafs, com per exemple l'estructura de llocs web, l'anàlisi de xarxes, l'estudi de molècules en química i física, o altres camps com els estudis sociològics.

El primer problema conegut de la teoria de grafs és el problema dels set ponts de Königsberg. Fou plantejat per Leonhard Euler el 1736 .

Definicions

Article principal: Graf (matemàtiques)

Xarxa és un conjut d'elements o nodes units per enllaços físics. Un graf és un objecte matemàtic que permet modelar una xarxa.

En el sentit més habitual del terme, un graf simple és un parell ordenat G = (V, E), format per un conjunt finit no buit V de vèrtexs o nodes o punts juntament amb un conjunt finit E d'arestes o arcs, que són subconjunts de 2 elements de V (és a dir, una aresta relaciona dos vèrtexs, i aquesta relació es representa mitjançant un parell no ordenat dels vèrtexs respecte de l'aresta en qüestió).

Altres definicions de graf parteixen de diferents concepcions del conjunt d'arestes. En un sentit més general, V és un conjunt amb una relació d'incidència que associa dos vèrtexs amb cada aresta. En un altre sentit, E és un multiconjunt de parells no ordenats de vèrtexs (no necessàriament diferents).

Multigraf és un graf que conté parells de vèrtexs units per més d'una aresta. Observem que els vèrtexs Q i S estan units per 2 arestes i els vèrtexs T i S per 3 arestes.

Multigraf

Un llaç o bucle és una aresta que uneix un vèrtex amb ell mateix,

Pseudograf és un multigraf amb llaços.

Pseudograf

Graf dirigit o dígraf és un graf amb els enllaços o arestes, que ara es diran arcs, que van en una única direcció. Un arc és, en aquest cas, un parell ordenat de vèrtexs.

Graf dirigit o dígraf

Un recorregut en un graf és una manera d'assolir un vèrtex des d'un altre recorrent un conjunt d'arestes una darrera l'altra.

Graf dirigit

Per exemple, P $\longrightarrow$ Q$\longrightarrow$ R és un recorregut per anar del vèrtex P a l'R. Aquest recorregut té longitud 2.

P $\longrightarrow$ S$\longrightarrow$ Q $\longrightarrow$ R$\longrightarrow$ S $\longrightarrow$T és un recorregut per anar del vèrtex P al T. Aquest recorregut té longitud 5.

Un recorregut en el qual els vèrtexs apareixen una sola vegada s'anomena cami.

P $\longrightarrow$ Q$\longrightarrow$ R$\longrightarrow$ S és un camí per anar de P a S.

Hom diu que els vèrtexs que pertanyen a una aresta són els extrems o vèrtexs finals de l'aresta. Pot donar-se el cas que un vèrtex pertanyi al graf i que no pertanyi a cap aresta.

Habitualment, V i E són conjunts finits, i molts dels resultats coneguts no són certs (o són diferents) per a grafs infinits, perquè molts dels arguments fallen en el cas infinit. L'ordre d'un graf és |V|, el nombre dels seus vèrtexs. La grandària o mida d'un graf és |E|, el nombre de les seves arestes. El grau o valència d'un vèrtex és el nombre d'arestes que estan connectades amb el vèrtex, amb la convenció que una aresta que connecta un vèrtex amb ell mateix (un bucle o llaç) es compta dos cops. El grau d'un vèrtex es simbolitza amb la lletra d. d(número de vèrtex)=número d'arestes que hi conflueixen.

Per a una aresta {x, y}, hom acostuma a emprar la notació més breu xy.

Representació d'un graf amb 6 vèrtexs i 7 arestes

Exemple

V=conjunt de vèrtexs= {1,2,3,4,5,6}

E=conjunt d'arestes= {(6,4),(4,5),(5,1),(1,2),(2,3),(3,4),(5,2)}

L'ordre de G és el número de vèrtexs que té. n=|V|= ordre de G. En la figura tenim n=6.

La mida de G és el número d'arestes que té. m=|E|=mida de G. En la figura tenim m=7.

El graf de la figura té ordre 6 i mida 7.

El vèrtex 4 té grau 3. És a dir, d(4)=3

Seqüència de graus: 2,3,2,3,3,1

Graus de cada vèrtex d(1)=2, d(2)=3, d(3)=2, d(4)=3, d(5)=3, d(6)=1

En tot graf, la suma dels graus de tots els vèrtexs és el doble del nombre d'arestes. $\sum$ d(v)=2m.

Dos vèrtexs són adajcents si hi ha una aresta que els uneix. Per exemple, els vèrtexs 4 i 5 són adjacents.

Exemple

El joc del dodecaedre(Hamilton, 1859) és un exemple de graf. Es tracta de trobar un camí que passi per cada ciutat(vèrtexs) una única vegada.

E(G1

Camí de Hamilton en 3D

Camí de Hamilton

Connexió

Podem combianr 2 grafs per fer un graf més gran. Si els dos grafs són G₁=(V(G₁), E(G₁)) i G₂=(V(G₂), E(G₂)) són disjunts aleshores la seva unió G₁$\cup$G2 és el graf amb vèrtexs V(G₁)$\cup$ V(G₂) i la família d'arestes E(G₁) $\cup$ E(G₂).

Graf connex

És un graf que no es pot expressar com la unió de dos grafs.

I és no connex en cas contrari.

Cada graf no connex G es pot expressar com la unió de grafs connexos, cadascun dels quals s'anomena component de G.

Exemple

El graf G és no connex amb tres components

Graf no connex amb tres components connexes

Representació

Representacions d'un graf

Encara que és convenient representar un graf per un diagrama de punts units per línies, aquesta representació pot ser inadequada si volem emmagatzemar un graf gran en un ordinador. Podem epresentar un graf amb una llista o amb una matriu.

1.- Amb una llista

Una manera de representar un graf simple és utilitzant una llista dels vèrtexs adjacents a cada vèrtex.

Observem el graf següent:

Graf amb els vèrtexs etiquetats

u: v,y v: u,w,y w: v,x,y x: w,y y: u,v,w,x

Hem construït una llista.

2.-Amb matrius

Si G és un graf etiquetat {1,2,3,.....n}, la seva matriu d'adjacència A, és la matriu que té com entrada ij el número d'arestes que uneixen el vèrtex i amb el vèrtex j.

En l'exemple següent n=4 (4 vèrtexs).

Graf etiquetat

A=${\begin{pmatrix}0&1&0&1\\1&0&1&2\\0&1&0&1\\1&2&1&0\\\end{pmatrix}}$

Si a més, les arestes estan etiquetades {1,2,3,.....m}, la matriu d'incidència M és la matriu nxm que té un 1 a la posició ij si el vèrtex i és incident amb l'aresta j i 0 altrament.

La primera fila de la matriu és: 1 perquè el vèrtex 1 és incident amb l'aresta 1, 0 perquè el vèrtex 1 no és incident amb l'aresta 2, 0 perquè el vèrtex 1 no és incident amb l'aresta 3, 1 perquè el vèrtex 1 és incident amb l'aresta 4, 0 perquè el vèrtex 1 no és incident amb l'aresta 5, 0 perquè el vèrtex 1 no és incident amb l'aresta 6. I anàlogament les altres files.

M=${\begin{pmatrix}1&0&0&1&0&0\\1&1&0&0&1&1\\0&1&1&0&0&0\\0&0&1&1&1&1\\\end{pmatrix}}$

Aplicacions

Molécula d'aigua

Molècula d'aspirina

Graf en xarxa format pels editors de Wikipedia (arestes) que contribueixen a versions en diferents idiomes (vèrtexs) durant un mes de l'estiu de 2013

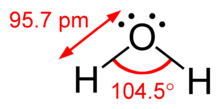
Els grafs es poden usar per modelar diferents tipus de relacions i processos en sistemes físics, biològics, socials i d'informació. Molts problemes pràctics es poden representar mitjançant grafs. les molècules d'aigua i d'aspirina, per exemple es poden representar amb un graf.

A partir de mitjans del segle xx, l'aparició dels ordinadors i el desenvolupament de les telecomunicacions donen un gran impuls a la teoria de grafs.

En ciències de la computació, els grafs s'utilitzen per representar xarxes de comunicació, organització de dades, dispositius computacionals, flux de computació, etc. Per exemple, l'estructura d'enllaços d'un lloc web es pot representar mitjançant un graf dirigit, on els vèrtexs representen les pàgines web, i les arestes dirigides representen enllaços d'una pàgina a una altra. Una aproximació similar pot servir per modelar problemes de viatges, biologia, disseny de xips, i altres camps. El desenvolupament d'algoritmes per tractar grafs és, per tant, d'una gran importància en ciències de la computació. La transformació de grafs s'acostuma a formalitzar mitjançant sistemes de reescriptura de grafs. Altres aplicacions són les bases de dades orientades a grafs, amb l'objectiu d'emmagatzemar les dades d'una forma transaccional i persistent, així com consultar les dades emmagatzemades en forma de graf.

Els mètodes de la teoria de grafs, en diverses formes, són particularment útils en lingüística, ja que el llenguatge natural té sovint una estructura discreta. Tradicionalment, la sintaxi i la semàntica composicional segueixen estructures basades en arbres, el poder expressiu de les quals rau en el principi de composicionalitat, que es modela mitjançant un graf jeràrquic. Algunes aproximacions més contemporànies, com la gramàtica sintagmàtica nuclear, modelen la sintaxi del llenguatge natural utilitzant estructures de trets, que són grafs acíclics dirigits. En semàtica lexical, especialment aplicada als computadors, és més senzill modelar el significat de les paraules quan s'entén cada paraula en termes d'altres paraules relacionades; les xarxes semàntiques són importants, en conseqüència, en lingüística computacional. També són comuns altres mètodes en fonologia (per exemple, la teoria de l'optimalitat, que utilitza grafs de reticle) i morfologia (per exemple, morfologia d'estats finits, que utilitza transductors d'estats finits) en l'anàlisi del llenguatge mitjançant grafs. De fet, l'aplicació dels grafs a la lingüística ha donat lloc a organitzacions com TextGraphs, WordNet o VerbNet, entre altres.

La teoria de grafs també s'utilitza per estudiar molècules en química i física. En física de la matèria condensada, l'estructura tridimensional de simulacions d'estructures atòmiques complicades es pot estudiar quantitativament recopilant estadístiques sobre algunes propietats de la teoria de grafs relacionades amb la topologia dels àtoms. En química, un graf resulta ser un model natural d'una molècula, on els vèrtexs representen els àtoms i les arestes representen els enllaços químics. Aquesta aproximació és ben utilitzada en el processament per ordinador d'estructures moleculars, des d'editors químics a cerques en bases de dades. En física estadística, els grafs poden representar les connexions locals entre parts d'un sistema que interactuen entre elles, així com la dinàmica d'un procés físic en un tal sistema. De la mateixa manera, en neurociència computacional, es poden utilitzar grafs per representar les onnexions funcionals entre les àrees del cervell que interactuen per donar lloc a diversos processos cognitius, on els vèrtexs representen les diferents àrees del cervell, i les arestes representen les connexions entre aquestes àrees. Els grafs també es poden utilitzar per representar els canals a microescala dels mitjans porosos, on els vèrtexs representen els porus, i les arestes representen els petits canals que connecten els porus.

La teoria de grafs s'usa també àmpliament en sociologia, com una manera, per exemple, de mesurar el prestigi d'un actor, o per explorar l'expansió d'un rumor en les xarxes socials, sobretot en programari per a l'anàlisi de xarxes socials. Sota el paraigua de les xarxes socials existeixen diferents tipus de grafs. Els grafs de relacions personals i d'amistat descriuen si les persones es coneixen les unes a les altres. Els grafs d'influència modelen si certes persones poden influir el comportament d'unes altres. Finalment, els grafs de col·laboració modelen si dues persones treballen juntes d'una certa manera, com actuar junts en una pel·lícula.

De la mateixa manera, la teoria de grafs és útil en biologia i els esforços de conservació, on un vèrtex pot representar regions on existeix una certa espècie, i les arestes representen els camins de migració, o els moviments entre regions. Aquesta informació és important quan s'observen els patrons d'alimenació o quan s'analitza la propagació d'una malaltia, de paràsits, o com els canvis de moviment poden afectar altres espècies.

En matemàtiques, els grafs són útils en geometria i en certes àrees de la topologia, com la teoria de nusos. La teoria algebraica de grafs té relació amb la teoria de grups.

Una estructura de graf es pot ampliar assignant un pes (o valor) a cada aresta del graf. Un graf amb pesos, o graf ponderat, es pot utilitzar per representar estructures on les connexions tenen algun valor numèric. Per exemple, si un graf representa una xarxa de carreteres, els pesos podrien representar la longitud de cada carretera.

Història

El problema dels ponts de Königsberg

Es considera que la primera publicació de la història sobre teoria de grafs fou escrita per Leonhard Euler el 1736, Els set ponts de Königsberg. Aquesta publicació, juntament amb la publicació de Vandermonde sobre el Problema de la ruta del cavall, va portar a l'analysis situs iniciat per Leibniz. La fórmula d'Euler que relaciona el nombre d'arestes, vèrtexs i cares d'un políedre convex fou estudiada i generalitzada per Cauchy i L'Huilier, i marca l'origen de la topologia.

Més d'un segle després de la publicació d'Euler sobre els ponts de Königsberg i mentre Listing introduïa la noció de topologia, Cayley estava interessat en l'estudi de certes formes analítiques sorgides del càlcul diferencial per tal d'estudiar una classe particular de grafs, els arbres. Aquest estudi tingué moltes implicacions en química teòrica. Les tècniques que s'hi feien servir tenien a veure amb l'enumeració de grafs amb certes propietats. La teoria enumerativa de grafs sorgí a partir dels resultats publicats per Pólya entre 1935 i 1937 i la seva generalització de De Bruijn el 1959. Cayley va relacionar els seus resultats sobre arbres amb els edtudis contemporanis de composició química. La fusió de les idees provinents de les matemàtiques amb les de la química va originar part de la terminologia estàndard de la teoria de grafs.

En particular, Sylvester va introduir el terme "graf" en un estudi publicat el 1878 a la revista Nature, on dibuixava una analogia entre "invariants quàntics" i "covariants"

Graf que representa els ponts de Königsberg

de l'àlgebra i els diagrames moleculars:

«	(anglès) […] Every invariant and co-variant thus becomes expressible by a graph precisely identical with a Kekuléan diagram or chemicograph. […] I give a rule for the geometrical multiplication of graphs, i.e. for constructing a graph to the product of in- or co-variants whose separate graphs are given. […]	(català) […] Qualsevol invariant i covariant es pot, doncs, expressar com un graf idèntic a un diagrama de Kekulé o quimiograf. […] Dono una regla per a la multiplicació geomètrica de grafs, és a dir, per construir un graf per al producte d'invariants o covariants donats. […]	»
— Sylvester, Chemistry and Algebra (Nature)

El primer llibre de text sobre teoria de grafs fou escrit per Dénes Kőnig, i publicat el 1936. Un altre llibre de Frank Harary, publicat el 1969, fou "considerat com el llibre de text definitiu sobre la matèria", i va aconseguir que els matemàtics, químics, enginyers elèctrics i científics socials parlessin un llenguatge comú. Harary va cedir-ne tots els drets al Premi Pólya.

Un dels problemes de teoria de grafs més famós i més estimulant és el problema dels quatre colors: "És o no cert que qualsevol mapa dibuixat al pla pot tenir les seves regions pintades amb quatre colors, de tal manera que dues regions qualssevol amb frontera comuna tinguin colors diferents?" Aquedt problema fou proposat per primer cop per Francis Guthrie l'any 1852, i el seu primer registre escrit és una carta de De Morgan a Hamilton el mateix any. Se n'han proposat moltes demostracions incorrectes, incloses les de Cayley, Kempe i altres. L'estudi i la generalització d'aquest problema realitzats per Tait, Heawood, Ramsey i Hadwiger van portar a l'estudi de les coloracions dels grafs immersos en superfícies amb un gènere arbitrari. La reformulació de Tait va generar una nova classe de problemes, els problemes de factorització, estudiats especialment per Petersen i Kőnig. Les obres de Ramsey sobre coloracions i més especialment els resultats obtinguts per Turán el 1941 van originar una altra branca de la teoria de grafs, la teoria de grafs extremals.

El problema dels quatre colors va quedar sense solució durant més d'un segle. L'any 1969, Heinrich Heesch va publicar un mètode per resoldre el problema mitjançant l'ús d'ordinadors. L'any 1976, Kenneth Appel i Wolfgang Haken van publicar una demostració, que feia ús del concepte de "descàrrega" desenvolupat per Heesch. La demostració incloïa comprovar per ordinador les propietats de 1.936 configuracions, cosa que no fou acceptada completament en aquella època a causa de la seva complexitat. Vint anys després, Robertson, Seymour, Sanders i Thomas van proporcionar una demostració més senzilla amb 633 configuracions.

El desenvolupament autònom de la topologia entre 1860 i 1930 va obrir el camí a la teoria de grafs, amb les obres de Jordan, Kuratowski i Whitney. Un altre factor important en el desenvolupament comú de la teoria de grafs i la topologia va venir de l'ús de les tècniques de l'àlgebra moderna. El primer exemple d'aquest ús prové de l'obra del físic Gustav Kirchhoff, qui va publicar el 1845 les seves lleis de Kirchhoff per calcular el voltatge i el corrent en circuits elèctrics.

La introducció dels mètodes probabilístics en la teoria de grafs, especialment en l'estudi de Erdős i Rényi sobre la probabilitat asimptòtica de la connectivitat de grafs, va originar una altra branca, anomenada teoria de grafs aleatoris, que ha estat una font de molts resultats de la teoria de grafs.

Representació gràfica

Els grafs es representen visualment dibuixant un punt o cercle per a cada vèrtex, i un segment entre dos vèrtexs si estan connectats per una aresta. Si el graf és dirigit, el sentit es representa mitjançant una fletxa.

Cal no confondre una representació gràfica d'un graf amb el mateix graf (l'estructura abstracta, no visual), ja que existeixen diverses formes d'estructurar-ne la representació gràfica. El que importa és quins vèrtexs estan connectats als altres, i no la seva disposició exacta. A la pràctica, és difícil determinar si dos gràfics representen el mateix graf. Depenent del problema que calgui resoldre, algunes representacions gràfiques poden ser més adequades i fàcils d'entendre que d'altres.

L'obra de William T. Tutte tingué una gran influència en l'àrea de la representació gràfica de grafs. Entre altres contribucions, Tutte va introduir l'ús de mètodes de l'àlgebra lineal per obtenir representacions gràfiques.

Les representacions gràfiques juguen també un rol essencial en problemes sobre el nombre de creuament i les seves generalitzacions. El nombre de creuament d'un graf és el mínim nombre d'interseccions entre arestes que ha de contenir una representació gràfica al pla d'un graf. Per definició, el nombre de creuament d'un graf planar és zero.

També es poden considerar representacions gràfiques sobre superfícies diferents del pla.

Estructures de dades basades en la teoria de grafs

Article principal: Graf (estructura de dades)

Existeixen diferents formes d'emmagatzemar grafs en un ordinador. L'estructura de dades utilitzada depèn tant de l'estructura del graf com de l'algoritme utilitzat per manipular-lo. En teoria, hom pot distingir entre estructures de llista i de matriu, però a la pràctica la millor estructura acostuma a ser una combinació de les dues. Les estructures basades en llistes són més útils per a grafs dispersos, ja que necessiten menys memòria per emmagatzemar-los. Les estructures matricials, per altra banda, proporcionen un accés més ràpid, però poden consumir més memòria.

Les estructures de llista inclouen la llista d'incidència, una llista de parells de vèrtexs, i la llista d'adjacència, que llista de manera separada els veïns de cada vèrtex.

Les estructures matricials inclouen la matriu d'incidència, una matriu de zeros i uns, on les files representen els vèrtexs i les columnes representen les arestes; i la matriu d'adjacència, on tant les files com les columnes representen els vèrtexs. En ambdós casos, un 1 representa dos objectes adjacents i un 0 indica dos objectes no adjacents (o, en el cas de grafs dirigits, +1 o -1 per expressar l'orientació de cada aresta, i 0 si els objectes no són adjacents). La matriu Laplaciana és una versió modificada de la matriu d'adjacència, que incorpora informació sobre els graus dels vèrtexs, i és útil en alguns càlculs com el teorema de Kirchhoff sobre el nombre d'arbres d'expansió d'un graf. La matriu de distàncies, de la mateixa manera que la matriu d'adjacència, té files i columnes que representen els vèrtexs, però, en comptes de tenir entrades amb valor 0 o 1, contenen la longitud d'un camí mínim entre dos vèrtexs.

Problemes de teoria de grafs

Enumeració

Existeix una àmplia literatura sobre l'enumeració de grafs: el problema de comptar els grafs que satisfan unes determinades condicions. Algunes d'aquestes obres es poden trobar a Harary & Palmer 1973.

Subgrafs, grafs induïts i menors

Un problema comú, conegut com a problema d'isomorfisme de subgrafs, és trobar un graf fixat com a subgraf d'un graf donat. Una raó és que moltes propietats dels grafs són hereditàries per a subgrafs, la qual cosa vol dir que un graf té la propietat si i només si tots els seus subgrafs també la tenen. Malauradament, el problema de trobar subgrafs maximals d'un cert tipus sol ser un problema NP-complet. Per exemple:

• El problema de trobar el major subgraf complet es coneix com a problema de la clique (NP-complet).

Un problema similar consisteix a trobar els subgrafs induïts d'un determinat graf. De nou, algunes propietats importants dels grafs s'hereden als subgrafs induïts, la qual cosa significa que un graf té una propietat si i només si tots els seus subgrafs induïts la tenen. El problema de trobar subgrafs induïts maximals d'un cert tipus també acostuma a ser NP-complet. Per exemple:

• Trobar el subgraf induït maximal sense arestes, o conjunt independent es coneix amb el nom de problema del conjunt independent (NP-complet).

Un altre problema, el problema del menor contingut, consisteix a trobar un graf fixat com a menor d'un graf donat. Un menor o subcontracció d'un graf és qualsevol graf obtingut a partir d'un subgraf i contraient-ne algunes arestes. Moltes propietats dels grafs són hereditàries per a menors, la qual cosa vol dir que un graf té una propietat si i només si tots els seus menors també la tenen. Per exemple:

• Un graf és planar si conté un menor que no sigui ni el graf bipartit complet K_3,3 (vegeu el problema de les tres cases) ni el graf complet K₅.

Una altra classe de problemes té a veure amb fins a quin punt es pot reconstruir un graf si se n'ha eliminat algun punt. Per exemple:

• La conjectura de la reconstrucció

Coloració de grafs

Molts problemes tenen a veure amb diferents formes d'acolorir grafs, per exemple:

• El teorema dels quatre colors
• La conjectura d'Erdős–Faber–Lovász
• La conjectura de la coloració total, també anomenada conjectura de Behzad
• La conjectura de Hadwiger

Problemes d'encaminament

• Problema del camí hamiltonià
• Arbre recobridor mínim
• Problema d'inspecció de rutes (també conegut com a "problema del carter xinès")
• Els set ponts de Königsberg
• Problema del camí més curt
• Problema de l'arbre de Steiner
• Problema de les tres cases
• Problema del viatjant de comerç (NP-complex)

Flux de xarxes

Existeixen multitud de problemes relacionats amb el concepte de xarxa de flux, per exemple:

• Teorema de flux màxim tall mínim

Problemes de visibilitat

• Problema del guarda del museu

Problemes de recobriment

Els problemes de recobriment en grafs són casos especials dels problemes de trobar subgrafs, i acostumen a estar fortament relacionats amb el problema de la clique o amb el problema del conjunt independent.

• Problema del conjunt de cobertura
• Problema de la cobertura de vèrtexs

Problemes de descomposició

El concepte de descomposició, definida com la partició del conjunt d'arestes d'un graf (amb els vèrtexs necessaris per a cada part), admet una multitud de variants. De vegades s'exigeix descompondre un graf en subgrafs isomorfs a un cert graf; per exemple, descompondre un graf complet en cicles hamiltonians. Altres problemes especifiquen una família de grafs en els quals s'ha de descompondre un graf donat, per exemple, una família de cicles, o descompondre un graf complet K_n en n − 1 arbres especificats que tinguin, per exemple, 1, 2, 3, …, n − 1 arestes.

Alguns problemes concrets de descomposició són:

• Arboricitat, una descomposició en el menor nombre possible de boscos.
• Coloració d'arestes, una descomposició en el menor nombre possible d'aparellaments.
• Factorització de grafs, una descomposició d'un graf regular en subgrafs regulars de graus donats.

Classes de grafs

Molts problemes tenen a veure amb caracteritzar els membres de diverses classes de grafs. Alguns exemples són:

• Enumerar els membres d'una classe.
• Caracteritzar una classe en funció d'estructures prohibides.
• Determinar relacions entre classes (és a dir, si una propietat de grafs n'implica una altra).
• Trobar algoritmes eficients per decidir la pertinença o no d'un graf a una classe.
• Trobar representacions per a membres d'una classe.

Influència dels grafs en la recollida d'escombraries

Els grafs tenen moltes utilitats al dia a dia i, a més, se’n poden trobar-ne més si s'apliquen propietats de grafs a situacions quotidianes. Es proposa implicar els grafs en una feina tan imprescindible com recollir l'escombraria amb el camió municipal, ubicada a Igualada tot respectant els sentits de circulació actual. A part, fem servir Geogebra, una aplicació matemàtica que ens ajudarà en aquesta tasca.

En la imatge destaquem en punts de color ocre les interseccions, en vermell els contenidors i en blau, l'orientació de les fletxes.

Un cop s'han posicionat tots els punts, en el Geogebra escrivim la instrucció : Viajante[<Lista de Puntos>]. Aquesta comanda ens determina el recorregut que passa per ells i no els repeteix en cap cas.

Conseqüentment, queda un graf tancat que conté un camí eulerià i un cicle hamiltonià com es pot apreciar en la fotografia:

Malauradament Geogebra només aporta un camí que és el més òptim i per tant, no ens dona una altra possibilitat. Si els sentits dels carrers fossin diferents, i tots fossin invertits, es podria fer el mateix circuit. Ara bé, si només un carrer fos canviat de sentit, s'hauria de replantejar tot el graf, tornant a calcular el camí més adequat.

Aquesta contribució mostra una aplicació de la teoria de grafs fruit d'un treball més ampli realitzat a l'assignatura Fonaments Matemàtics curs 2016-17 sota la direcció del Dr. Joan Gómez Urgellés amb l'alumne Martí Miquel Martínez.

Bibliografia

• Berge, Claude. Théorie des graphes et ses applications. II. París: Dunod, 1958 (Collection Universitaire de Mathématiques).  (anglès) Wiley 1961; Methuen & Co, New York 1962; (rus) Moscow 1961; (castellà) Mexico 1962; (romanès) Bucharest 1969; (xinès) Shanghai 1963.
• Biggs, Norma L.; Lloyd, E. Keith; Wilson, Robin J. Graph Theory, 1736–1936. Oxford University Press, 1986. ISBN 9780198539162. 
• Bondy, J.A.; Murty, U.S.R.. Graph Theory. Springer, 2008. ISBN 978-1-84628-969-9. 
• Bondy, Riordan, O.M. Mathematical results on scale-free random graphs in "Handbook of Graphs and Networks" (S. Bornholdt and H.G. Schuster (eds)), Wiley VCH, Weinheim, 1st ed., 2003. 
• Cáceres, José; Hernando, Carmen; Mora, Mercè; Pelayo, Ignacio M.; Puertas, María L.; Seara, Carlos (2006). «On geodetic sets formed by boundary vertices». Discrete Mathematics. 306 (2): 188-198. doi:10.1016/j.disc.2005.12.012.
• Chartrand, Gary. Introductory Graph Theory. Dover, 1985. ISBN 0-486-24775-9. 
• Gibbons, Alan. Algorithmic Graph Theory. Cambridge University Press, 1985. ISBN 9780521288811. 
• Havlin, Shlomo; Cohen, Reuven. Complex Networks: Structure, Robustness and Function. Cambridge University Press, 2010. ISBN 9780521841566. 
• Golumbic, Martin. Algorithmic Graph Theory and Perfect Graphs. Academic Press, 1980. ISBN 9780122892608. 
• Harary, Frank. Graph Theory. Reading (Massachusetts): Addison-Wesley, 1969. ISBN 0201027879 [Consulta: 30 març 2016].  Arxivat 2017-02-07 a Wayback Machine.
• Harary, Frank; Palmer, Edgar M. Graphical Enumeration. Nova York: Academic Press, 1973. ISBN 978-1483240329. 
• Mahadev, N.V.R.; Peled, Uri N. Threshold Graphs and Related Topics. North-Holland, 1995. ISBN 9780444892874. 
• Newman, Mark. Networks: An Introduction. Oxford University Press, 2010. ISBN 9780199206650. 

Vegeu també

• Base de dades orientada a grafs
• Glossari de teoria de grafs
• Llista de temes sobre la teoria de grafs
• Lema de Berge

Enllaços externs

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Teoria de grafs

• Teoria de grafs amb exemples
• Michiel Hazewinkel (ed.). Graph theory. Encyclopedia of Mathematics (en anglès). Springer, 2001. ISBN 978-1-55608-010-4.