Linear feedback shift register
LFSR significa linear feedback shift register, que es tradueix com: registre de desplaçament amb retroalimentació lineal. És un registre de desplaçament en el qual l'entrada és un bit provinent d'aplicar una funció de transformació lineal a un estat anterior.
El valor inicial es denomina llavor i, com la forma d'operar el registre és determinística, la seqüència de valors produïts està completament determinada per l'estat actual o l'estat anterior. La seqüència té un període de repetició, és a dir que la seqüència torna a generar i es repeteix indefinidament. Quan el període de repetició és màxim, aquest LFSR té interès criptogràfic.
Com funciona un LFSR[modifica]
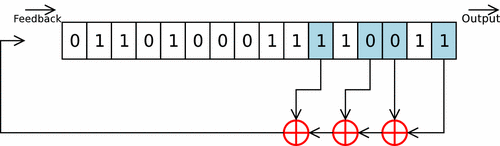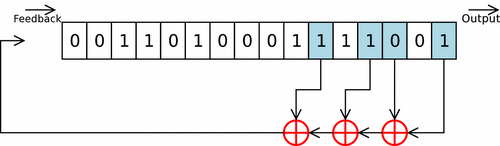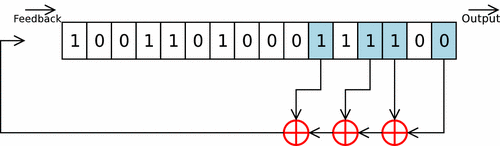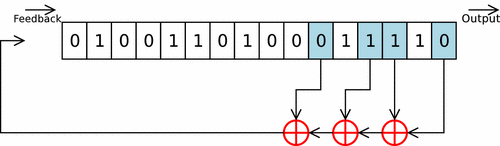
Es té el polinomi seqüència [16,14,13,11]. La seqüència tap d'un LFSR es pot representar com un polinomi mod 2. Això vol dir que els coeficients del polinomi han de ser 1s o 0s. Això es diu polinomi de realimentació o característica polinomial. Per exemple, si els taps estan en les posicions dels bits: 16, 14, 13 i 11, el polinomi LFSR resultant és:
Les sortides que influeixen en l'entrada, es denominen taps. Són les que apareixen en el polinomi. I s'indiquen en blau en l'esquema inferior.
- Si el polinomi és primitiu, si i només si, el LFSR és màxim o, cosa que és equivalent, té període màxim.
- El LFSR només serà màxim si el nombre de taps és parell.
- Els valors de tap en un LFSR màxim són coprimers.
- Hi pot haver més d'una seqüència tap que faci màxim al LFSR per aquesta longitud determinada.
- Un cop trobada una seqüència tap màxima, automàticament segueix una altra. Si la seqüència tap, en un LFSR n bits, és [a, A, B, C], llavors la seqüència mirror corresponent és [a, nA, nB, nC]. Per exemple, la seqüència tap [32,3,2,1], té el seu homòleg [32,29,30,31]. Tots dos donen com a resultat període màxim.
Exemple de programació en C[modifica]
#include <stdint.h>
uint16_t lfsr = 0xACE1u;
unsigned bit;
unsigned period = 0;
do {
/* taps: 16 14 13 11; Polinomi: x^16 + x^14 + x^13 + x^11 + 1 */
bit = ((lfsr >> 0) ^ (lfsr >> 2) ^ (lfsr >> 3) ^ (lfsr >> 5)) & 1;
lfsr = (lfsr >> 1) | (bit << 15);
++period;
} while(lfsr != 0xACE1u);
Propietats del flux de sortida[modifica]
Un LFSR es pot caracteritzar de forma polinòmica segons siguin les seves connexions i els valors dels registres.
Es defineix el polinomi d'Estat com:
El polinomi d'estat mostra el valor dels registres. De la mateixa manera es defineix el polinomi de Connexions com:
On cada coeficient val 0 o 1 depenent de si hi ha connexió o no. Cal notar que el polinomi de connexions és sempre un grau més gran que el d'estat.
D'aquesta manera un LFSR amb n registres de desplaçament tindrà com a mínim 2 connexions la de i la de . La connexió de és necessària perquè sense ella el primer registre sempre valdria zero i per tant no influiria en el comportament del LFSR. La connexió és necessària perquè assegura la retroalimentació del LFSR. Si aquest coeficient valgués 0 (o, cosa que és el mateix, si no hi hagués aquesta connexió), el LFSR ja no seria de grau n +1.
D'aquesta manera per passar d'un estat al següent els registres es desplacen. Aquest desplaçament es pot expressar en forma polinòmica com una multiplicació per D. El polinomi resultant té grau n +1 igual que el polinomi de connexions. Això és un problema, ja que el polinomi d'estat ha de ser de grau n. Això se soluciona fent que el polinomi resultant sigui mòdul de C(D).
Si és el polinomi d'Estat a l'estat i-èsim, en forma polinòmica el desplaçament del polinomi d'Estat s'expressa així:
Com el grau ha de ser menor que n +1 es fa el mòdul de C(D):
Amb el que resulta un polinomi de grau n com a màxim.
Usos criptogràfics[modifica]
Fa temps que LFSR s'usa com Generador de nombres pseudoaleatoris per xifrador de flux, especialment en criptografia militar, ja que la seva construcció és molt fàcil, basant-se en circuits electrònics i electromecànics simples.
Aplicacions en comunicacions[modifica]
El sistema de Posicionament Global, GPS utilitza un LFSR per transmetre ràpidament una seqüència que indica time offsets d'alta precisió relativa.
Per mantenir transmissions digitals formades de patrons d'energia que poden interrompre altres transmissions digitals o analògiques. LFSR s'usa per fer més aleatori el flux de bits de sortida (aquesta tècnica es coneix com a Scrambling).
Sistemes de broadcasting digital que fan servir LFSR:
- NICAM (digital àudio system for television)
- ATSC (HDTV transmission system - North America)
- DVB-T (HDTV transmission system - Europe, Australasia)
Altres sistemes de comunicació digital que fan servir LFSR:
- IBS (INTELSAT business service)
- IDR (Intermedaite Data Rate service)
- SDI (Serial Digital Interface transmission)
- Data transfer over PSTN (according to the ITU-T V recommendations)