Punt de contacte quàntic

Un punt de contacte quàntic (en anglès Quantum Point Contact o QPC) és una constricció estreta entre dos regions amples elèctricament conductores, amb una amplada comparable a la longitud d'ona electrònica (de nano a micròmetres). La importància del QPC resideix en que proven la quantització de la conductància balística en mesoscopic sistemes. La seva conductància està quantitzada en unitats de $2e^{2}/h$, conegut com a quantum de conductància.

Els primers informes de punts de contacte quàntics van ser publicats el 1988 per un equip holandès de Delft Universitat de Tecnologia i Philips Research, i, independentment, per un equip britànic del Cavendish Laboratori (Wharam et al.).

Conductància del punt de contacte com a funció del voltatge de porta. La condunctància mostra esglaons múltiples de $e^{2}\pi /\hbar$.

Aquesta quantització és reminiscent de la quantització de la conductància de Hall, però és mesurada en l'absència d'un camp magnètic. La quantització de la conductància de camp-zero i la transició llisa a l'efecte Hall quàntic en aplicar un camp magnètic són, essencialment, conseqüències de la equipartició de corrent amb un número enter de propagació de modes en la constricció.

Fabricació

Hi ha diverses maneres diferents de fabricar un QPC. Es pot fer separant un conductor fins que es trenca. El punt en el qual es trenca és el que forma el contact point. En una manera més controlada, es poden formar en un gas d'electró bidimensional (2DEG), és a dir en GaAs/AlGaAs heterostructures. Aplicant un voltatge adequat, el gas d'electrons pot ser localment exhaurit i molts tipus diferents de regions de conductància poden ser creades en el pla del 2DEG, entre ells punts quàntics i punts de contacte quàntic. Un altre manera de crear un QPC és col·locant la punta d'un microscopic d'escaneig tunelador a prop de la superfície del conductor.

Propietats

Geomètricament, un punt de contacte quàntic és una constricció en la direcció transversal que presenta una resistència al moviment d'electrons. Aplicant un voltatge $V$ a través del punt de contacte s'indueix un flux d'electrons, la magnitud d'aquest corrent és donada per $I=GV$, on $G$ és la conductància del contacte. Aquesta fórmula s'assembla a la llei de l'ohm per resistors macroscòpics. Tanmateix, hi ha una diferència fonamental aquí resultant de la petita mida de sistema, la qual cosa requereix una anàlisi a través de la mecànica quàntica.

Transport balístic clàssic a través d'un punt de contacte quàntic induït per una diferència de concentració.

Corrent net a través d'un punt de contacte quàntic, mostrat en la regió ombrejada. Les sub-bandes unidimensionals es corresponen als parells de línies horitzontals a $k_{y}=\pm n\pi /W$ , amb n = 1, 2, . ., N, sent N el número màxim de modes permesos per l'energia de Fermi.

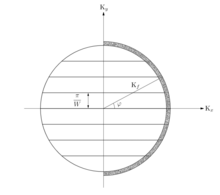
El més comú és estudiar QPC en gasos bidimensional d'electrons (2DEG). A més, requereix una descripció mecànica quàntica del sistema que resulta en la quantització de la conductància. Segons la descripció de la mecànica quàntica, el corrent a través del punt de contacte és divideix de forma igual entre les subandes de conducció 1-dimensionals, o modes transversals, en la constricció.

La discussió anterior no té en compte transicions possibles entre modes. Segons Landauer la fórmula de fet pot ser generalitzada per expressar aquestes transicions possibles ,

$G={2e^{2} \over h}\sum _{n,m}|T_{n,m}|^{2}$

on $T_{n,m}$ és la matriu de transició que incorpora probabilitats no nules de transmissió de mode n a m.

A voltatges i temperatures baixes, els electrons lliures no dispersats que contribueixen al corrent tenen una longitud d'ona/moment/energia anomenada longitud d'ona/moment/energia de Fermi. De manera semblant a una guia d'ona, el confinament transvers en els PCQ resulta en una "quantització" del moviment transvers—el moviment transvers no pot variar contínuament, en canvi, consisteix en una sèrie de modes discrets. L'analogia de la guia d'ones és aplicable en tant la coherència no és perdi a través de dispersions, e.g., per un defecte o una trampa electrònica. L'ona de l'electró només pot passar a través de la constricció si interfereix constructivament, el qual per una amplada donada de constricció, només passa per un número concret de modes $N$. El corrent portat per aquest estat quàntic és el producte de la velocitat vegades la densitat d'electró. Aquestes dues quantitats per elles mateixes difereixex d'un mode a l'altre, però el seu producte és independent del mode. En conseqüència, cada estat contribueix la mateixa quantitat per direcció d'espín a la conductància total $e^{2}/h$$G=NG_{Q}$.

Això és un resultat fonamental; la conductància no assoleix valors arbitraris sinó que es quantitza en múltiples del quàntum de conductància, el qual és expressat a través de la càrrega d'electró i la constant de Planck $G_{Q}=2e^{2}/h$$e$$h$. El número d'enter N és determinat per l'amplada del PQC i és aproximadament igual a l'amplada dividida per la meitat de la longitud d'ona de l'electró. Com a funció de l'amplada del PCQ (o voltatge de porta en el cas de dispositius d'heterostructura GaAs/AlGaAs), la conductància mostra un comportament d'escala quant més i més modes (o canals) contribueixin al transport d'electrons. El l'alçada de l'esglaó ve donada per $G_{Q}$.

Al incrementar la temperatura, un pot trobar experimentalment que l'esglaó obté un pendent finit fins que ja no es poden distingir. Això és una conseqüència de la contribució térmica de la distribució de Fermi-Dirac. Els esglaons de la conductància desaparèixen per T >∼ ∆E/4kB ∼ 4 K (on ∆E és la subanda partida al nivell de Fermi). Això ha estat confirmat experimentalment i numéricament).

Un camp magnètic extern aplicat als punts de contacte quàntic provoca una degeneració a l'espín i provoca esglaons mig-enters en la conductància. A més a més, el nombre $N$ de modes que contribueixen esdevé més petit. Per camps magnètics grans, $N$ és independent de l'amplada de la constricció, donat per la teoria de l'efecte Hall quàntic. Una característica interessant es que, encara que no s'ha entés encara plenament, és un esglaó a $0.7G_{Q}$,el tan-va cridar 0.7-estructura.

Aplicacions

Apart d'estudiar els fonaments del transport de càrrega en conductors mesoscòpics, els punts de contacte quàntic poden fer-se servir com detectors de càrrega extremadament sensitius. Ja que la conductància a través del contacte depends fortament en la mida de la constricció, qualsevol fluctuació del potencial (per exemple, creat per altres electrons) a la proximitat influirà al corrent a través del dispositiu. És possible detectar electrons individuals amb un muntatge com aquest. Quant a computació quàntica en sistemes d'estat sòlid, els punts de contacte quàntic poden ser fets servir com dispositius de lectura per l'estat d'un bit quàntic (qubit). A la física de dispositius, la configuració de punts de contacte quàntic és utilitzada per demostrar un transistor de transport completament balístic. Una altra aplicació del dispositiu és el seu ús com un interruptor. Un cable de niquel es porta suficientment a prop d'una superfície d'or i aleshores, utilitzant un actuador piezoelèctric, la distància entre el cable i la superfície es pot canviar i aleshores, les característiques de transport del dispositiu canvien entre efecte tunel electrònic i balístic.