Distribució de grau
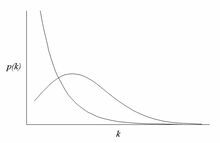
En l'estudi de grafs i xarxes complexes, el grau d'un vèrtex en una xarxa és el nombre de connexions associades a un vèrtex. Si en una xarxa es fes un recompte del nombre de nodes que tenen grau k, es tindria la distribució de grau d'un graf, que seria entesa igualment com la distribució de probabilitat d'un grau en una xarxa.[1]
Definició
[modifica]El grau d'un node en una xarxa (sovint anomenat incorrectament com la connectivitat) és el nombre de connexions d0un vèrtex o node amb altres nodes. Si una xarxa és dirigida, això significa que hi haurà enllaços que surtin i enllaços que entrin als nodes i per tant es mencionarà que existeixen graus d'entrada i graus de sortida en funció de la disposició dels enllaços entrants i sortints dels nodes.
La distribució de grau en una xarxa es representa normalment com P(k) i és definida com la fracció de nodes en la xarxa amb un cert grau k. És com dir que si la xarxa té una quantitat n de nodes en total i nk d'ells tenen grau k, llavors es té que P(k) = nk/n, és a dir, que la probabilitat que un node tingui grau k (P(k)) és igual al nombre de nodes que tenen grau k entre el nombre total de nodes. La mateixa informació es presenta en forma d'una distribució acumulativa de grau, que indica la fracció de nodes amb un grau major o igual que k.[2]
Tipus
[modifica]Una de les propietats més importants de l'anàlisi de l'estructura de les xarxes és tal vegada la distribució de grau , ja que proporciona la probabilitat que un node elegit a l'atzar de la xarxa tingui exactament k connexions (o veïns). S'han pogut classificar les xarxes en funció de la distribució de grau en diverses topologies, les més conegudes són:
- Topologia de Poisson: es consideren importants en ser les primeres que es van començar a utilitzar en el model d'Erdős-Rényi en la dècada dels anys 50. Per aquesta raó de vegades se'ls anomena xarxes de tipus Erdős-Rényi. Malgrat tot, la representació de xarxes d'aquest tipus no es correspon amb la distribució de grau de les xarxes que apareixen en la natura. La seva distribució de grau és la següent:
- Topologia exponencial: es produeix aquesta topologia en les xarxes evolucionistes en el temps sempre que cada nou node que s'afegeix té la mateixa probabilitat de ser enllaçat que la resta. A aquesta propietat se la denomina enllaç igualitari. La seva distribució de grau és:
- Topologia lliure d'escala: els estudis realitzats per Lászlo Barabási sobre les xarxes complexes van donar lloc a estudis de xarxes amb aquest tipus de distribució de grau. Algunes de les xarxes més comunes de la natura mostren aquesta distribució, com pot ser internet, les xarxes socials, etc. La seva distribució de grau és:
Bibliografia
[modifica]- Albert, R.; Barabasi, A.-L. «Statistical mechanics of complex networks». Reviews of Modern Physics, 74, 2002, pàg. 47-97.
- Dorogovtsev, S.; Mendes, J. F. F. «Evolution of networks». Advances in Physics, 51, 2002, pàg. 1079-1187.
- Newman, M. E. J. «The structure and function of complex networks». SIAM Review, 45, 2003, pàg. 167-256.[Enllaç no actiu]
Referències
[modifica]- ↑ "Linked: The New Science of Networks", Albert-László Barabási, Basic Books, 2003, ISBN 0-7382-0667-9
- ↑ "Random Networks with Tunable Degree Distribution and Clustering", Erik McCullough Volz, Cornell University, Jan, 2005




