Distribució exponencial

Distribució exponencial

Funció de probabilitat
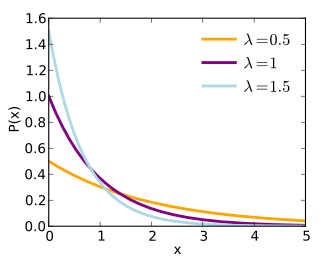Funció de distribució de probabilitat
Paràmetres	$\lambda> 0 \,$
Domini	$[0, \infty) \!$}
Funció de probabilitat (fp)	$\lambda e^{- \lambda x}$
Funció de distribució (cdf)	$1 - e^{- \lambda x}$
Mitjana	$1/\lambda \,$
Mediana	$\ln (2)/\lambda \,$
Moda	$0 \,$
Variància	$1/\lambda^2 \,$
Coeficient de simetria	$2 \,$
Curtosi	$6 \,$
Entropia	$1 - \ln (\lambda) \,$
Funció generadora de moments (mgf)	$\left (1 - \frac{t}{\lambda}\right)^{-1}\,$
Funció característica	$\left (1 - \frac{it}{\lambda}\right)^{-1}\,$

A l'entorn d'estadística la distribució exponencial és una distribució de probabilitat contínua amb un paràmetre $\lambda> 0$ la funció de densitat és:

$f(x)=\left\{\begin{matrix} \lambda e^{-\lambda x} & \ \ \mbox{per a } x \ge 0 \\ 0 & \ \ \mbox{o altrament} \end{matrix}\right.$

La seva funció de distribució és: $F(x)= P(X \le x)=\left\{\begin{matrix} 0 & \mbox{per a }x < 0 \\ 1-e^{-\lambda x} & \mbox{per a }x \ge 0 \end{matrix}\right.$

On $i$ representa el nombre i.

El valor esperat i la variància d'una variable aleatòria X amb distribució exponencial són:

• $E [X] = \frac{1}{\lambda}$
• $V (X) = \frac{1}{\lambda^2}$

Exemple

Exemples per a la distribució exponencial és la distribució de la longitud dels intervals de variable contínua que transcorre entre l'ocurrència de dos successos "rars", que es distribueixen segons la distribució de Poisson.

Calcular variables aleatòries

Es poden calcular una variable aleatòria de distribució exponencial $x$ per mitjà d'una variable aleatòria de distribució uniforme $u = U (0,1)$:

$X =- \frac{\ln o}{\lambda}$

Relacions

La suma de $k$ variables aleatòries independents de distribució exponencial amb paràmetre $\lambda$ és una variable aleatòria de distribució gamma.

Vegeu també

• Procés de Poisson.
• Distribució de Poisson.

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Distribució exponencial