Distribució SU de Johnson
Funció de densitat de probabilitat  | |
Funció de distribució de probabilitat 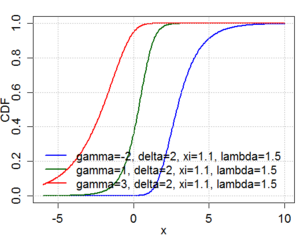 | |
| Paràmetres | (real) |
|---|---|
| Suport | |
| fdp | |
| FD | |
| Esperança matemàtica | |
| Mediana | |
| Variància | |
La distribució SU de Johnson és una família de quatre paràmetres de distribució de probabilitats investigada per primera vegada per N. L. Johnson el 1949.[1][2] Johnson la va proposar com una transformació de la distribució normal:[3]
on .
Generació de variables aleatòries
[modifica]Sigui U una variable aleatòria que es distribueix uniformement en l'interval unitari [0, 1]. Les variables aleatòries SU de Johnson poden generar-se a partir d'U de la manera següent:
on Φ és la funció de distribució acumulada de la distribució normal.
Distribució SB de Johnson
[modifica]Norman Lloyd Johnson va ser el primer en proposar la transformació:[1]
on .
Les variables aleatòries SB de Johnson es poden generar a partir d'U de la següent manera:
on Φ és la funció de distribució acumulada de la distribució normal. La distribució SB de Johnson és convenient per a distribucions de Platykurtic (curtosi).
Referències
[modifica]- ↑ 1,0 1,1 Johnson, N. L. «Systems of Frequency Curves Generated by Methods of Translation». Biometrika, 36, 1/2, 1949, pàg. 149–176. DOI: 10.2307/2332539. JSTOR: 2332539.
- ↑ Johnson, N. L. «Bivariate Distributions Based on Simple Translation Systems». Biometrika, 36, 3/4, 1949, pàg. 297–304. DOI: 10.1093/biomet/36.3-4.297. JSTOR: 2332669.
- ↑ Johnson (1949) "Systems of Frequency Curves...", p. 158
Bibliografia
[modifica]- Hill, I. D.; Hill, R.; Holder, R. L. «Algorithm AS 99: Fitting Johnson Curves by Moments». Journal of the Royal Statistical Society. Series C (Applied Statistics), 25, 2, 1976.
- Jones, M. C.; Pewsey, A. «Sinh-arcsinh distributions». Biometrika, 96, 4, 2009, pàg. 761. DOI: 10.1093/biomet/asp053.(Preprint)
- Tuenter, Hans J. H. «An algorithm to determine the parameters of SU-curves in the Johnson system of probability distributions by moment matching». The Journal of Statistical Computation and Simulation, 70, 4, novembre 2001, pàg. 325–347. DOI: 10.1080/00949650108812126.












