Distribució estable

Estable

Funció de densitat de probabilitat Simetria de la distribució $\alpha$-estable amb factor d'escala unitat Distribucions estables centrades esbiaixades amb factor d'escala unitat
Funció de distribució de probabilitat Funció de distribució per a la distribució $\alpha$-estable amb factor d'escala unitat 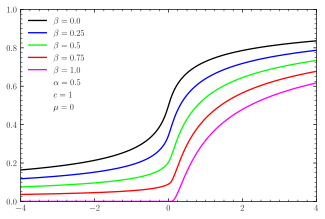Factors de distribució per a distribucions estables centrades esbiaixades
Tipus	Distribució estable multivariant
Epònim	Paul Lévy
Paràmetres	$\alpha \in (0,2]$ — paràmetre d'estabilitat $\beta$ ∈ [−1, 1] — paràmetre d'asimetria (tingueu en compte que l'asimetria no està definida) c ∈ (0, ∞) — paràmetre d'escala μ ∈ (−∞, ∞) — paràmetre de localització
Suport	x ∈ [μ, +∞) si $\alpha <1$ i $\beta =1$ x ∈ (-∞, μ] si $\alpha <1$ i $\beta =-1$ x ∈ R altrament
fdp	no es pot expressar analíticament, tret d'alguns valors de paràmetres
FD	no es pot expressar analíticament, tret d'alguns valors de paràmetres
Esperança matemàtica	μ quan $\alpha >1$, altrament no és definida
Mediana	μ quan $\beta =0$, altrament no es pot expressar analíticament
Moda	μ quan $\beta =0$, altrament no es pot expressar analíticament
Variància	2c2 quan $\alpha =2$, altrament és infinita
Coeficient de simetria	0 quan $\alpha =2$, altrament no és definida
Curtosi	0 quan $\alpha =2$,altrament no és definida
Entropia	no es pot expressar analíticament, excepte per a determinats valors de paràmetres
FGM	$\exp \!\left(t\mu +c^{2}t^{2}\right)$ quan $\alpha =2$, altrament no és definida
FC	$\exp \!{\Big [}\;it\mu -|c\,t|^{\alpha }\,(1-i\beta \operatorname {sgn}(t)\Phi )\;{\Big ]},$ quan $\Phi ={\begin{cases}\tan {\tfrac {\pi \alpha }{2}}&{\text{si }}\alpha \neq 1\\-{\tfrac {2}{\pi }}\log |t|&{\text{si }}\alpha =1\end{cases}}$

En teoria de la probabilitat, es diu que una distribució és estable si una combinació lineal de dues variables aleatòries independents amb aquesta distribució té la mateixa distribució, fins als paràmetres de localització i escala. Es diu que una variable aleatòria és estable si la seva distribució és estable. La família de distribucions estables també es coneix de vegades com la distribució alfa-estable de Lévy, després de Paul Lévy, el primer matemàtic que la va estudiar.

Dels quatre paràmetres que defineixen la família, la major atenció s'ha centrat en el paràmetre d'estabilitat, $\alpha$ (veure panell). Les distribucions estables tenen $0<\alpha \leq 2$, amb el límit superior corresponent a la distribució normal, i $\alpha =1$ a la distribució de Cauchy. Les distribucions tenen variància indefinida per $\alpha <2$, i significa indefinida per $\alpha \leq 1$ }. La importància de les distribucions de probabilitat estables és que són "atractors" per a sumes correctament normades de variables aleatòries independents i distribuïdes de manera idèntica (iid). La distribució normal defineix una família de distribucions estables. Segons el teorema del límit central clàssic, la suma correctament normada d'un conjunt de variables aleatòries, cadascuna amb variància finita, tendirà cap a una distribució normal a mesura que augmenta el nombre de variables. Sense el supòsit de variància finita, el límit pot ser una distribució estable que no sigui normal. Mandelbrot es va referir a aquestes distribucions com a "distribucions paretianes estables", després de Vilfredo Pareto. En particular, es va referir a aquells que s'han esbiaixat al màxim en la direcció positiva $1<\alpha <2$ com a "distribucions de Pareto-Lévy", que considerava millors descripcions dels preus de les accions i de les mercaderies que les distribucions normals.

Definició

Una distribució no degenerada és una distribució estable si compleix la propietat següent:

Siguin X1 i X2 realitzacions independents d'una variable aleatòria X. Aleshores es diu que X és estable si per a qualsevol constant a > 0 i b > 0 la variable aleatòria aX1 + bX2 té la mateixa distribució que cX + d per a algunes constants c > 0 i d. Es diu que la distribució és estrictament estable si això es compleix amb d = 0.

Com que la distribució normal, la distribució de Cauchy i la distribució de Lévy tenen totes la propietat anterior, es dedueix que són casos especials de distribucions estables.

Aquestes distribucions formen una família de quatre paràmetres de distribucions de probabilitat contínues parametritzades pels paràmetres de localització i escala μ i c, respectivament, i dos paràmetres de forma $\beta$ i $\alpha$, corresponent aproximadament a mesures d'asimetria i concentració, respectivament (vegeu les figures).

La funció característica $\varphi (t)$ de qualsevol distribució de probabilitat és la transformada de Fourier de la seva funció de densitat de probabilitat $f(x)$ . La funció de densitat és, per tant, la transformada de Fourier inversa de la funció característica:

$$f(x)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\varphi (t)e^{-ixt}\,dt.$$