Funció de distribució


En teoria de la probabilitat i estadística, la funció de distribució (també funció de distribució acumulada, o CDF pel seu acrònim en anglès cumulative distribution function) d'una variable aleatòria real, avaluada en , és la probabilitat que prengui un valor inferior o igual a . La funció de distribució determina totes les probabilitats relatives a la variable aleatòria. Les funcions de distribució són importants perquè són funcions ordinàries, en contrast amb les probabilitats, que són funcions de conjunts, i llavors les eines de l'Anàlisi matemàtica clàssica poden aplicar-se a estudiar les probabilitats corresponents a les variables aleatòries.
En el cas de les distribucions absolutament contínues, la funció de distribució en el punt és igual a l'àrea sota la funció de densitat de probabilitat de menys infinit a . Les funcions de distribució multidimensionals o multivariants serveixen per especificar les probabilitats dels vectors aleatoris o variables aleatòries multivariades.
Definició[modifica]
Considerem un espai de probabilitat .
|
Observació. Alguns autors[2] defineixen la funció de distribució canviant a l'expressió (*) el menor o igual per un menor estricte: . El conveni que hem adoptat és el més habitual actualment. Cal tenir-ho present, ja que l'ús correcte de les taules de les variables discretes com les de la distribució binomial o la de Poisson depèn d'aquest conveni. És més, fórmules importants com la fórmula d'inversió de Paul Lévy per a la funció característica també es basen en aquesta formulació.
Si es tracta amb diverses variables aleatòries , , etc. aleshores s'escriu , , etc. per indicar les funcions de distribució respectives. El conveni marca l'ús de la majúscula per a la funció de distribució, en contrast amb la minúscula usada per a les funcions de densitat de probabilitat (cas absolutament continu) i les funcions de probabilitat o de repartiment de massa de probabilitat (cas discret). Això s'aplica quan es treballa amb distribucions generals: algunes distribucions específiques tenen la seva pròpia notació, com és el cas de la distribució normal, on la funció de distribució d'una variable normal estàndard s'acostuma a designar per

Propietats[modifica]
Totes aquestes propietats es troben demostrades, per exemple, a[3]
- 1. és una funció monòtona no decreixent (també es diu creixent): si aleshores .
- 2. és contínua per la dreta.
- 3.
Observacions
- (a) Aquestes tres propietats són importants perquè caracteritzen les funcions de distribució de les variables aleatòries: Donada una funció que compleixi aquestes tres propietats, llavors és la funció de distribució d'una variable aleatòria, és a dir, es pot construir un espai de probabilitat i definir-hi una variable aleatòria que tingui aquesta funció com a funció de distribució.
- (b) Quan la funció de distribució es defineix per , aleshores la funció és contínua per l'esquerra.[2]
- 4. Com que és monòtona, en tot punt existeix el límit per l'esquerra[4]. El límit per l'esquerra en el punt el designarem per :
- 5. Probabilitat que pertanyi a diversos tipus d'intervals:
- (a)
- (b)
on és el límit per l'esquerra de en el punt .
- (c)
és a dir, té una discontinuïtat al punt si només si .
- (d)
- (e)
- (d)
- 6. La funció té, com màxim, un nombre numerable de punts de discontinuïtat.
Funcions de distribució de variables discretes, absolutament contínues i mixtes[modifica]
Funció de distribució d'una variable discreta[modifica]
Si X és una variable aleatòria discreta, que pren valors amb probabilitats (funció de probabilitat), llavors la funció de distribució de X serà discontínua en els punts xi i
- Es diu que és una funció de distribució discreta,[5] o una funció de salts o purament discontínua.
Exemple.
Suposem que llencem dues monedes a l'aire. Indiquem una cara amb c i una creu amb s. Els possibles resultats de l'experiment són observar dues cares (cc), una cara seguida d'una creu (cs), una creu seguida d'una cara (sc) i dues creus (ss). Així,
Sigui X la variable aleatòria que compta el nombre de cares obtingudes en el llançament. És a dir, X és la següent funció:
donada per
És una variable discreta, ja que només pot prendre els valors 0, 1 i 2.

La funció de probabilitat és . Vegeu la Figura 4.
La funció de distribució ve donada per
.
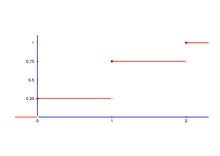
Vegeu la Figura 5.
Observació. A l'exemple anterior, així com en els casos més habituals, com la distribució binomial o la de Poisson, la funció de distribució és esglaonada, però en general no és així. El següent exemple és de Loeve:[6] sigui una ordenació dels nombres racionals, i sigui una variable aleatòria tal que Aleshores la corresponent funció de distribució no és esglaonada; de fet, ni tan sols es pot dibuixar. (Recordeu que , on és la funció zeta de Riemann[7].)
Funció de distribució d'una variable absolutament contínua[modifica]
Recordem que una variable aleatòria es diu que és absolutament contínua o que té densitat (també que és contínua), si existeix una funció que compleix
- 1.
- 2. és integrable i és a dir, l'àrea total entre la gràfica de la funció de densitat i l'eix d'abscisses és 1. Vegeu la Figura 6.

Figura 6. L'àrea entre la corba de la funció de densitat i l'eix d'abscisses és 1.
- 3. Per a ,
És a dir, la probabilitat que la variable prengui un valor de l'interval és l'àrea de la zona limitada pel gràfic de la funció, l'eix de les x i l les rectes x=a i x=b.Vegeu la Figura 7.

Llavors, Vegeu a la Figura 1 quatre funcions de distribució de variables normals i a la Figura 2 les corresponents funcions de densitat.
Funció de distribució d'una variable aleatòria de tipus mixt[modifica]

Hi ha variables aleatòries que són una combinació dels dos tipus anteriors. Per exemple, considerem un mecanisme aleatori com el de la Figura 8: si l'agulla va a parar a la zona de l'esquerra (àrea grisa) aleshores s'obté un 0; si va a parar a la zona de la dreta, aleshores s'obté un nombre decimal entre 0 i 1 amb distribució uniforme. Anomenen el resultat, que és una variable aleatòria que pot prendre un nombre no numerable de valors, i per tant no és discreta, però d'altra banda , i tampoc és contínua. La funció de distribució valdrà:

Vegeu la Figura 9.
Més exemples[modifica]
Suposem que és una distribució uniforme en l'interval unitat [0, 1]. Llavors la seva funció de distribució serà:
Suposem ara que pren només els valors discrets 0 i 1, amb igual probabilitat, és a dir una distribució de Bernoulli amb probabilitat d'èxit de 0.5. Llavors la funció de distribució de vindrà donada per:
Descomposició de funcions de distribució[modifica]
En aquesta secció estudiarem l'estructura de les funcions de distribució, però partint directament d'aquestes funcions, és a dir, de les funcions que compleixen les propietats 1,2 i 3 de la secció Propietats, i recuperarem, des d'un punt de vista més general, allò que hem estudiat a la secció Funcions de distribució de variables discretes, absolutament contínues i mixtes.
Primera descomposició[modifica]
Tal com hem comentat, una funció de distribució només té un nombre finit o infinit numerable de punts de discontinuïtat; sigui , amb el conjunt de punts de discontinuïtat de la funció de distribució , i designem per el salt de la funció en el punt : Definim
La funció compleix les propietats 1,2 i 3 de la definició de funcions de distribució, excepte que Quan aleshores es diu que la funció de distribució és discreta; concretament,
|
Quan direm que és una funció de distribució defectiva (o impròpia).
Definim araLlavors també és una funció de distribució, defectiva, si . Però, a més, com que hem eliminat totes les discontinuïtats de , tenim que és contínua: en tot punt ,
Propietat. Tota funció de distribució es descompon de forma única en suma de dues funcions de distribució (potser defectives), on és contínua i una funció discreta.
Podem normalitzar les funcions i per tal d'obtenir una descomposició amb funcions de distribució: Suposem que Definim que són ambdues funcions de distribució. Quan llavors prenem , i quan llavors prenem .
|
Funcions de distribució singulars[modifica]
Considerem una funció monòtona creixent. Aleshores un conegut teorema de Lebesgue[10] afirma que es pot derivar en quasi tots els punts (Lebesgue), la funció derivada és mesurable (Lebesgue) i per qualsevol , on a l'integral és una integral de Lebesgue.
Llavors, una funció de distribució té derivada en quasi tots punts.
|
Observació. Qualsevol funció de distribució esglaonada (per exemple, la d'una variable binomial o Poisson) és singular. El que és interessant és que existeixen distribucions contínues singulars: per exemple, la distribució de Cantor construïda a partir de la funció de Cantor té una funció de distribució que és contínua, però la seva derivada és zero quasi en tots els punts. Es tracta d'una funció de distribució singular.
Funcions de distribució absolutament contínues[modifica]
Recordem que una funció es diu que és absolutament contínua[11] si donat qualsevol existeix tal que per qualsevol família finita d'intervals oberts disjunts dos a dos tals que es té que Les funcions de distribució que compleixen la propietat anterior es poden identificar amb les integrals indefinides de Lebesgue. Concretament tenim
|
Evidentment, aquest teorema també val per funcions de distribució defectives.
Segona descomposició[modifica]
Continuant amb les notacions de la primera descomposició, suposem que la part contínua no és nul·la: i considerem la seva derivada . Definim la component absolutament contínua de per Finalment, definim la component singular per Cal notar que és contínua singular. Ajuntant-ho amb la primera descomposició tenim:
Propietat. Tota funció de distribució es descompon de forma única en suma de tres funcions de distribució (potser defectives),on és una funció discreta, absolutament contínua i és contínua singular.
Igual que hem fet amb la primera descomposició, si suposem i podem definir i llavors tenim on Fem uns convenis anàlegs als de la primera descomposició quan i són 0 o 1. Tenim:
|
Llavors:
- Si (i naturalment els altres paràmetres 0) llavors és una funció de distribució discreta.
- Si llavors és una funció de distribució contínua.
- - Si llavors és una funció de distribució absolutament contínua.
- - Si llavors és una funció de distribució singular contínua.
Exemple. Considerem de nou l'exemple que hem vist de la variable aleatòria de tipus mixt. La seva funció de distribució és (vegeu la Figura 9). Aquesta funció té una discontinuïtat en el punt 0, amb un salt d'altura 1/2. Llavors,
Notem que es tracta d'una funció de distribució defectiva ja que . La part absolutament contínua és definida per la densitat (defectiva, ja que la seva integral sobre tot no és 1)Normalitzant aquestes funcions defectives tenim on i té funció de densitat
Així, Interpretació probabilística de la descomposició. La funció de distribució discreta correspon a una variable aleatòria degenerada en el zero. La funció correspon a una variable uniforme en l'interval . Sigui una variable aleatòria uniforme en l'interval i sigui una variable aleatòria que utilitzarem per triar a l'atzar entre 0 i , independent d' ; concretament, sigui de Bernoulli de paràmetre p=1/2, independent de : Aleshores la variable aleatòria té funció de distribució .
Interpretació probabilística de la descomposició en el cas general[modifica]
Considerem una funció de distribució que es descompon de la forma amb (recordem que ). Siguin i tres variables independents, (respectivament i ) amb funció de distribució (resp. i ), i una altra variable aleatòria independent de les anteriors, tal que Aleshores la variable aleatòria
té funció de distribució .[15]
Funcions construïdes a partir de la funció de distribució[modifica]
Funció de distribució acumulada complementària (distribució cua)[modifica]
Sovint, és útil estudiar la qüestió oposada i preguntar-se amb quina probabilitat la variable aleatòria està per sobre un nivell en particular. Això s'anomena funció de distribució complementària o simplement distribució cua o excedència, i es defineix com:
Això té aplicacions en contrast d'hipòtesis estadístiques, per exemple, perquè el valor p d'un costat és la probabilitat d'observar un estadístic test com a mínim tan extrem com l'observat. Llavors, sempre que l'estadístic, T, té una distribució contínua, el valor p d'un costat ve simplement donat per la funció de distribució complementària: per un valor t observat en l'estadístic test:
En anàlisi de supervivència, s'anomena la funció de supervivència i es denota , mentre que el terme funció de fiabilitat és habitual en enginyeria.
- Propietats
- Per una variable aleatòria contínua no negativa amb una certa esperança, la desigualtat de Markov diu que[16]
- Com que quan , i de fet sempre que sigui finit.
- Demostració: assumeixi's que la variable aleatòria X té una funció de densitat f, per tot
- Llavors, reconeixent i reordenant els termes queda:
- tal com s'havia dit.
Distribució acumulada plegada[modifica]

Mentre la gràfica d'una distribució acumulada sovint té una forma de S, una il·lustració alternativa és la distribució acumulada plegada o gràfica muntanya, que plega la meitat superior cap a baix,[17][18] que utilitza dues escales, una pel tram inferior i una pel superior. Aquesta forma emfasitza la mediana i la dispersió (específicament, la desviació mitjana respecte la mediana[19]) de la distribució o dels resultats empírics.
Funció de distribució inversa (funció quantil)[modifica]
Si la CDF F és estrictament creixent i contínua, llavors és l'únic nombre real tal que . En aquest cas, això defineix la funció de distribució inversa o la funció quantil.
Algunes distribucions no tenen una única funció inversa (per exemple en el cas en què per tot , fent que sigui constant). Aquest problema es pot solucionar definint, per , la funció de distribució inversa generalitzada:
- Exemple 1: la mediana és .
- Exemple 2: Sigui . S'anomena el 95è percentil.
Algunes propietats útils de la cdf inversa (que també es preserven en la definició de la funció de distribució inversa generalitzada) són:
- és creixent
- si i només si
- If té una distribució llavors és distribuïda com . Això s'usa en generació de nombres aleatoris usant el mètode de mostreig de la transformada inversa.
- Si és una col·lecció de variables aleatòries independents distribuïdes segons definides en el mateix espai de mostreig, llavors existeixen variables aleatòries tals que es distribueixen segons i que amb probabilitat 1 per tot .
Es pot usar la inversa de la cdf per traduir els resultat obtinguts per a la distribució uniforme a altres distribucions.
Cas multivariable[modifica]
Quan es treballa simultàniament amb més d'una variable aleatòria, també es pot definir la funció de distribució acumulada conjunta. Per exemple, per una parella de variables aleatòries X,Y, la CDF conjunta ve donada per:
on la part dreta de l'equació representa la probabilitat que la variable aleatòria X prengui un valor inferior o igual a x i que Y prengui un valor inferior o igual a y.
Més generalment, la funció de distribució d'un vector aleatori[20] és la funció definida per on, com és habitual amb els vectors aleatoris, les comes s'interpreten com interseccions: Té les següents propietats:
- 1. Per a qualsevol parell tenim que
on Noteu que per a , la propietat diu que si , és a dir, que , que és la propietat que havíem vist al cas de dimensió 1.
- 2. És contínua per la dreta: per qualsevol
- 3. i
Ús en anàlisi estadística[modifica]
El concepte de funció de distribució acumulada apareix explícitament en anàlisis estadístiques de dues maneres similars. L'anàlisi de freqüències acumulades és l'anàlisi de la freqüència d'ocurrència de valors d'un fenomen menor que un valor de referència. La funció de distribució empírica és una estimació directa formal de la funció de distribució acumulada de la qual es poden derivar propietats estadístiques simples i que poden ser la base de diversos contrastos d'hipòtesi. Aquests testos serveixen per establir si hi ha proves que una certa mostra de dades ha sorgit d'una determinada distribució, o que dues determinades mostres de dades han sorgit de la mateixa distribució de població desconeguda.
Proves de Kolmogorov–Smirnov i Kuiper[modifica]
La prova de Kolmogórov-Smirnov es base en les funcions de distribució acumulades i es poden usar per veure si dues distribucions empíriques són diferents o si una distribució empírica és diferent d'una distribució ideal. La prova de Kuiper és útil si el domini de la distribució és cíclic com els dies de la setmana. Per exemple, es pot usar la prova de Kuiper per veure si el nombre de tornados varia durant l'any o si les vendes d'un producte varien segons el dia de la setmana o segons el dia del mes.
Bibliografia[modifica]
- Athreya, Krishna B. Measure theory and probability theory. Nova York: Springer, 2006. ISBN 0-387-32903-X.
- Chung, Kai Lai. A course in probability theory. 3a edició. San Diego: Academic Press, 2001. ISBN 978-0-08-052298-2.
- Loeve, Michel. Teoría de la probabilidad. Madrid: Tecnos, 1976. ISBN 84-309-0663-0.
- Olver, F.W.J. [et al.].. NIST handbook of mathematical functions. Cambridge: Cambridge University Press, 2010. ISBN 978-0-521-19225-5.
- Royden, H. L.. Real analysis. 3a edició. Nova York: Macmillan, 1988. ISBN 0-02-404151-3.
- Sanz, Marta. Probabilitats. Barcelona: Edicions Universitat de Barcelona, 1999. ISBN 84-8338-091-9.
Notes[modifica]
- ↑ Sanz, 1999, p. 42.
- ↑ 2,0 2,1 Loeve, 1976, p. 167.
- ↑ Sanz, 1999, p. 43-47.
- ↑ Chung, 2001, p. 2.
- ↑ Chung, 2001, p. 9.
- ↑ Loeve, 1976, p. 177.
- ↑ Olver, 2010, p. 605, Fórmula 25.6.1.
- ↑ Chung, 2001, p. 10.
- ↑ Athreya, 2006, p. 47.
- ↑ Royden.
- ↑ Billingsley, 1986, p. 433.
- ↑ Billingsley, 1986, p. 434, Theorem 31.8.
- ↑ Chung, 2001, p. 12.
- ↑ Athreya, 2006, p. 134.
- ↑ Athreya, 2006, p. 215.
- ↑ Zwillinger, Daniel; Kokoska, Stephen. CRC Standard Probability and Statistics Tables and Formulae. CRC Press, 2010, p. 49. ISBN 978-1-58488-059-2.
- ↑ Gentle, J.E.. Computational Statistics. Springer, 2009. ISBN 978-0-387-98145-1 [Consulta: 6 agost 2010].
- ↑ Monti, K.L. «Folded Empirical Distribution Function Curves (Mountain Plots)». The American Statistician, 49, 1995, pàg. 342–345. DOI: 10.2307/2684570. JSTOR: 2684570.
- ↑ Xue, J. H.; Titterington, D. M. «The p-folded cumulative distribution function and the mean absolute deviation from the p-quantile». Statistics & Probability Letters, 81, 8, 2011, pàg. 1179–1182. DOI: 10.1016/j.spl.2011.03.014.<
- ↑ Sanz, 1999, p. 66-68.




![{\displaystyle F:\mathbb {R} \longrightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd7f6e4d15edf1cc4d244b20386efcaaa2e87382)
![{\displaystyle F(x)=P(X\leq x)=P{\big (}X\in (-\infty ,x]{\big )}.\qquad (*)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6d725161d59d9a9024438d7608d99ecb842eb6c)












![{\displaystyle P{\big (}X\in (s,t]{\big )}=P(s<X\leq t)=F(t)-F(s).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9b1144208e4ecaf0dde09378f671eebf596e3ce)

























![{\displaystyle [a\,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8eb6adb51b90cab4ec61b26d89c0dd47bd500c92)





























![{\displaystyle c\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02b2796dc5e3cb6527d1ac6e766dc1da2ef1e120)













































![{\displaystyle f(x)={\begin{cases}1,&{\text{si }}x\in [0,1],\\0,&{\text{en cas contrari.}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30477d6a279b8d8e812e68bb68ae9986faf3db23)





































![{\displaystyle F^{-1}(p),p\in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b89fe1b58ff06ad5647ba178886bb6704d8da846)



![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)









![{\displaystyle U[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4a82b2a883d751cf53e5ac11ea12b9e36298f0)







![{\displaystyle F:\mathbb {R} ^{n}\to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27cdc4f881f2e15bfe75becb7d2f1a0e88a94b4c)











