Funció monòtona
En matemàtiques, una funció entre conjunts ordenats es diu monòtona (o isotònica) si conserva l'ordre donat. Les funcions d'aquesta classe van sorgir primerament en càlcul, i van ser després generalitzades a l'entorn més abstracte de la teoria de l'ordre. Encara que els conceptes generalment coincideixen, les dues disciplines han desenvolupat una terminologia lleugerament diferent, mentre en càlcul es parla de funcions monòtonament creixents i monòtonament decreixents (o simplement creixents i decreixents),[1][2] en la teoria de l'ordre es fan servir els termes monòtona i antítona, o es parla de funcions que conserven i inverteixen l'ordre.
Definició general[modifica]
Sigui
una funció entre dos conjunts P i Q , on cada conjunt té un ordre parcial (els dos es denotarà per ≤). En anàlisi matemàtica es parla de funcions entre subconjunts dels reals, i l'ordre ≤ no és altre que l'ordre usual de la recta real, encara que això no és essencial per a la definició.
La funció f és monòtona si, sempre que x ≤ i , s'ha f ( x ) ≤ f ( i ). En altres paraules, una funció monòtona és una que conserva l'ordre.[3]
Monòtona en càlcul i anàlisi[modifica]
En càlcul no hi ha usualment necessitat d'invocar els mètodes abstractes de la teoria de l'ordre. Com ja es va assenyalar, les funcions s'estableixen entre (subconjunts de) nombres reals, ordenats de manera natural.
Per la forma de la gràfica d'una funció monòtona en els reals, com funcions s'anomenen també monòtonament creixents (o no decreixent), respectivament.
Exemple gràfic[modifica]
A continuació es mostren tres gràfiques de funcions qualssevol. La primera d'elles és una funció estrictament creixent, ja que conserva l'ordre ascendent durant tot el recorregut de la funció. La segona d'elles és estrictament decreixent, ja que conserva l'ordre descendent durant tot el recorregut de la funció. L'última d'elles és una funció amb un recorregut amb parts on la funció és creixent i parts on és decreixent (presenta màxims i mínims relatius).[4]
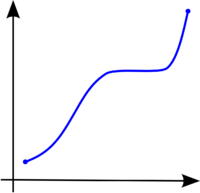 Funció monòtona creixent. |
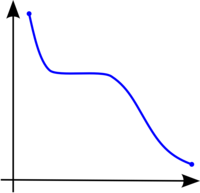 Funció monòtona decreixent. |
 Funció no monòtona. |
Aplicacions i resultats bàsics[modifica]
Monotonia. En matemàtiques, cadascuna de les següents propietats d'una funció f : R → R implica la següent:
- f és monòtona.
- f té un límit per l'esquerra i per la dreta en qualsevol punt del seu domini de definició.
- f només pot tenir discontinuïtats de salt.
- f només pot tenir una quantitat enumerable de discontinuïtats.
Aquestes propietats són la raó per la qual les funcions monòtones són útils en l'anàlisi matemàtica. Dos importants fets que es dedueixen que una funció sigui monòtona són:
- Si f és una funció monòtona definida en un interval I , llavors f és derivable gairebé sempre en I , és a dir, el conjunt de punts x en I on f no és diferenciable té mesura de Lebesgue 0.
- Si f és una funció monòtona definida en un interval [ a , b ], llavors f és Riemann-integrable.
Una important aplicació de les funcions monòtones és en probabilitat. Si X és una variable aleatòria, la seva funció de distribució
és una funció creixent.
Referències[modifica]
- ↑ Maths, Sangaku. «Monotonia: creixement i decreixement». [Consulta: 26 gener 2022].
- ↑ «Resum de continguts sobre funcions». [Consulta: 26 gener 2022].
- ↑ «What does monotonic function mean?». [Consulta: 29 gener 2022].
- ↑ «How to Determine If a Function is Monotonic». [Consulta: 29 gener 2022].


