Programació quadràtica

Esquema de programació quadràtica seqüencial Esquema que explica la idea bàsica de l'algorisme SQP creat per a l'article de wikipedia SQP amb TikZ.

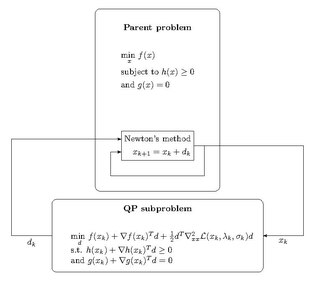
La programació quadràtica (QP) és el procés de resolució de determinats problemes d'optimització matemàtica que impliquen funcions quadràtiques. Concretament, es busca optimitzar (minimitzar o maximitzar) una funció quadràtica multivariant subjecta a restriccions lineals sobre les variables. La programació quadràtica és un tipus de programació no lineal.

"Programació" en aquest context es refereix a un procediment formal per resoldre problemes matemàtics. Aquest ús data de la dècada de 1940 i no està específicament lligat a la noció més recent de "programació d'ordinadors". Per evitar confusions, alguns professionals prefereixen el terme "optimització", per exemple, "optimització quadrada".

Formulació del problema

El problema de programació quadràtica amb n variables i m restriccions es pot formular de la següent manera. Donat:

• un vector n -dimensional de valor real c,
• una matriu simètrica real n×n-dimensional Q,
• una matriu real m×n -dimensional A, i
• un vector real m -dimensional b,

l'objectiu de la programació quadràtica és trobar un vector n -dimensional x, que ho farà

minimitzar	${\tfrac {1}{2}}\mathbf {x} ^{\mathrm {T} }Q\mathbf {x} +\mathbf {c} ^{\mathrm {T} }\mathbf {x}$
subjecte a	$A\mathbf {x} \preceq \mathbf {b} ,$

on x^T denota la transposició vectorial de x, i la notació Ax ⪯ b significa que cada entrada del vector Ax és menor o igual que l'entrada corresponent del vector b (desigualtat per components).

Mínims quadrats restringits

Com a cas especial quan Q és simètrica positiva-definida, la funció de cost es redueix a mínims quadrats:

minimitzar	${\tfrac {1}{2}}\|R\mathbf {x} -\mathbf {d} \|^{2}$
subjecte a	$A\mathbf {x} \preceq \mathbf {b} ,$

on Q = R^TR es desprèn de la descomposició de Cholesky de Q i c = −R^T d. Per contra, qualsevol programa de mínims quadrats restringit es pot emmarcar de manera equivalent com un problema de programació quadràtica, fins i tot per a una matriu R genèrica no quadrada.

Generalitzacions

Quan es minimitza una funció f al voltant d'algun punt de referència x₀, Q s'estableix a la seva matriu hessiana H(f(x₀)) i c s'estableix al seu gradient ∇f(x₀). Un problema de programació relacionat, la programació quadràtica restringida, es pot plantejar afegint restriccions quadràtiques a les variables.

Mètodes de solució

Per a problemes generals s'utilitzen habitualment una varietat de mètodes, com ara

• punt interior,
• conjunt actiu,
• Lagrangià augmentat,
• gradient conjugat,
• projecció de gradient,
• extensions de l'algorisme simplex.

En el cas en què Q és definit positiu, el problema és un cas especial del camp més general de l'optimització convexa.