Usuari:Jordiventura96/proves/Algorisme de Kruskal

Aquesta és una pàgina de proves de Jordiventura96. Es troba en subpàgines de la mateixa pàgina d'usuari. Serveix per a fer proves o desar provisionalment pàgines que estan sent desenvolupades per l'usuari. No és un article enciclopèdic. També podeu crear la vostra pàgina de proves.

Vegeu Viquipèdia:Sobre les proves per a més informació, i altres subpàgines d'aquest usuari

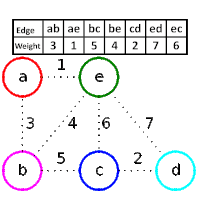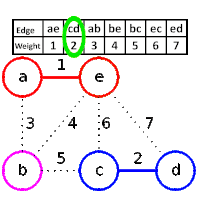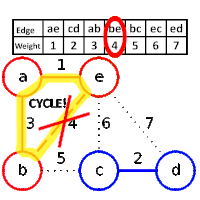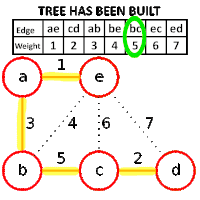
En teoria de grafs, l'algorisme de Kruskal és un algorisme que serveix per trobar l'arbre generador amb el menor pes que connecta tots els punts d'un graf.^[1] Es tracta d'un algorisme voraç ja que troba l'arbre generador mínim per un graf ponderat connex afegint arcs de pes superior en cada pas.^[1] Això significa que troba un subconjunt d'arestes que formen un arbre que inclou cada vèrtex, tal que el pes total de les arestes és el mínim. Si el graf no és connex troba un bosc generador mínim (un arbre generador mínim per a cada component connex).

Aquest algorisme va aparèixer per primer cop a Proceedings of the American Mathematical Society, pp. 48–50 el 1956 i va ser escrit per Joseph Kruskal.^[2]

Altres algorismes per aquest problema poden ser l'algorisme de Prim, l'algorisme d'eliminació cap enrere o l'algorisme de Borůvka.

Descripció

Els passos que s'han de seguir en l'execució de l'algorisme de Kruskal sónː

Crear un bosc F (un conjunt d'arbres), en què cada vèrtex del graf és un arbre
Crear un conjunt S que contingui totes les arestes del graf
mentre S no sigui buit i F encara no sigui un arbre d'expansió
- treure l'aresta de mínim pes de S
- si l'aresta extreta conecta dos arbres diferents, llavors afegir-la al bosc F, combinant els dos arbres en un de sol

Exemple

Imatge	Descripció
	AD i CE són les arestes més curtes, amb longitud 5, i AD s'ha elegit arbitràriament, i és per tant subratllat en verd.
	CE és ara l'aresta més curta que no forma un cicle amb AD, amb longitud 5, així que és subratllat com a segona aresta.
	La següent aresta, DF amb longitud 6, és subratllada en la següent iteració.
	Les arestes de mínima longitud següents són AB i BE, ambdues amb longitud 7. AB es tria arbitràriament, i és subratllat. L'aresta BD s'ha subratllat en vermell, perquè ja existeix un camí (en verd) entrre B i D, així que, de ser afegit, formaria un cicle (ABD).
	El procés continua subratllant la següent aresta més petita, BE amb longitud 7. Més arestes són subratllades en vermell en aquest pas: BC perquè formaria el bucle BCE, DE perquè formaria el bucle DEBA, i FE perquè formaria FEBAD.
	Finalment, el procés acaba amb l'aresta EG de longitud 9, i ja s'ha trobat l'arbre generador mínim.

Vegeu també

Referències

↑ ^1,0 ^1,1 Cormen, Thomas; Charles E Leiserson, Ronald L Rivest, Clifford Stein. Introduction To Algorithms. Third. MIT Press, 2009, p. 631. ISBN 0262258102.
↑ Kruskal, J. B. «On the shortest spanning subtree of a graph and the traveling salesman problem». Proceedings of the American Mathematical Society, vol. 7, 1956, pàg. 48–50. DOI: 10.1090/S0002-9939-1956-0078686-7. JSTOR: 2033241.

[:0-1] 1,0 ^1,1 Cormen, Thomas; Charles E Leiserson, Ronald L Rivest, Clifford Stein. Introduction To Algorithms. Third. MIT Press, 2009, p. 631. ISBN 0262258102.

[2] Kruskal, J. B. «On the shortest spanning subtree of a graph and the traveling salesman problem». Proceedings of the American Mathematical Society, vol. 7, 1956, pàg. 48–50. DOI: 10.1090/S0002-9939-1956-0078686-7. JSTOR: 2033241.

[1]

[2]