Mòdul de cisallament
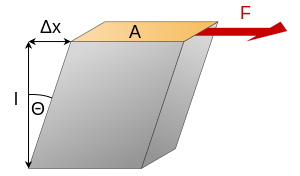 Esquema de l'esforç tallant | |
| Símbol | G |
|---|---|
| Unitats | pascal |
| Derivacions a partir d'altres quantitats | G = τ / γ |
| Fórmula | |
El mòdul de cisallament o rigidesa (també anomenat mòdul d'elasticitat transversal ) és una constant elàstica que caracteritza el canvi de forma que experimenta un material elàstic quan s'apliquen esforços tallants.
Aquest mòdul rep una gran varietat de noms, entre els quals cal destacar els següents: Mòdul de rigidesa, mòdul de tall, mòdul de cortadura, mòdul elàstic tangencial, mòdul d'elasticitat transversal, ...
Per a un material elàstic lineal i isòtrop, el mòdul d'elasticitat transversal té el mateix valor per a totes les direccions de l'espai.
Definició[modifica]
Experimentalment el mòdul elàstic transversal (o mòdul cortitilatante) pot mesurar de diverses maneres, conceptualment la forma més senzilla és considerar un cub com el de la fig. 1 i sotmetre'la una força tallant, per a petites deformacions es pot calcular la raó entre la tensió i la deformació angular:
Materials isòtrops lineals[modifica]
Per a un material isòtrop elàstic lineal el mòdul d'elasticitat transversal està relacionat amb el mòdul de Young i el coeficient de Poisson mitjançant la relació:
On:
- és el mòdul d'elasticitat longitudinal o mòdul de Young.
- és el coeficient de Poisson.
- són respectivament la tensió tangencial i la deformació tangencial sobre el pla format pels eixos X i i X j .
Materials anisòtrops[modifica]
Els materials elàstics lineals anisòtrops es caracteritzen per presentar diferents valors de les constants elàstiques segons la direcció en la qual s'apliquen les forces. En general, en un material anisòtrop en aplicar esforços tangents a una superfície apareixen deformacions normals a aquesta. Això significa que els modes transversals i longitudinals no estan desacoblats i per aquesta raó els conceptes de mòdul d'elasticitat longitudinal i mòdul d'elasticitat transversal no es poden generalitzar adequadament, en tots els casos.
- Materials ortotrópics
Un cas particular de material anisòtrop on sí que es pot parlar de mòduls d'elasticitat longitudinals i transversals són els anomenats materials ortotrópics, la fusta és un exemple de material ortotrópico, sovint usat en construcció.
En els materials ortotrópicos les formes transversals i longitudinals de deformació estan desacoblats. Això permet identificar clarament mòduls d'elasticitat transversal i mòduls d'elasticitat longitudinal. Per a un material ortotrópic general poden definir tres mòduls d'elasticitat longitudinals bàsics ( N x , N i ', E z ) i tres mòduls d'elasticitat transversal ( G xi , G xz ', G yz ). Aquests últims es defineixen com:
Per a un material com la fusta les coordenades X, Y i Z anteriors es prenen de la següent manera:
- L'eix X està alineat amb la direcció longitudinal de la fibra.
- L'eix Y es pren perpendicular als anells de la secció transversal.
- L'eix Z es pren tangent als anells de la secció transversal.
Els mòduls d'elasticitat transversal en aquestes tres direccions són diferents per a la fusta i poden arribar a presentar grans diferències de valor entre elles.
Valors per a diversos materials[modifica]
Per veure el valor del mòdul d'elasticitat transversal per diversos materials consultar els valors del mòdul d'elasticitat transversal de Llista de Constants elàstiques de diferents materials.







