Sistema triclínic

Exemple d'un cristall triclínic

En cristal·lografia, un sistema cristal·logràfic triclínic és un dels set sistemes cristal·lins. Un sistema cristal·logràfic que esta descrit per tres vectors base. En el sistema triclínic, el cristall està descrit per vectors de longitud desigual, tal com en el sistema ortoròmbic. A més, cap d'ells és ortogonal amb algun altre.

Classes

triclínic (a ≠ b ≠ c and α ≠ β ≠ γ)

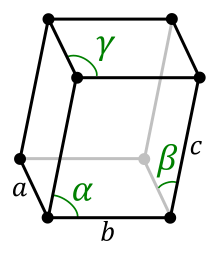
Els cristalls d'aquest sistema es classifiquen en les dues classes següents:

• Pinacoidal (o triclínic normal)
• Pedial (o triclinic hemihedral)

Volum d'una cel·la

El volum d'un paral·lelepípede en que els costats siguin els vectors $\vec{a}$, $\vec{b}$, $\vec{c}$ està donat pel triple producte escalar:

$V =|\vec{c}\cdot \left (\vec{a}\times \vec{b}\right)|$

Per conveniència, posarem el vector $\vec{a}$ sobre l'eix $x$, i el vector $\vec{b}$ sobre el pla $xy$, llavors tindrem els següents vectors:

$\begin{array}{rll} \vec{a} & = \langle a, 0, 0 \rangle & \\ \vec{b} & = \langle b \cos \alpha, b sen \alpha, 0 \rangle & \\ \vec{c} & = \langle c_x, c_y, c_z \rangle & \end{array}$

Per poder fer el triple producte escalar, és necessari conèixer els components de $\vec{c}$. Els podem esbrinar fent els següents productes escalars:

$\vec{a} \cdot \vec{c} = a c_x = a c \cos \beta$

Per tant:

$c_x = c \cos \beta \;$

Enllaços externs

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Sistema triclínic

• Webmineral.com