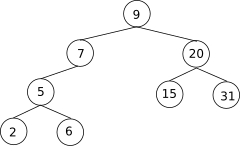
Arbre binari de cerca
En ciències de la computació, un arbre binari de cerca (BST, de l'anglès Binary Search Tree) és un tipus particular d'arbre binari que presenta una estructura de dades en forma d'arbre.
Descripció
[modifica]Un arbre binari de cerca és un arbre binari definit de la següent manera:
|
Dit de manera resumida, és un arbre binari en què el subarbre esquerre de qualsevol node (si no buit) conté valors menors que el que conté aquest node, i el subarbre dret (si no buit) conté valors més grans. Per tant, segons aquesta definició, hi ha una relació d'ordre establerta entre els elements dels nodes. Que certa relació estigui definida, o no, depèn de cada llenguatge de programació. D'aquí es dedueix que hi pot haver diferents arbres binaris de cerca per a un mateix conjunt d'elements.
L'alçada total de l'arbre (h) al pitjor dels casos tindrà la mateixa mida que el nombre d'elements disponibles. I en el millor dels casos ve donada per l'expressió , on indica arrodoniment a l'alça.

L'interès dels arbres binaris de cerca és que el seu recorregut en inorder proporciona els elements ordenats de forma ascendent i que la recerca d'algun element sol ser molt eficient.
Depenent de les necessitats de l'usuari que tracti amb una estructura d'aquest tipus es podrà permetre la igualtat estricta en algun, en cap o en ambdós subarbres que pengen de l'arrel. Permetre l'ús de la igualtat provoca l'aparició de valors dobles i fa la recerca més complexa.
Un arbre binari de cerca no deixa de ser un cas particular d'arbre binari. Amb la següent especificació d'arbre binari en Maude:
fmod TREE-BINARY {X :: TRIV} is
sorts TreeBinNV{X} TreeBin{X} .
subsort TreeBinNV{X} < TreeBin{X} .
*** generadors
op create : -> TreeBin{X}[ctor] .
op treeBin : X$Elt TreeBin{X} TreeBin{X} -> TreeBinNV{X}[ctor] .
endfmpodem fer la següent definició per a un arbre binari de cerca (també en Maude):
fmod TREE-BINARY-SEARCH {X :: ORDER} is
protecting TREE-BINARY{VOrder}{X} .
sorts BST{X} BSTNV{X} .
subsort BSTNV{X} < BST{X} .
subsort BST{X} < TreeBin{VOrder}{X} .
subsort BSTNV{X} < TreeBinNV{VOrder}{X} .
*** generadors
op create : -> TreeBin{X}[ctor] .
op treeBin : X$Elt TreeBin{X} TreeBin{X} -> TreeBinNV{X}[ctor] .
endfmamb la següent teoria d'ordre:
fth ORDER is
Protecting BOOL .
sort ELT .
*** operacions
op _ <_: ELT ELT → Bool .
endfthPerquè un arbre binari pertanyi al tipus arbre binari de cerca ha de complir la condició d'ordenació següent que aniria al costat del mòdul TREE-BINARY-SEARCH:
var R : X$Elt .
vars INV DNV : BSTNV{X} .
vars I D : BST{X} .
mb create : BST{X} .
mb treeBin(R, create, create) : BSTNV{X} .
cmb treeBin(R, INV, create) : BSTNV{X} if R > max(INV) .
cmb treeBin(R, create, DNV) : BSTNV{X} if R < min(DNV) .
cmb treeBin(R, INV, DNV) : BSTNV{X} if (R > max(INV)) and (R < min(DNV)) .
ops min max : BSTNV{X} -> X$Elt .
eq min(treeBin(R, create, D)) = R .
eq min(treeBin(R, INV, D)) = min(INV) .
eq max(treeBin(R, I, create)) = R .
eq max(treeBin(R, I, DNV)) = max(DNV) .Implementació en Python:
class node:
left, right, data = None, None, 0
def __init__(self, data):
# Crea un node
self.left = None
self.right = None
self.data = data
class binaryTree:
def __init__(self):
# Inicia l'arrel
self.root = None
def insertNode(self, data):
# Crea un nou node i el retorna
return node(data)
def insert(self, root, data):
# Inserta un valor nou a l'arbre
if root == None:
# Si no hi ha nodes a l'arbre, l'agrega
return self.insertNode(data)
else:
# Si hi ha nodes a l'arbre, el recorre
if data <= root.data:
# Si el valor és menor que el guardat, va al subarbre esquerre
root.left = self.insert(root.left, data)
else:
# Si no, va al subarbre dret
root.right = self.insert(root.right, data)
return root
Operacions
[modifica]Totes les operacions realitzades sobre arbres binaris de cerca estan basades en la comparació dels elements o clau dels mateixos, per la qual cosa cal una subrutina, que pot estar predefinida en el llenguatge de programació, que els compari i pugui establir una relació d'ordre entre ells, és a dir, que donats dos elements sigui capaç de reconèixer quina és major i quina menor. Es parla de clau d'un element perquè en la majoria dels casos el contingut dels nodes serà un altre tipus d'estructura i cal que la comparació es faci sobre algun camp al que s'anomena clau.
Cerca
[modifica]La cerca a l'arbre consisteix en accedir a l'arrel; si l'element a localitzar coincideix amb aquest llavors la cerca es dona per conclosa, si l'element és menor es busca en el subarbre esquerre i si és major en el dret. Si s'arriba a un node fulla i l'element no ha estat trobat, se suposa que no existeix en l'arbre. Cal destacar que la cerca en aquest tipus d'arbres és molt eficient, representa una funció logarítmica. El màxim nombre de comparacions que necessitaríem per saber si un element es troba en un arbre binari de cerca estaria entre log₂(n+1) i n, essent n el nombre de nodes. La recerca d'un element en un arbre binari de cerca es pot realitzar de dues formes; iterativa o recursiva.
Exemple de versió iterativa al llenguatge de programació C, suposant que estem buscant una clau allotjada en un node on hi ha el corresponent "dada" que necessitem trobar:
data search_BST(abb t, key k) {
abb p;
data e;
e=NULL;
p=t;
if (!isNull(p)) {
while (!isNull(p) && (p->k!=k)) {
if (k < p->k) p = p->l;
if (p->k < k) p = p->r;
}
if (!isNull(p) &&(p->d!=NULL)) {
e = copyData(p->d);
}
}
return e;
}
Vegeu ara la versió recursiva en aquest mateix llenguatge:
int search(tTree *a, int elem) {
if (a == NULL) {
return 0;
} else if (a->key < elem) {
return search(a->hRight, elem);
} else if (a->key > elem) {
return search(a->hLeft, elem);
} else {
return 1;
}
}
Un altre exemple, en Python:
def search_binary_tree(node, key):
if node is None:
return None # No s'ha trobat
if key < node.key:
return search_binary_tree(node.left, key)
else if key > node.key:
return search_binary_tree(node.right, key)
else:
return node.value
En Pascal:
Function search(T: ABR, y: integer): ABR
begin
if (T=nil) or (^T.root=y) then
search:=T;
else
if (^T.root<y) then
search:=search(^T.right,y);
else
search:=search(^T.left,y);
end;
Una especificació en Maude per a l'operació de cerca quedaria de la següent manera:
op this? : X$Elt ABB{X} -> Bool .
var R R1 R2 : X$Elt .
vars I D : ABB{X} .
eq this?(R, create) = false .
eq this?(R1, treeBin(R2, I, D)) =
if R1 == R2 then
true
else
if R1 < R2 then
this?(R1, I)
else
this?(R1, D)
end
end .Inserció
[modifica]La inserció és similar a la cerca, es pot donar una solució tant iterativa com recursiva. Si tenim inicialment com a paràmetre un arbre buit, es crea un nou node com a únic contingut l'element a inserir. Si no ho està, es comprova si l'element donat és menor que l'arrel de l'arbre inicial amb el que s'insereix en el subarbre esquerre, i si és major s'insereix en el subarbre dret. D'aquesta manera, les insercions es fan a les fulles.

Com en el cas de la cerca pot haver diverses variants a l'hora d'implementar la inserció en el ADT (de l'anglès, Abstract Data Type), i és la decisió a prendre quan l'element (o clau de l'element) a inserir ja es troba en l'arbre; pot ser que aquest sigui modificat o que sigui ignorada la inserció. Aquesta operació modifica l'arbre, perdent la versió anterior d'aquest.
A continuació hi ha les dues versions de l'algorisme amb pseudocodi, iterativa i recursiva, respectivament.
PROC InsertarSBT (arbre: Tabba; dada: TElement) VARIABLES nou_node, PAV, pret: Tabba nova_clau: Tclau elements: TElement INICI nou_node <- NOU (TNodeSBT) nou_node^. esquerra <- NUL nou_node^. dreta <- NUL nou_node^. elem <- dada SI SBTBuit(arbre) LLAVORS arbre <- nou_node EN_CAS_CONTRARI nova_clau <- dada.clau PAV <- arbre // Punter Avançat pret <- NUL // Punter retardat MENTRE (PAV <- NUL) FER pret <- PAV elements = PAV^. elem SI (nova_clau < ele.clau) LLAVORS PAV <- PAV^. esquerra EN_CAS_CONTRARI PAV <- PAV^. dreta FI_SI FI_MENTRE elements = pret^. elem SI (nova_clau < ele.clau) LLAVORS pret^. esquerra <- nou_node EN_CAS_CONTRARI pret^. dreta <- nou_node FI_SI FI_SI FI
PROC InsertarSBT (arbre: Tabba; dada: TElement) VARIABLES elements: TElement INICI SI (SBTBuit(arbre)) LLAVORS arbre <- NOU (TNodeSBT) arbre^. esquerra <- NUL arbre^. dreta <- NUL arbre^. elem <- dada EN_CAS_CONTRARI elements = InfoSBT (arbre) SI (dada.clau < ele.clau) LLAVORS InsertarSBT (arbre^. esquerra, dada) EN_CAS_CONTRARI InsertarSBT (arbre^. dreta, dada) FI_SI FI_SI FI
Es pot apreciar la simplicitat que ofereix la versió recursiva; aquest algorisme és la traducció en C. L'arbre és passat per referència perquè els nous enllaços als subarbre mantinguin la coherència.
void insert(tTree **a, int elem) {
if (*a == NULL) {
*a = (tTree *) malloc(sizeof(tTree));
(*a)->key = elem;
(*a)->hLeft = NULL;
(*a)->hRight = NULL;
} else if ((*a)->key < elem) {
insert(&(*a)->hRight, elem);
} else if ((*a)->key > elem) {
insertar(&(*a)->hLeft, elem);
}
}
Exemple en Python:
def binary_tree_insert(node, key, value):
if node is None:
return TreeNode(None, key, value, None)
if key == node.key:
return TreeNode(node.left, key, value, node.right)
if key <node.key:
return TreeNode(binary_tree_insert(node.left, key, value), node.key, node.value, node.right)
else:
return TreeNode(node.left, node.key, node.value, binary_tree_insert(node.right, key, value))
Un altre exemple en Pascal:
Procedure Insertion(var T:ABR, y:integer)
var
last_node:ABR;
current_node:ABR;
new_node:ABR;
begin
last_node:=nil;
current_node:=T;
while (current_node<>nil) do
begin
last_node:=current_node;
if (current_node^.root<y) then
current_node:=current_node^.right
else
current_node:=current_node^.left;
end;
new(new_node);
^new_node.root:=y;
^new_node.left:=nil;
^new_node.right:=nil;
if last_node=nil then
T:=new_node
else
if last_node^.root<y then
last_node^.right:=new_node
else
last_node^.left:=new_node;
end;
Vegeu també un exemple d'algorisme recursiu d'inserció en un BST en el llenguatge de programació Maude:
op insert : X$Elt BST{X} -> BSTNV{X} .
var R R1 R2 : X$Elt .
vars I D : BST{X} .
eq insert(R, create) = treeBin(R, create, create) .
eq insert(R1, treeBin(B2, I, D)) =
if R1 < R2 then
treeBin(R2, insert(R1, I), D)
else
treeBin(R2, I, insert(R1, D))
end .L'operació d'inserció requereix, en el pitjor dels casos, un temps proporcional a l'altura de l'arbre.
Esborrat
[modifica]L'operació d'esborrat no és tan senzilla com les de recerca i inserció. Hi ha diversos casos a tenir en consideració:[1]
- Esborrar un node sense fills o node fulla : simplement s'esborra i s'estableix a nul l'apuntador del seu predecessor.
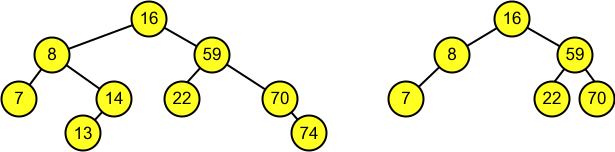
- Esborrar un node amb un subarbre fill : s'esborra el node i s'assigna el seu subarbre fill com subarbre del seu predecessor.

- Esborrar un node amb dos subarbres fill : la solució està en reemplaçar el valor del node pel del seu predecessor o pel del seu successor en inorder i posteriorment esborrar aquest node. El seu predecessor en inorder serà el node més a la dreta del seu subarbre esquerre (major node del subarbre esquerre), i el seu successor el node més a l'esquerra del seu subarbre dret (menor node del subarbre dret). En la següent figura es mostra com existeix la possibilitat de realitzar qualsevol dels dos reemplaçaments:
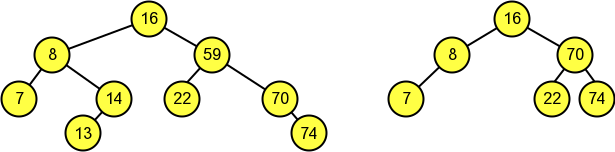
El següent algorisme en C realitza l'esborrament en un BST. El procediment replace busca la major clau del subarbre esquerre i l'assigna al node a eliminar.
void replace(tTree **a, tTree **aux); /*Prototip de la funció replace */
void remove(tTree **a, int elem) {
tTree *aux;
if (*a == NULL) return;
if ((*a)->key < elem)
remove(&(*a)->hRight, elem);
else if ((*a)->key > elem)
remove(&(*a)->hLeft, elem);
else if ((*a)->key == elem)
{
aux = *a;
if ((*a)->hLeft== NULL)
*a = (*a)->hRight;
else if ((*a)->hRight== NULL)
*a = (*a)->hLeft;
else
replace(&(*a)->hLeft, &aux);
free(aux);
}
}
void replace(tTree **a, tTree **aux) {
if ((*a)->hRight == NULL) {
(*aux)->key = (*a)->key;
*aux = *a;
*a = (*a)->hLeft;
} else
replace(&(*a)->hRight, aux);
}
Un altre exemple en Pascal.
Procedure Remove(var T:ABR, x:ABR)
var
aRemove:ABR;
previous:ABR;
current:ABR;
descendent:ABR;
begin
if (^x.left=nil) or (^x.right=nil) then
aRemove:=x;
else
aRemove:=successor(T,x);
current:=T;
previous:=nil;
while (current<>aRemove) do
begin
previous:=current;
if (^current.root<^aRemove.root) then
current:=^current.right;
else
current:=^current.left;
end;
if (^current.left=nil) then
descendent:=^current.right;
else
descendent:=^current.left;
if (previous=nil) then
T:=descendent;
else
if (^previous.root<^current.root) then
^previous.right:=descendent;
else
^previous.left:=descendent;
if (aRemove<>x) then
^x.root:=^aRemove.root;
free(aRemove);
end;
Vegeu també un exemple d'algorisme recursiu de supressió en un BST en el llenguatge de programació Maude, considerant els generadors create i treeBin. Aquesta especificació fa ús de la component clau a partir de la qual s'ordena l'arbre.
op delete : X$Elt BST{X} -> BST{X} .
vars R M : X$Elt .
vars I D : ABB{X} .
vars INV DNV : ABBNV{X} .
ops max min : TreeBin{X} -> X$Elt .
eq min(treeBin(R, create, D)) = R .
eq max(treeBin(R, I, create)) = R .
eq min(treeBin(R, INV, D)) = min(INV) .
eq max(treeBin(R, I, DNV)) = max(DNV) .
eq delete(M, create) = create .
ceq delete(M, treeBin(R, create, D)) = D if M == key(R) .
ceq delete(M, treeBin(R, I, create)) = I if M == key(R) .
ceq delete(M, treeBin(R, INV, DNV)) = treeBin(max(INV), delete(key(max(INV)), INV), DNV) if M == key(R) .
ceq delete(M, treeBin(R, I, D)) = treeBin(R, delete(M, I), D) if M < key(R) .
ceq delete(M, treeBin(R, I, D)) = treeBin(R, I, delete(M, D)) if key(R) < M .Altres Operacions
[modifica]Una altra opereció seria per exemple comprovar que un arbre binari és un arbre binari de cerca. La seva implementació en Maude és la següent:
op isBST? : BST{X} -> Bool .
var R : X$Elt .
vars I D : BST{X} .
eq isBST?(create) = true .
eq isBST?(treeBin(R, I, D)) = (Max(I) < R) and (Min(D) > R) and (isBST?(I)) and (isBST?(D)) .Recorreguts
[modifica]Es pot fer un recorregut d'un arbre en profunditat o en amplada.
Els recorreguts en amplada són per nivells, es realitza horitzontalment des de l'arrel a tots els fills abans de passar a la descendència d'algun dels fills.
El recorregut en profunditat porta al camí des de l'arrel cap al descendent més llunyà del primer fill i després continua amb el fill.
Una propietat dels BST és que en fer un recorregut en profunditat inorder obtenim els elements ordenats de forma ascendent.
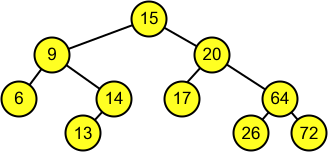
Resultat de fer el recorregut a:
Inorder = [6, 9, 13, 14, 15, 17, 20, 26, 64, 72].
Preorder = [15, 9, 6, 14, 13, 20, 17, 64, 26, 72].
Postorder = [6, 13, 14, 9, 17, 26, 72, 64, 20, 15].
Tipus d'arbres binaris de cerca
[modifica]Hi ha diversos tipus d'arbres binaris de cerca. Els arbre AVL, arbres vermell-negre, són arbres autobalancejables. Els arbres bisellats són arbres també autobalancejables amb la propietat que els elements accedits recentment s'accediran més ràpid en posteriors accessos. Al monticle, com en tots els arbres binaris de cerca, cada node pare té un valor major que els seus fills i a més és complet, és a dir que tots els nivells estan plens amb excepció de l'últim, que pot no estar-ho.
Dues maneres de configurar un arbre binari de cerca podria ser com un arbre complet o degenerat.
Un arbre complet és un arbre amb "n" nivells, on cada nivell d és menor o igual que n-1, el nombre de nodes existents en el nivell "d" és igual que 2d. Això vol dir que tots els possibles nodes existeixen en aquests nivells, no hi ha cap forat. Un requeriment addicional per a un arbre binari complet és que per al nivell "n", els nodes han d'estar ocupats d'esquerra a dreta, i no hi podrà haver un forat a l'esquerra d'un node ocupat.
Un arbre degeneratiu és un arbre que, per a cada node pare, només hi ha associat un node fill; es comporta com una llista enllaçada.
Comparació de rendiment
[modifica]D. A. Heger (2004)[2] realitzà una comparació entre els diferents tipus d'arbres binaris de cerca per trobar quin tipus ens donaria el millor rendiment per a cada cas. Els monticles es troben com el tipus d'arbre binari de cerca que millor resultat mitjana dona, mentre que els arbres vermell-negre els que menor rendiment mitjà ens aporten.
Arbre binari de cerca òptim
[modifica]Si no es pretén planificar un arbre binari de cerca, i sabem exactament amb quina freqüència serà visitat cada element, es pot construir un arbre binari de cerca òptim amb l'objectiu de que la mitjana de despesa generada a l'hora de buscar un element sigui minimitzada. Assumint que coneixem els elements i en quin nivell està cada un, també coneixem la proporció de futures recerques que es faran per trobar aquest element. Si és així, podem utilitzar una solució basada en la programació dinàmica. En canvi, de vegades només tenim l'estimació dels costos de recerca, com passa amb els sistemes que ens mostren el temps que ha necessitat per a realitzar una cerca. Un exemple, si tenim un BST de paraules usat en un corrector ortogràfic, s'hauria d'equilibrar l'arbre basat en la freqüència que té una paraula en el Corpus lingüístic, desplaçant paraules molt freqüents a prop de l'arrel i paraules menys freqúents a prop de les fulles. Un arbre com a tal podria ser comparat amb els arbres Huffman que tracten de trobar elements que són accedits freqüentment a prop de l'arrel per produir una densa informació; de tota manera, els arbres Huffman només poden guardar elements que contenen dades en les fulles i aquests elements no necessiten ser ordenats.
Arbres alfabètics són arbres Huffman amb una restricció d'ordre addicional o cosa que és el mateix, arbres de cerca amb modificació tal que tots els elements són emmagatzemats a les fulles.
Vegeu també
[modifica]Referències
[modifica]- ↑ s. Robert Sedgewick, Kevin Wayne: Algorithms Fourth Edition. Arxivat 2016-10-18 a Wayback Machine. Pearson Education, 2011, ISBN 978-0-321-57351-3, p. 410.
- ↑ Heger, Dominique A. «A Disquisition on The Performance Behavior of Binary Search Tree Data Structures». European Journal for the Informatics Professional, 5, 2004, p. 67-75.
Bibliografia
[modifica]- © Aquest article inclou material de domini públic provinent de l'Institut Nacional d'Estàndards i Tecnologia (NIST). Black, Paul E. Binary Search Tree.
- Mehlhorn, Kurt; Sanders, Peter. Algorithms and Data Structures: The Basic Toolbox. Springer, 2008.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford. «12: Binary search trees, 15.5: Optimal binary search trees». A: Introduction to Algorithms. 2a edició. MIT Press & McGraw-Hill, 2001, p. 253–272, 356–363. ISBN 0-262-03293-7.
- Jarc, Duane J. «Binary Tree Traversals». Interactive Data Structure Visualizations. University of Maryland, 03-12-2005. Arxivat de l'original el 27 de febrer 2014. [Consulta: 13 març 2020].
- Knuth, Donald. «6.2.2: Binary Tree Searching». A: The Art of Computer Programming. 3: "Sorting and Searching". 3rd. Addison-Wesley, 1997, p. 426–458. ISBN 0-201-89685-0.
- Long, Sean. «Binary Search Tree» (PPT). Data Structures and Algorithms Visualization-A PowerPoint Slides Based Approach. SUNY Oneonta.
- Parlante, Nick. «Binary Trees». CS Education Library. Universitat Stanford, 2001.
- «Linus on understanding pointers». [Consulta: 21 febrer 2019].
Enllaços externs
[modifica]- Binary Tree Visualizer (Animació feta amb Javascript de vàries estructures d'arbres binaris)
- Binary Search Tree Exemple en Python Arxivat 2010-03-11 a Wayback Machine.
- «References to Pointers (C++)». MSDN. Microsoft, 2005. (Exemple d'implementació de l'arbre)