Clusterització de dades
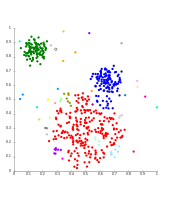
La clusterització de dades és una tècnica molt comuna en l'anàlisi estadística de dades. Bàsicament és la classificació d'objectes similars en diferents grups, o més precisament, la partició de les dades en diferents subconjunts (o clústers). Així doncs, les dades de cada subgrup idealment comparteixen un tret comú.
A grans trets, podem dividir els algorismes en jeràrquics o particionals.
En els primers, es generen clústers successius a partir de clústers ja establerts prèviament. Aquests poden ser aglomeratius si cada element es considera un clúster diferent i posteriorment van agrupant-se. O bé divisoris, si a partir del conjunt sencer es procedeix a dividir-lo en subconjunts més petits. En el segon cas, tots els clústers es determinen en una passada, sovint optimitzant-ho segons un criteri determinat. Al final del procés, es pot tornar a ubicar algunes de les entitats en altres clústers.
Per altra banda, cal destacar les tècniques de cerca per densitat i de 'clumping'. En les primeres, les entitats es consideren com a punts en un espai mètric i normalment es prima la incorporació de nous elements en clústers ja existents abans que crear-ne'n de nous. Les segones es caracteritzen per permetre l'existència de clústers que no siguin disjunts, això és, que els elements puguin incloure's en diferents subgrups simultàniament.
Definició[modifica]
La noció de "clúster" no es pot definir amb precisió, i és per això que hi ha tants algorismes d'agrupació.[1] Hi ha un concepte en comú: un grup d'objectes de dades. Tanmateix, diferents investigadors utilitzen diferents models de clúster, i per a cadascun d'aquests models de clúster es poden donar, de nou, algorismes diferents. La noció de clúster, tal com la troben diferents algorismes, varia significativament en les seves propietats. Entendre aquests "models de clúster" és clau per entendre les diferències entre els diferents algorismes. Els models de clúster típics inclouen:
- Models basats en connectivitat: per exemple, l'agrupació jeràrquica construeix models basats en la connectivitat a distància.
- Model basats en centroides: per exemple, l'algorisme de k-means representa cada clúster mitjançant un únic vector mitjà.
- Models de distribució: els clústers es modelen mitjançant distribucions estadístiques, com ara les distribucions normals multivariables utilitzades per l'algorisme de maximització d'expectativa.
- Models basats en densitat: per exemple, DBSCAN i OPTICS defineixen clústers com a regions denses connectades a l'espai de dades.
- Models basats en subespais: en el biclustering (també conegut com a co-clustering o clustering de dos modes), els clústers es modelen tant amb els membres del clúster com amb els atributs rellevants.
- Models de grup: alguns algorismes no proporcionen un model refinat per als seus resultats i només proporcionen la informació d'agrupació.
- Model basat en grafs: un clique és a dir, un subconjunt de nodes en un graf manera que cada dos nodes del subconjunt estan connectats per una aresta es pot considerar com una forma prototípica de clúster. Les relaxacions del requisit complet de connectivitat (pot faltar una fracció de les vores) es coneixen com a quasi-cliques, com en l'algorisme d'agrupació HCS.
- Models de grafs signats: Cada camí en un gràfic signat té un signe del producte dels signes de les arestes. Sota els supòsits de la teoria de l'equilibri, les arestes poden canviar de signe i donar lloc a un gràfic bifurcat. L'"axioma d'agrupació" més feble (cap cicle té exactament un avantatge negatiu) dóna resultats amb més de dos grups, o subgrafs amb només arestes positives.[2]
- Models neuronals: La xarxa neuronal no supervisada més coneguda és el mapa autoorganitzat i aquests models normalment es poden caracteritzar com a similars a un o més dels models anteriors, i inclouen models basats en subespais quan les xarxes neuronals implementen una forma d'Anàlisi de Components Principals (ACP) o Anàlisi Independent de Components.
Un "agrupament" és essencialment un conjunt d'aquests clústers, que normalment conté tots els objectes del conjunt de dades. A més, pot especificar la relació dels clústers entre si, per exemple, una jerarquia de clústers incrustats entre si. Els agrupaments es poden distingir aproximadament com:
- Clúster dur : cada objecte pertany o no a un clúster
- Agrupació suau (també: agrupació difusa): cada objecte pertany a cada clúster fins a un cert grau (per exemple, una probabilitat de pertànyer al clúster)
També hi ha distincions més concretes, per exemple:
- Clúster de particions estrictes: cada objecte pertany exactament a un clúster.
- Clúster de particions estrictes amb valors atípics : els objectes també poden pertànyer a cap clúster i es consideren dades atípiques.
- Agrupació superposada (també:agrupació alternativa,multivista): els objectes poden pertànyer a més d'un clúster; normalment inclouen cúmuls durs.
- Clúster jeràrquic : els objectes que pertanyen a un clúster fill també pertanyen al clúster pare.
- Agrupació de subespais: Igual que una agrupació superposada, dins d'un subespai definit de manera única, però no s'espera que els clústers se superposin.
Algorismes[modifica]
Tal com s'ha esmentat anteriorment, els algorismes de clúster es poden classificar en funció del seu model de clúster. A continuació només es llisten els exemples més destacats d'algorismes d'agrupació, ja que hi ha més d'un centenar d'algorismes de clúster publicats. No tots proporcionen models per als seus clústers i, per tant, són difícils de categoritzar. (A la llista d'algorismes estadístics es pot trobar una visió general dels algorismes explicats a la Viquipèdia.)
No hi ha cap algorisme d'agrupament "correcte" objectivament, però com es va dir, "l'agrupament està en l'ull de l'espectador".[1] Sovint s'ha de triar empíricament l'algorisme d'agrupació més adequat per cada problema específic, tret que hi hagi una raó matemàtica per la qual un model de clúster sigui millor respecte a la resta.[1] Un algorisme dissenyat per a un tipus de model generalment fallarà en un conjunt de dades que conté un tipus de model radicalment diferent. Per exemple, el k-means no pot trobar clústers no convexos.[1]
Clúster basat en connectivitat (agrupació jeràrquica)[modifica]
L'agrupació basada en la connectivitat, també coneguda com a agrupació jeràrquica, es basa en la idea que els objectes estan més relacionats amb objectes propers que amb objectes més allunyats. Aquests algorismes connecten "objectes" per formar "clústers" en funció de la seva distància. Un clúster es pot descriure en gran manera per la distància màxima necessària per a connectar parts del clúster. A diferents distàncies es formaran diferents clústers, que es poden representar mitjançant un dendrograma. D’aquí és d'on ve el nom "agrupació jeràrquica". Aquests algorismes no proporcionen una única partició del conjunt de dades, sinó que proporcionen una àmplia jerarquia de clústers que es fusionen entre ells en determinades distàncies. En un dendrograma, l'eix Y marca la distància a la qual es fusionen els clústers, mentre que els objectes es col·loquen al llarg de l'eix X de manera que els grups no es barregin.
El clustering basat en la connectivitat comprèn un conjunt de mètodes que es diferencien per la manera com es calculen les distàncies. A part de l'elecció habitual de funcions de distància, l'usuari també ha de decidir el criteri d'enllaç a utilitzar (atès que un clúster consta de diversos objectes, hi ha diversos candidats per a calcular la distància). Les opcions més comuns com a criteri d'enllaç es coneixen com a agrupació d'enllaç únic (el mínim de distàncies d'objecte), agrupació d'enllaç complet (el màxim de distàncies d'objecte) i UPGMA o WPGMA("Mètode de grups de parells no ponderats o ponderats amb mitjana aritmètica", també conegut com a agrupació d'enllaços mitjans). A més, l'agrupació jeràrquica pot ser aglomerativa (començant amb elements únics i agregant-los en clústers) o divisòria (començant pel conjunt de dades complet i dividint-lo en particions).
Aquests mètodes no produiran una partició única del conjunt de dades, sinó una jerarquia a partir de la qual l'usuari encara haurà de triar els clústers adequats. No són molt robusts cap a les dades atípiques, que es mostraran com a clústers addicionals o fins i tot provocaran que altres clústers es fusionin (el que es coneix com a "fenomen d'encadenament", en particular amb l'agrupament d'enllaç únic). En el cas general, la complexitat és per al clustering aglomeratiu i per a l'agrupament divisiu,[3] que els fa massa lents per a grans conjunts de dades. Per a alguns casos especials, es coneixen mètodes òptims eficients (de complexitat ): SLINK[4] per a l'enllaç únic i CLINK[5] per a l'agrupació d'enllaços complets.
- Exemples de agrupació d'enllaços
-
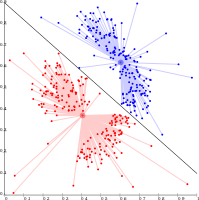
Enllaç únic sobre dades gaussianes. Amb 35 clústers, el clúster més gran comença a fragmentar-se en parts més petites, mentre que abans encara estava connectat al segon més gran a causa de l'efecte d'enllaç únic.
-
Enllaç únic en clústers basats en la densitat. S'han extret 20 clústers, la majoria dels quals contenen elements únics, ja que l'agrupació d'enllaços no té una noció de "soroll".
Clúster basat en centroides[modifica]
Article principal: k-means clustering
En l'agrupació basada en centroides, cada clúster està representat per un vector central, que no és necessàriament un membre del conjunt de dades. Quan el nombre de clústers es fixa en k, k-means dóna una definició formal com a problema d'optimització: troba els k centres del clúster i assigna els objectes al centre del clúster més proper, de manera que les distàncies del clúster es minimitzin.
Se sap que el problema d'optimització en si és NP-complex i, per tant, l'enfocament comú és buscar només solucions aproximades. Un mètode aproximat particularment conegut és l'algorisme de Lloyd, sovint anomenat " algorisme k-means ". Tanmateix, només troba un òptim local i s'executa diverses vegades amb diferents inicialitzacions aleatòries. Les variacions de k -means sovint inclouen optimitzacions com l'elecció del millor de múltiples execucions, però també restringir els centroides als membres del conjunt de dades (k-medoids), escollint les mitjanes(k-medians clustering), escollint els centres inicials de manera menys aleatòria (k-means++) o permetent una assignació de clúster difusa (fuzzy c-means).
La majoria dels algorismes de tipus k - means requereixen que el nombre de clústers –k– s'especifiqui, cosa que es considera un dels majors inconvenients d'aquests algorismes. A més, els algorismes prefereixen clústers de mida similar, ja que sempre assignaran un objecte al centroide més proper. Això sovint condueix a tallar incorrectament les vores dels clústers (fet que no és sorprenent, ja que l'algoritme optimitza els centres del clúster, no les vores del clúster).
Els K-means tenen una sèrie de propietats teòriques interessants. En primer lloc, divideix l'espai de dades en una estructura coneguda com a diagrama de Voronoi. En segon lloc, conceptualment s'acosta a la classificació del veí més proper i, per tant, és popular en l'aprenentatge automàtic. En tercer lloc, es pot veure com una variació de l'agrupament basat en models i l'algoritme de Lloyd com una variació de l'algoritme de maximització d'expectatives per a aquest model que es discuteix a continuació.
- Exemples de k-means
-
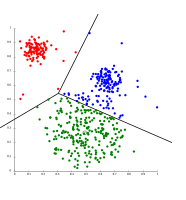
k-means separa les dades en cel·les de Voronoi, les quals asumeixen clústers de la mateixa mida.
-
k-means no pot representar clusters basats en la densitat
Els problemes d'agrupament basats en centroides, com ara k-means i k-medoids, són casos especials del problema d'ubicació d'instal·lacions, un problema canònic a les comunitats de recerca d'operacions i geometria computacional. En un problema bàsic d'ubicació d'instal·lacions (del qual hi ha nombroses variants que modelen configuracions més elaborades), la tasca és trobar les millors ubicacions de magatzem per atendre de manera òptima un conjunt determinat de consumidors. Es poden veure els "magatzems" com a centroides de clúster i les "ubicacions dels consumidors" com les dades que s'han d'agrupar. Això fa possible aplicar les solucions algorítmiques ben desenvolupades pel problema de les instal·lacions al problema d'agrupació basat en el centroide que s’està considerant.
Agrupació basada en la distribució[modifica]
El model de clustering més relacionat amb l'estadística es basa en models de distribució. Aleshores, els components dels clústers es poden definir fàcilment com a objectes que pertanyen molt probablement a la mateixa distribució. Una propietat a mencionar d'aquest enfocament és que s'assembla molt a la manera en què es generen conjunts de dades artificials: mitjançant el mostreig d'objectes aleatoris d'una distribució.
Tot i que la base teòrica d'aquests mètodes és excel·lent, pateixen un problema clau conegut com a overfitting. Es pot evitar imposant restriccions a la complexitat del model. Un model més complex normalment serà capaç d'explicar millor les dades, cosa que dificulta inherentment l'elecció de la complexitat del model adequat.
Un mètode destacat és el conegut com a models de mescles gaussianes (utilitzant l'algorisme de maximització d'expectativa). Aquí, el conjunt de dades normalment es modela amb un nombre fix (per evitar l'ajustament excessiu) de distribucions gaussianes. Aquestes s'inicien aleatòriament i els seus paràmetres s'optimitzen iterativament per adaptar-se millor al conjunt de dades. Això convergirà a un òptim local, de manera que diverses execucions poden produir resultats diferents. Per tal d'obtenir un agrupament robust, els objectes sovint s'assignen a la distribució gaussiana a la qual probablement pertanyen; per a agrupacions suaus, això no és necessari.
L'agrupació basada en la distribució produeix models complexos per a clústers que poden capturar la correlació i la dependència entre els atributs. No obstant això, aquests algorismes suposen una càrrega addicional per a l'usuari: per a molts conjunts de dades reals, pot ser que no hi hagi un model matemàtic definit de manera concisa (per exemple, assumir distribucions gaussianes és una hipòtesi força forta sobre les dades).
- Exemples d'agrupament de models de mescles gaussianes
-
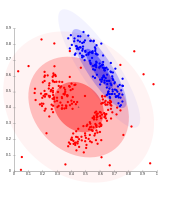
En dades distribuïdes per Gauss, l'algorisme de maximització d'expectativa funciona bé, ja que utilitza gaussianes per modelar clústers
-
Els clústers basats en la densitat no es poden modelar mitjançant distribucions gaussianes
Agrupament basat en la densitat[modifica]
En l'agrupació basada en la densitat,[6] els clústers es defineixen com a àrees de densitat més alta que la resta del conjunt de dades. Els objectes en zones disperses, que són necessaris per separar grups, solen considerar-se com a punts de soroll i de frontera.
El mètode de agrupació basat en la densitat més popular[7] és DBSCAN. En contrast amb molts mètodes més nous, inclou un model de clúster ben definit anomenat "densitat-accessibilitat". Similar a l'agrupament basat en enllaços, es basa en connectar punts a partir de determinats llindars de distància. Tanmateix, només connecta punts que compleixen un criteri de densitat, en la variant original definit com un nombre mínim d'altres objectes dins d'aquest radi. Un clúster consta de tots els objectes connectats per densitat (que poden formar un clúster de forma arbitrària, en contrast amb molts altres mètodes), a més de tots els objectes que es troben dins de l'abast d'aquests objectes. Una altra propietat interessant de DBSCAN és que la seva complexitat és bastant baixa (requereix un nombre lineal de consultes d'interval a la base de dades) i que descobreix essencialment els mateixos resultats a cada tirada, (per als punts centrals i de soroll sí, però no per als punts de frontera), sent així un algorisme determinista, i que per tant, no cal executar-lo diverses vegades. L'algorisme OPTICS és una generalització de DBSCAN que elimina la necessitat de triar un valor adequat per al paràmetre d'interval [e], i produeix un resultat jeràrquic relacionat amb el de l'agrupació d'enllaços. DeLi-Clu, Density-Link-Clustering combina idees de l'agrupament d'enllaç únic i OPTICS, eliminant el paràmetre completament i oferint millores de rendiment mitjançant l'ús d'un índex d'arbre-R.
El principal inconvenient de DBSCAN i OPTICS és que esperen algun tipus de caiguda de densitat per detectar les fronteres del clúster. En conjunts de dades amb, per exemple, distribucions gaussianes superposades, un cas d'ús comú en dades artificials, les vores del clúster produïdes per aquests algorismes sovint semblen arbitràries, perquè la densitat del clúster disminueix contínuament. En un conjunt de dades format per mescles de gaussianes, aquests algorismes gairebé sempre es veuen superats per mètodes com l'agrupació per maximització d'expectativa, que sí són capaços de modelar amb precisió aquest tipus de dades.
El mean-shift és un enfocament d'agrupació en què cada objecte es mou a l'àrea més densa de la seva proximitat, basat en l'estimació de la densitat del nucli. Finalment, els objectes convergeixen als màxims locals de densitat. De manera semblant a l'agrupació de k-means, aquests "atractors de densitat" poden servir com a representants del conjunt de dades, però el mean-shift pot detectar clústers de forma arbitraria similars a DBSCAN. A causa del costós procediment iteratiu i de l'estimació de la densitat, el mean-shift sol ser més lent que DBSCAN o k-means. A més d'això, l'aplicabilitat de l'algoritme de mean-shift a dades multidimensionals es veu obstaculitzada pel comportament poc suau de l'estimació de la densitat del nucli, que provoca una sobrefragmentació de les cues de clúster.
- Exemples d'agrupaments basats en la densitat
-
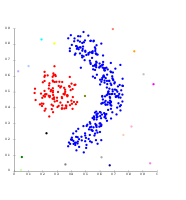
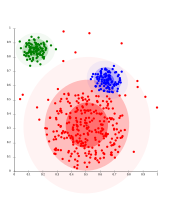
Agrupació basada en la densitat amb DBSCAN.
-
DBSCAN assumeix clústers de densitat similar i pot tenir problemes per separar clústers propers
-
OPTICS és una variant DBSCAN, que millora el maneig de clústers de diferents densitats
Agrupació basada en quadrícula[modifica]
La tècnica basada en quadrícula s'utilitza per a un conjunt de dades multidimensional.[8] En aquesta tècnica, creem una estructura de quadrícula, i la comparació es realitza entre les cel·les. Aquest sistema basat en quadrícules és ràpid i té una complexitat computacional baixa. Hi ha dos tipus de mètodes d'agrupació basats en graelles: STING i CLIQUE.
Els passos implicats en l'algorisme d'agrupació basat en graelles són:
- Dividir l'espai de dades en un nombre finit de cel·les.
- Seleccionar aleatòriament una cel·la 'c', on 'c' no s'hauria d'haver recorregut abans.
- Calcular la densitat de 'c'
- Si la densitat de 'c' és superior a la densitat del llindar
- Marcar la cel·la "c" com a clúster nou
- Calcular la densitat de tots els veïns de 'c'
- Si la densitat d'una cel·la veïna és superior a la densitat del llindar, afegir la cel·la al clúster i repetir els passos 4.2 i 4.3 fins que no hi hagi cap veí amb una densitat superior a la densitat del llindar.
- Repetir els passos 2, 3 i 4 fins que es recorrin totes les cel·les.
- Aturar.
Avaluació i valoració[modifica]
L'avaluació o validació dels resultats del clustering és tan difícil com la pròpia agrupació.[9] Els plantejaments més comuns inclouen l'avaluació " interna ", on l'agrupació es resumeix en un únic valor de qualitat, l'avaluació " externa ", on l'agrupació es compara amb una classificació ja existent de "veritat bàsica", l'avaluació " manual " duta a terme per un expert, i l'avaluació "indirecta" mitjançant l'avaluació de la utilitat del clustering en la seva aplicació.[10]
Les mesures d'avaluació interna pateixen un problema, representen funcions que per elles mateixes poden ser l'objectiu d'un clustering. Per exemple, es pot agrupar el conjunt de dades pel coeficient Silhouette; tot i que no es coneix cap algorisme eficient per fer-ho. Mitjançant l'ús de mesures d'avaluació interna com aquesta, un compara abans la similitud dels problemes d'optimització,[10] i no necessàriament com d'útil és el propi clustering.
L'avaluació externa té problemes similars: si tenim aquestes etiquetes de "veritat bàsica", llavors no ens fa falta fer clustering; i en aplicacions pràctiques normalment no tenim aquestes etiquetes. D'altra banda, les etiquetes només mostren una possible partició del conjunt de dades, la qual cosa no implica que no existeixi una agrupació diferent, i potser millor.
Per tant, cap d'aquests enfocaments pot jutjar en última instància la qualitat real d'una agrupació, per això es necessita l'avaluació humana,[10] que és molt subjectiva. No obstant, aquestes estadístiques poden ser força informatives per identificar agrupacions dolentes.[11]
Avaluació interna[modifica]
Vegeu també: Determinació del nombre de clústers en un conjunt de dades
Quan un resultat d'agrupació s'avalua en funció de les dades que es van agrupar, això s'anomena avaluació interna. Aquests mètodes solen assignar la millor puntuació a l'algorisme que produeix clústers amb una gran similitud dins d'un clúster i una baixa similitud entre clústers. Un inconvenient d'utilitzar criteris interns en l'avaluació de clústers és que les puntuacions altes en una mesura interna no donen necessàriament com a resultat aplicacions efectives de recuperació d'informació. A més, aquesta avaluació està esbiaixada cap a algorismes que utilitzen el mateix model de clúster. Per exemple, l'agrupació k-means optimitza de manera natural les distàncies dels objectes, i un criteri intern basat en la distància probablement sobrevalorarà l'agrupació resultant.
Per tant, les mesures d'avaluació interna són les més adequades per obtenir una visió de situacions en què un algorisme funciona millor que un altre, però això no implica que un algorisme produeixi resultats més vàlids que un altre. La validesa mesurada per aquest índex depèn que aquest tipus d'estructura existeixi en el data set. Un algorisme dissenyat per a algun tipus de models no serà viable si el data set conté un conjunt de models radicalment diferent, o si l'avaluació mesura un criteri radicalment diferent. Per exemple, k-means només pot trobar clústers convexos, i molts índexs d'avaluació assumeixen clústers convexos. En un conjunt de dades amb clústers no convexos ni l'ús de k-means, ni d'un criteri d'avaluació que assumeixi convexitat, seria correcte.
Existeixen més d'una dotzena de mesures d'avaluació interna, generalment basades en la intuïció que els ítems d'un mateix clúster haurien de ser més semblants que els ítems de diferents clústers. : 115–121 Per exemple, es poden utilitzar els mètodes següents per avaluar la qualitat dels algorismes d'agrupació basats en criteris interns:
- Índex de Davies-Bouldin: L' índex de Davies-Bouldin es pot calcular mitjançant la fórmula següent: on n és el nombre de clústers, és el centroide del clúster , és la distància mitjana de tots els elements del clúster al centroide , i és la distància entre els centroides i . Com que els algorismes que produeixen clústers amb distàncies baixes intra-clúster (alta similitud intra-clúster) i altes distàncies entre clústers (baixa similitud entre clúster) tindran un baix índex de Davies–Bouldin, l'algoritme d'agrupació que produeix una col·lecció de clústers amb l'índex de Davies-Bouldin més petit es considera el millor algorisme segons aquest criteri.
- Índex de Dunn: L'índex de Dunn pretén identificar grups densos i ben separats. Es defineix com la proporció entre la distància mínima entre-clúster i la distància màxima intra-clúster. Per a cada partició de clúster, l'índex de Dunn es pot calcular mitjançant la fórmula següe on d (i, j) representa la distància entre els cúmuls i i j, i d '(k) mesura la distància intra-cluster del cúmul k. La distància entre clústers d (i, j) entre dos clústers pot ser qualsevol nombre de mesures de distància, com ara la distància entre els centroides dels clústers. De la mateixa manera, la distància intra-clúster d '(k) es pot mesurar de diverses maneres, com ara la distància màxima entre qualsevol parell d'elements del clúster k.. Atès que els criteris interns busquen clústers amb una alta similitud intra-clúster i una baixa similitud entre clústers, són millors els algorismes que produeixen clústers amb un alt índex de Dunn.
- Coeficient de “Silhouette”: El coeficient de “Silhouette” contrasta la distància mitjana als elements del mateix clúster amb la distància mitjana als elements d'altres clústers. Els objectes amb un valor de “Silhouette” alt es consideren ben agrupats, els objectes amb un valor baix poden ser valors atípics (outliers). Aquest índex funciona bé amb k -means, [ citació necessària ] i també s'utilitza per determinar el nombre òptim de clusters.
Avaluació externa[modifica]
En l'avaluació externa, els resultats del clustering s'avaluen a partir de dades que no s'han utilitzat per a l'agrupació, com ara les etiquetes de classe conegudes i els punts de referència externs. Aquests punts de referència consisteixen en un conjunt d'elements prèviament classificats, i aquests conjunts solen ser creats per humans (experts). Així, els conjunts de referència es poden considerar com un estàndard d'or per a l'avaluació.[12] Aquests tipus de mètodes d'avaluació mesuren la proximitat de l'agrupació resultant a les classes de referència predeterminades. Tanmateix, recentment s'ha discutit si això és adequat per a dades reals, o només en conjunts de dades sintètiques amb una veritat bàsica de fets, com que les classes poden contenir estructura interna, els atributs presents poden no permetre la separació de clústers o les classes poden contenir anomalies. A més, des del punt de vista del descobriment del coneixement, la reproducció del coneixement conegut pot no ser necessàriament el resultat previst. En l'escenari especial de l'agrupació restringida, on la metainformació (com les etiquetes de classe) ja s'utilitza en el procés d'agrupació, la retenció d'informació per a finalitats d'avaluació no és trivial.
Una sèrie de mesures s'adapten a partir de variants utilitzades per avaluar les tasques de classificació. En lloc de comptar el nombre de vegades que una classe s'ha assignat correctament a un únic punt de dades (conegut com a veritables positius), aquestes mètriques de recompte de parells avaluen si es preveu que cada parell de punts de dades que es troba realment al mateix clúster estiguin al mateix clúster.
Igual que amb l'avaluació interna, existeixen diverses mesures d'avaluació externa, :[13] per exemple:
- Puresa: la puresa és una mesura que consisteix en mirar fins a quin punt els clusters contenen una única classe.[14] El seu càlcul es pot pensar de la següent manera: Per a cada clúster, compta el nombre de dades de la classe més comuna dins del mateix. A continuació es fa la suma de tots els clústers i es divideix pel nombre total de punts de dades. Formalment, donat algun conjunt de clústers i algun conjunt de classes , ambdues punts de dades, la puresa es pot definir com:
- Aquesta mesura no penalitza que es tingui molts clústers, i tenir més clústers facilitarà l'obtenció d'una gran puresa. Sempre és pot aconseguir una puntuació de puresa d'1 posant cada punt de dades al seu propi clúster. A més, la puresa no funciona bé per a les dades desequilibrades, on fins i tot els algorismes d'agrupament amb un rendiment deficient donaran un valor de puresa elevat. Per exemple, si un conjunt de dades de mida 1000 consta de dues classes, una que conté 999 punts i l'altra que conté 1 punt, llavors cada partició possible tindrà una puresa d'almenys el 99,9%.
- Índex Rand
- L'índex Rand calcula com de semblants són els clústers (retornats per l'algoritme de clúster) amb les classificacions de referència. Es pot calcular mitjançant la fórmula següent:
- on és el nombre de veritables positius, és el nombre de veritables negatius, és el nombre de falsos positius, i és el nombre de falsos negatius. Les instàncies que es compten aquí són el nombre d'assignacions de parelles correctes. és el nombre de parells de punts que que coincideixen tant en la partició prevista com en a la partició real, en canvi és el nombre de parells de punts que apareixen en la partició prevista però no en la partició real.
- Si tenim un conjunt de dades de mida N, llavors .
- Mesura F
- La Mesura F es pot utilitzar per equilibrar la contribució de falsos negatius ponderant el recall mitjançant un paràmetre . Tenint en compte que la precisió i el recall estan definits de la següent manera (ambdós són mesures d'avaluació per ells mateixos) :
- on és la precisió i el recalls De manera que la Mesura F és calcula mitjançant la fórmula que apareix a continuaciófollowing formula:[15]
- On , . Dit d'una altra manera, el recall no afecta en la Mesura F quan , a més si incrementem el valor de incrementa també el pes que té el recall.
- L'índex de Jaccard s'utilitza per quantificar la similitud entre dos conjunts de dades. L'índex de Jaccard pren un valor entre 0 i 1. Un índex d'1 significa que els dos conjunts de dades són idèntics i un índex de 0 indica que els conjunts de dades no tenen elements comuns. L'índex de Jaccard es defineix per la fórmula següent:
- Aquest és simplement el nombre d'elements únics comuns a tots dos conjunts dividit pel nombre total d'elements únics dels dos conjunts.
- Els també no es tenen en compte i pot variar des de 0 cap amunt sense límit.
- Índex de daus
- La mesura simètrica de Daus duplica el pes de i seguiex ignorant els :
- Índex de Fowlkes–Mallows[16]
- L'índex de Fowlkes-Mallows calcula la similitud entre els clústers retornats per l'algorisme de clúster i les classificacions de referència. Com més alt sigui el valor de l'índex Fowlkes-Mallows, més semblants són els clústers i les classificacions de referència. Es pot calcular mitjançant la fórmula següent:
- on és el nombre de veritables positius, és el nombre de falsos positius i és el nombre de falsos negatius. El índex és la mitjana geomètrica de la precisió i el reclam i , i per tant també es coneix com a mesura G, mentre que la mesura F és la seva mitjana harmònica.[17][18] A més, la precisió i el reclam també es coneixen com índexs de Wallace i .
- La informació mútua és una mesura teòrica de la informació que ens indica quanta informació es comparteix entre un clustering i una classificació, de la qual es coneix els valors reals, que pot detectar una similitud no lineal entre dues agrupacions. La informació mútua normalitzada és una família de variants corregides per atzar que té un biaix reduït per als números de clúster variables.[9]
- Matriu de confusió: Es pot utilitzar una matriu de confusió per visualitzar ràpidament els resultats d'un algorisme de classificació (o agrupació). Mostra com de diferent és un clúster del clúster estàndard d'or.
Tendència d'agrupament[modifica]
Mesurar la tendència del clúster és mesurar fins a quin punt existeixen clústers a les dades que s'han d'agrupar, i es pot realitzar com a prova inicial, abans d'intentar l'agrupació. Una manera de fer-ho és comparar les dades amb dades aleatòries. De mitjana, les dades aleatòries no haurien de tenir clústers:
- Hi ha múltiples formulacions de l'estadística de Hopkins.[19] Un típic és el següent.[20] Sigui el conjunt de punts de dades en un espai -dimensional. Considereu una mostra aleatòria (sense substitució) de punts de dades amb els membres. També genereu un conjunt de punts de dades uniformement distribuïts aleatòriament. Ara defineix dues mesures de distància, on sigui la distància de des del seu veí més proper en X i sigui la distància de del seu veí més proper a X. Aleshores definim l'estadística de Hopkins com:
- Amb aquesta definició, les dades aleatòries uniformes haurien de tendir a tenir valors propers a 0,5 i les dades agrupades haurien de tenir valors més propers a 1.
- Tanmateix, les dades que contenen només una gaussiana també tindran una puntuació propera a 1, ja que aquesta estadística mesura la desviació d'una distribució uniforme, no multimodalitat, fent que aquesta estadística sigui en gran manera inútil en l'aplicació (ja que les dades reals mai són uniformes de manera remota).
Referències[modifica]
- ↑ 1,0 1,1 1,2 1,3 Estivill-Castro, Vladimir «Why so many clustering algorithms – A Position Paper». ACM SIGKDD Explorations Newsletter. ACM SIGKDD Explorations Newsletter, 4, 1, 20-06-2002, pàg. 65-75. DOI: 10.1145/568574.568575.
- ↑ James A. Davis (May 1967) "Clustering and structural balance in graphs", Human Relations 20:181–7
- ↑ Everitt, Brian. Cluster analysis. Chichester, West Sussex, U.K: Wiley, 2011. ISBN 9780470749913.
- ↑ Sibson, R. SLINK: an optimally efficient algorithm for the single-link cluster method. The Computer Journal, 16, 1, 1973, pàg. 30–34. DOI: 10.1093/comjnl/16.1.30.
- ↑ Defays, D. An efficient algorithm for a complete link method. The Computer Journal, 20, 4, 1977, pàg. 364–366. DOI: 10.1093/comjnl/20.4.364.
- ↑ Kriegel, Hans-Peter; Kröger, Peer; Sander, Jörg; Zimek, Arthur «Còpia arxivada». Density-based Clustering. WIREs Data Mining and Knowledge Discovery, 1, 3, 2011, pàg. 231-240. Arxivat de l'original el 2016-11-17. DOI: 10.1002/widm.30 [Consulta: 27 juny 2022].
- ↑ Microsoft academic search: most cited data mining articles Arxivat 2010-04-21 a Wayback Machine.: DBSCAN està al rank 24, havent-hi accedit el: 27/06/2022
- ↑ Data Clustering : Algorithms and Applications. ISBN 978-1-315-37351-5.
- ↑ 9,0 9,1 Pfitzner, Darius; Leibbrandt, Richard; Powers, David Characterization and evaluation of similarity measures for pairs of clusterings. Knowledge and Information Systems, 19, 3, 2009, pàg. 361–394. DOI: 10.1007/s10115-008-0150-6.
- ↑ 10,0 10,1 10,2 Feldman, Ronen; Sanger, James. The Text Mining Handbook: Advanced Approaches in Analyzing Unstructured Data. Cambridge Univ. Press, 2007. ISBN 978-0521836579. OCLC 915286380.
- ↑ Weiss, Sholom M.; Indurkhya, Nitin; Zhang, Tong; Damerau, Fred J. Text Mining: Predictive Methods for Analyzing Unstructured Information. Springer. ISBN 978-0387954332. OCLC 803401334.
- ↑ Pfitzner, Darius; Leibbrandt, Richard; Powers, David «Characterization and evaluation of similarity measures for pairs of clusterings». Knowledge and Information Systems, 19, 3. DOI: 10.1007/s10115-008-0150-6 [Consulta: 2009].
- ↑ Knowledge Discovery in Databases – Part III – Clustering, 2017.
- ↑ Manning, Christopher D.; Raghavan, Prabhakar; Schütze, Hinrich. Introduction to Information Retrieval. Cambridge University Press, 2008-07-07. ISBN 978-0-521-86571-5.
- ↑ Manning, Christopher D.; Raghavan, Prabhakar; Schütze, Hinrich. Introduction to Information Retrieval. Cambridge University Press, 2008-07-07. ISBN 978-0-521-86571-5.
- ↑ Fowlkes, E. B.; Mallows, C. L. A Method for Comparing Two Hierarchical Clusterings. Journal of the American Statistical Association, 78, 383, 1983, pàg. 553–569. DOI: 10.1080/01621459.1983.10478008. JSTOR: 2288117.
- ↑ Powers, David (2003). "Recall and Precision versus the Bookmaker" a International Conference on Cognitive Science. : 529–534
- ↑ Arabie, P. Comparing partitions. Journal of Classification, 2, 1, 1985. DOI: 10.1007/BF01908075.
- ↑ Hopkins, Brian; Skellam, John Gordon A new method for determining the type of distribution of plant individuals. Annals of Botany, 18, pàg. 213–227. DOI: 10.1093/oxfordjournals.aob.a083391.
- ↑ Banerjee, A. Validating clusters using the Hopkins statistic. IEEE International Conference on Fuzzy Systems, 1, 2004, pàg. 149–153. DOI: 10.1109/FUZZY.2004.1375706.
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Clusterització de dades |
Everitt, B. (1974) Cluster Analysis. (1a ed). Heinemann Educational Books Ltd. ISBN 0-435-82297-7