Graf complet

En el camp matemàtic de la teoria de grafs, un graf complet és un graf simple on una aresta conecta tots els parells de vèrtex. El graf complet amb $n$ vèrtex té $n$ v+ertex i $n(n-1)/2$ arestes, i es donat amb $K_n$. És un graf regular de grau $n-1$. Tots els grafs complets són els seus propis cicles. Estan màximament conectats de forma que l'únic tall de vèrtex que desconecta el graf és tot el conjunt de vèrtex.

Un graf complet amb n-nodes representa les arestes d'un n-simplex. Geomètricament $K_3$ està relacionat amb un triangle, $K_4$ amb un tetràedre, $K_5$ un pentacoron, etc.

El teorema de Kuratowski diu que un graf planar no pot contenir $K_5$ (o el graf bipartit complet $K_{3,3}$) com un menor). Com que $K_n$ inclou $K_{n-1}$, no hi ha grafs $K_n$ amb $n>=5$ que siguin planars.

Una propietat important dels grafs complets és el nombre quadràtic de connexions. Això vol dir que el nombre d'arestes és una funció quadràtica del nombre de nodes. Per tant, un graf complet pot ser el pitjor cas per grans sistemes conectats com xarxes socials i xarxes d'ordinadors.

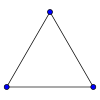
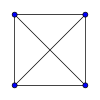
Els grafs complets amb $n$ vèrtex, per a $n$ entre 1 i 8, es mostren a continuació amb el nombre de connexions:

$K_1: 0$	$K_2: 1$	$K_3: 3$	$K_4: 6$
$K_5: 10$	$K_6: 15$	$K_7: 21$	$K_8: 28$

Enllaços externs

• Counting Paths and Cycles in Complete Graphs. Results are available Mehdi Hassani, Cycles in graphs and derangements, Math. Gaz. 88(March 2004) pp. 123-126 (reprint) or here