Llista de grups petits

Aquest article mostra una llista matemàtica dels grups finits d'ordre baix (una cardinalitat de fins a 16 elements) classificats per isomorfisme de grups.

Amb aquesta llista es pot determinar a quin grup conegut és isomorf un grup finit G donat: Cerqueu primer l'ordre de G, seguidament cerqueu els candidats per aquell ordre a la llista. Si sabeu si G és o no és abelià potser podreu descartar alguns candidats. Per a distingir entre els candidats restants podeu mirar l'ordre dels elements de G i comparar-los amb els ordres dels elements dels candidats.

Terminologia[modifica]

El signe d'igualtat "=" denota isomorfisme de grups.

C_n: el grup cíclic d'ordre n (es correspon amb el grup additiu de ℤ/nℤ, denotat de vegades ℤ_n).
D_n: el grup dièdric d'ordre 2n (de vegades s'usa la notació D_2n o D_2,n)
S_n: el grup simètric que conté les n! permutacions d'un conjunt de n elements.
A_n: el grup alternat amb les n!/2 permutacions de S_n que tenen signe parell.
Dic_n: el grup dicíclic d'ordre 4n.

La notació G × H indica el producte directe de dos grups; Gⁿ indica el producte directe d'un grup amb ell mateix n vegades. $G\rtimes H$ vol dir el producte semidirecte on H actua sobre G; si l'acció particular de H sobre G s'omet és que totes les accions no trivials possibles donen el mateix grup producte llevat d'isomorfisme.

S'indiquen els que són grups abelians i els que són grups simples. (Per als grups d'ordre n < 60, els grups simples són exactament els grups cíclics C_n, per a n primer).

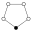
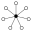
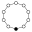
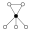
L'element neutre està representat per un cercle negre als grafs dels cicles. L'ordre més petit per al qual el graf no representa unívocament un grup és ordre 16.

A les llistes de subgrups, el grup trivial i el mateix grup no apareixen indicats. Als casos on hi ha múltiples subgrups isomorfs, el nombre d'aparicions s'indica entre parèntesis.

Llista de grups abelians petits[modifica]

Els grups abelians finits es classifiquen fàcilment: són grups cíclics o els seus productes directes. El teorema xinès del residu ens pot ajudar a trobar els isomorfismes amb aquests productes directes. Els grups abelians finitament generats també es poden classificar. Vegeu més informació a l'article grup abelià.

Ordre	Grup	Subgrups	Propietats	Graf dels cicles
1	grup trivial = C₁ = S₁ = A₂	-	trivialment té propietats diverses	Graf dels cicles per al grup trivial
2	C₂ = S₂ = D₁	-	simple, el grup no trivial més petit	Graf dels cicles per al grup C2
3	C₃ = A₃	-	simple	Graf dels cicles per al grup C3
4	C₄	C₂		Graf dels cicles per al grup C4
4	Grup de Klein = C₂ × C₂ = D₂	C₂ (3)	el grup no cíclic més petit	Graf dels cicles per al grup de Klein D2
5	C₅	-	simple	Graf dels cicles per al grup C5
6	C₆ = C₃ × C₂	C₃, C₂		Graf dels cicles per al grup C6
7	C₇	-	simple	Graf dels cicles per al grup C7
8	C₈	C₄, C₂		Graf dels cicles per al grup C8
	C₄ × C₂	C₂², C₄ (2), C₂ (3)		Graf dels cicles per al grup C4 × C2
	C₂³	C₂² (7), C₂ (7)		Graf dels cicles per al grup C2^3
9	C₉	C₃		C9
9	C₃²	C₃ (4)		Graf dels cicles per al grup C3^2
10	C₁₀ = C₅ × C₂	C₅, C₂		C10
11	C₁₁	-	simple	C11
12	C₁₂ = C₄ × C₃	C₆, C₄, C₃, C₂		C12
12	C₆ × C₂ = C₃ × C₂²	C₆ (3), C₃, C₂ (3), C₂²		Graf dels cicles per al grup C3 × C2^2
13	C₁₃	-	simple	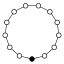C13
14	C₁₄ = C₇ × C₂	C₇, C₂		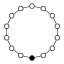C14
15	C₁₅ = C₅ × C₃	C₅, C₃		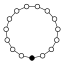C15
16	C₁₆	C₈, C₄, C₂		C16
	C₂⁴	C₂ (15), C₂² (35), C₂³ (15)		Graf dels cicles per al grup C2^4
	C₄ × C₂²	C₂ (7), C₄ (4), C₂² (7), C₂³, C₄ × C₂ (6)		Graf dels cicles per al grup C4 × C2^2
	C₈ × C₂	C₂ (3), C₄ (2), C₂², C₈ (2), C₄ × C₂		Graf dels cicles per al grup C8 × C2
	C₄²	C₂ (3), C₄ (6), C₂², C₄ × C₂ (3)		Graf dels cicles per al grup C4^2

Llista de grups no abelians petits[modifica]

Ordre	Grup	Subgrups	Propietats	Graf dels cicles
6	S₃ = D₃	C₃, C₂ (3)	el grup no abelià més petit	S3
8	D₄	C₄, C₂² (2), C₂ (5)		D4
8	Grup dels quaternions, Q₈ = Dic₂	C₄ (3), C₂	el grup hamiltonià més petit	Grup dels quaternions Q8
10	D₅	C₅, C₂ (5)		D5
12	D₆ = D₃ × C₂	C₆, D₃ (2), C₂² (3), C₃, C₂ (7)		D6
	A₄	C₂², C₃ (4), C₂ (3)	el grup més petit que demostra que un grup no ha de tenir forçosament un subgrup de cada ordre que divideix l'ordre del grup: no té cap subgrup d'ordre 6 (en contra del recíproc al teorema de Lagrange, com ja indiquen els teoremes de Sylow.)	A4
	Dic₃ = $C_{3}\rtimes C_{4}$	C₂, C₃, C₄ (3), C₆		Dic3
14	D₇	C₇, C₂ (7)		D7
16^[1]	D₈	C₈, D₄ (2), C₂² (4), C₄, C₂ (9)		D8
	D₄ × C₂	D₄ (2), C₄ × C₂, C₂³ (2), C₂² (11), C₄ (2), C₂ (11)		D4 × C2
	Grup generalitzat dels quaternions Q₁₆ = Dic₄			Grup generalitzat dels quaternions Dic4
	Q₈ × C₂		grup hamiltonià	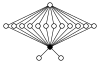Q8 × C2
	El grup quasidièdric d'ordre 16			Grup quasidièdric d'ordre 16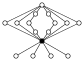
	El grup d'Iwasawa d'ordre 16			grup d'Iwasawa d'ordre 16
	$C_{4}\rtimes C_{4}$			C4 ⋊ C4
	El grup generat per les matrius de Pauli			grup generat per les matrius de Pauli
	G_4,4 = $C_{2}^{2}\rtimes C_{4}$			C2^2 ⋊ C4

Llibreria de grups petits[modifica]

Els sistemes computacionals algebraics de teoria de grups GAP i Magma contenen la «Llibreria de grups petits» que proporciona accés a descripcions de grups d'ordre baix. Es llisten els grups llevat d'isomorfisme. Actualment^[Quan?] aquesta llibreria conté els grups següents:^[2]

Tots els grups d'ordre com a molt 2000, excepte en l'ordre 1024. Són 423.164.062 grups. Els d'ordre 1024 no apareixen: només comptant els 2-grups d'ordre 1024 no isomorfs n'hi ha 49.487.365.422.
Els d'un ordre lliure de cubs i com a molt 50.000. Són 395.703 grups.
Els d'un ordre lliure de quadrats.
Els d'ordre pⁿ per a n fins a 6 i p un nombre primer.
Els d'ordre p⁷ per a p essent 3, 5, 7 o 11. Són 907.489 grups.
Els d'ordre qⁿ⋅p on qⁿ divideix 2⁸, 3⁶, 5⁵ o 7⁴ i el nombre p és un primer arbitrari diferent de q.
Aquells l'ordre dels quals factoritza en tres primer com a molt.

Conté descripcions explícites dels grups disponibles en format ordinador.

Vegeu també[modifica]

Enllaços externs[modifica]

Pedersen, John. «Groups of small order» (en anglès).
Besche, Hans Ulrich; Eick, Bettina; O'Brien, Eamonn. «The Small Groups library» (en anglès).
Hall, Jr., Marshall; Senior, James K. The Groups of Order 2ⁿ (n ≤ 6) (en anglès). Macmillan, 1964. «Un catàleg exhaustiu dels 340 grups amb ordre divisor de 64.»

Referències[modifica]

↑ Wild, Marcel «The Groups of Order Sixteen Made Easy» (en anglès). American Mathematical Monthly, Gener 2005. Arxivat de l'original el 23 de setembre 2006 [Consulta: 14 febrer 2010]. Arxivat 23 de setembre 2006 a Wayback Machine.
↑ Besche, Hans Ulrich; Eick, Bettina; O'Brien, Eamonn. «The Small Groups library» (en anglès). [Consulta: 14 febrer 2010].

[1] Wild, Marcel «The Groups of Order Sixteen Made Easy» (en anglès). American Mathematical Monthly, Gener 2005. Arxivat de l'original el 23 de setembre 2006 [Consulta: 14 febrer 2010]. Arxivat 23 de setembre 2006 a Wayback Machine.

[2] Besche, Hans Ulrich; Eick, Bettina; O'Brien, Eamonn. «The Small Groups library» (en anglès). [Consulta: 14 febrer 2010].

[1]

[2]