Llista de moments d'inèrcia d'àrees
Aparença
El que segueix és una llista de moments d'inèrcia d'àrees. El moment d'inèrcia d'àrea o el moment de segon ordre té una unitat de dimensió 4 de la longitud (normalment cm4), i no s'ha de confondre amb el moment d'inèrcia de massa, tot i que si la peça és prima, el moment d'inèrcia de massa és igual a la densitat superficial multiplicada pel moment d'inèrcia d'àrea. Tots són respecte a un eix horitzontal que passa a través del centroide de la forma donada, excepte que s'especifiqui quelcom diferent.
| Descripció | Figura | Moment d'inèrcia d'àrea | Comentari | Referència |
|---|---|---|---|---|
| una àrea circular plena de radi r |  |
[1] | ||
| una corona circular de diàmetre interior d1 i diàmetre exterior d₂ | 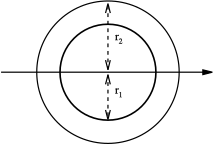 |
Per tubs prims, això equival aproximadament a: o . | ||
| un sector circular ple d'angle θ en radians i radi r respecte un eix que passa pel centroide del sector i pel centre del cercle |  |
|||
| un semicercle ple amb radi r respecte a una línia horitzontal que passa pel centroide de l'àrea |  |
[2] | ||
| un semicercle ple com el de sobre però respecte amb un eix superposat a la base |  |
Això és conseqüència del teorema dels eixos paral·lels i pel fet que la distància entre els dos eixos és | [2] | |
| un semicercle ple com el de sobre però respecte a un eix vertical que passa pel centroide |  |
[2] | ||
| un quart de cercle ple de radi r en el primer quadrant del sistema de coordenades cartesianes |  |
[3] | ||
| un quart de cercle ple com el de sobre però respecte a un eix horitzontal o vertical que passa pel centroide |  |
Això és conseqüència del teorema dels eixos paral·lels i pel fet que la distància entre els dos eixos és | [3] | |
| un el·lipse ple el radi del qual, en l'eix x, és a i, en l'eix y, és b |  | |||
| un rectangle ple la base del qual és b i l'alçada és h |  |
[4] | ||
| un rectangle ple com el de sobre però respecte a un eix superposat a la base |  |
Això és conseqüència del teorema dels eixos paral·lels | [4] | |
| un triangle ple la base del qual és b i l'alçada h respecte a un eix que passa pel centroide |  |
[5] | ||
| un triangle ple com el de sobre però amb un eix superposat a la base |  |
Això és conseqüència del teorema dels eixos paral·lels | [5] | |
| un hexàgon regular ple de costat a |  |
Aquest resultat és vàlid per eixos tant verticals com horitzontals que passin pel centroide i, per tant, també és vàlid per qualsevol eix de direcció arbitrària que passi per l'origen |
Referències
[modifica]- ↑ «Circle». eFunda. [Consulta: 30 desembre 2006].
- ↑ 2,0 2,1 2,2 «Circular Half». eFunda. [Consulta: 30 desembre 2006].
- ↑ 3,0 3,1 «Quarter Circle». eFunda. [Consulta: 30 desembre 2006].
- ↑ 4,0 4,1 «Rectangular area». eFunda. [Consulta: 30 desembre 2006].
- ↑ 5,0 5,1 «Triangular area». eFunda. [Consulta: 30 desembre 2006].

















