Punt de sella
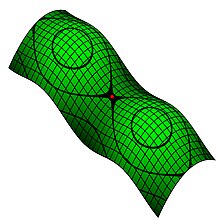
En matemàtiques, un punt de sella o punt d'enselladura és el punt sobre una superfície en què el pendent és zero, però no es tracta d'un extrem local (màxim o mínim). El nom prové de la semblança amb una sella de muntar de les superfícies al voltant d'un punt de sella.[1]
Definició[modifica]
Es defineix com un punt d'una funció en què la primera derivada és nul·la, mentre que el signe de la segona derivada (curvatura) depèn de la direcció en què es calculi. Si en un punt d'una funció de dues variables f (x, y) el gradient és zero, només pot tractar-se d'un màxim, un mínim o un punt de sella .
Propietats[modifica]
D'acord amb la seva definició, el punt d'ensilladura és el més elevat que permet connectar els dos dominis alts adjacents i és també el pas més baix que comunica els dos dominis adjacents que queden per sota. Una altra propietat d'aquests punts és que per ells passa la corba de nivell més profunda que connecta dos dominis elevats, que determina l'elevació a la qual cal descendir per caminar d'una muntanya a una altra. Per un punt d'ensilladura passa també el camí més baix que creua entre dos màxims de la superfície (dues muntanyes).
Rellevància[modifica]
En descriure el relleu terrestre s'usen dos termes equivalents: coll de muntanya i llindar submarí. Un exemple és el Llindar de Camarinal, que separa l'oceà Atlàntic de l'Mar Mediterrani. Per definició, els llacs tenen el seu desguàs en un punt de sella de la topografía.
Exemple[modifica]

Un exemple típic és el Paraboloide hiperbòlic, la funció en :
- .
Per determinar els seus extrems relatius, calculem la seva derivada parcial respecte a x :
al punt on aquesta derivada valgui zero, pot ser un extrem relatiu:
al punt x = 0 pot haver un extrem relatiu, calculant la seva derivada segona veiem:
que és positiva, és a dir, indica un mínim: seguint l'eix de les x , al punt x = 0 la funció presenta un mínim relatiu.
Vegem això mateix en la direcció de l'eix de les y , la seva derivada parcial primera és:
Quan aquesta derivada primera valgui zero, pot presentar un extrem relatiu:
al punt y = 0 , es dona aquesta circumstància, si veiem el seu derivada segona tenim:
que pren valor negatiu, després aquest punt y = 0 , és un màxim relatiu, el punt x = 0 , y = 0 , és un punt de sella, atès que en la direcció de les x és mínim i en la direcció de les y és un màxim.
Vegeu també[modifica]
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Punt de sella |
- Apunts d'anàlisi matemàtica Arxivat 2009-07-22 a Wayback Machine.
Nota[modifica]
- ↑ Tema 5? Extrems de funcions de diversers variables[Enllaç no actiu], Matemàtiques II, Universitat Politècnica de Catalunya,








