Nefroide

La nefroide és la corba vermella

La nefroide és una corba plana el nom de la qual significa forma de ronyons (vegeu nefrologia). Encara que el terme nefroide es feia servir per descriure altres corbes, es va aplicar a la corba d'aquest article per Proctor el 1878. Això i la informació següent es poden verificar a Lockwood, pàg. 62-71 (vegeu Referències).

Equacions de la nefroide

Equacions paramètriques

Les equacions paramètriques de la nefroide mostrada a dalt, amb cúspides a l'eix y, venen donades per

$x=a(3\cos t-\cos 3t),\quad y=a(3\sin t-\sin 3t).$

Quan les cúspides són a l'eix x, les equacions paramètriques venen donades per

$x=a(3\cos t+\cos 3t),\quad y=a(3\sin t+\sin 3t).$

Equació cartesiana

Una equació cartesiana per al nefroide és

$(x^{2}+y^{2}-4a^{2})^{3}=108a^{4}y^{2}$

Propietats de la nefroide

Nefroide càustica al fons d'una tassa de cafè buida.

Nota: Totes les propietats es refereixen a la nefroide parameteritzada pel primer parell d'equacions de dalt.

La longitud de l'arc i l'àrea de la nefroide són, respectivament

$L=24a,\quad A=12\pi a^{2}.$

El radi de curvatura ve donat per

$\rho =|3a\cos t|\,$.

La nefroide com...

... una càustica d'una circumferència

Nefroide com càustica d'una circumferència.

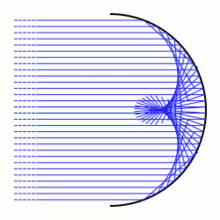
Una nefroide es pot veure com a càustica d'una circumferència per a raigs paral·lels. En altres paraules, si una circumferència reflecteix raigs de llum paral·lels, l'envolupant dels raigs reflectits defineixen una nefroide. Els raigs reflectits es mostren en blau a la figura.

Aquesta propietat reflexiva explica per què la llum brillant produeix un reflex que forma una nefroide en el fons d'una tassa de cafè.

... una evolupant de circumferències

Nefroide com elolupant de circumferències

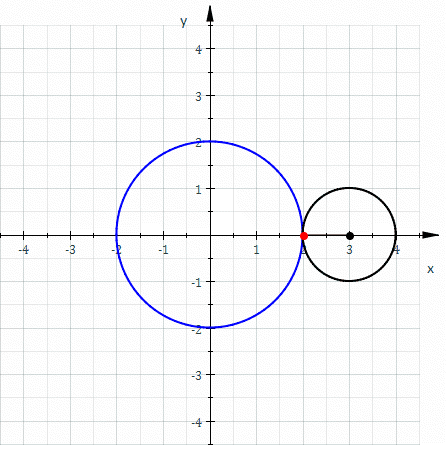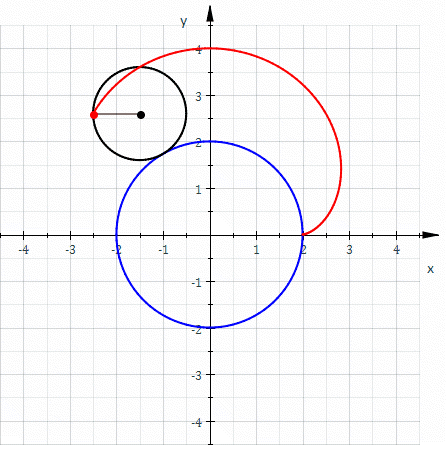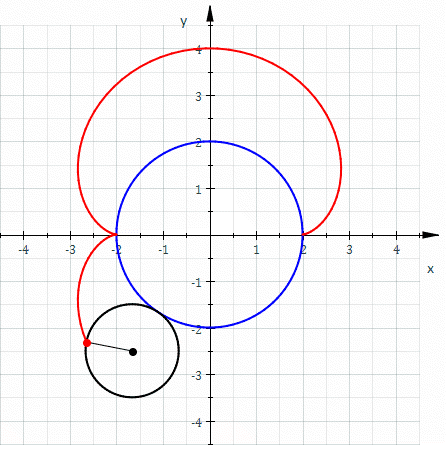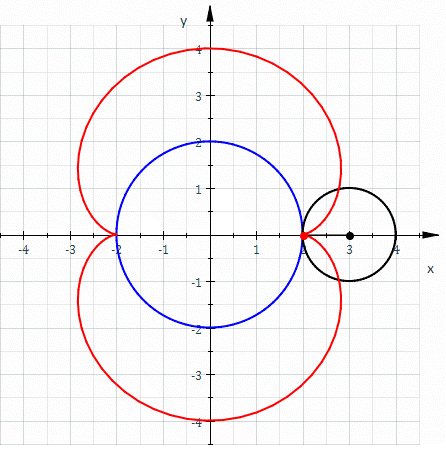
Una nefroide es pot crear com a evolupant de circumferències. Es comença amb un circumferència base (blava), llavors se selecciona un punt en aquest circumferència (punt vermell). Amb aquest punt com centre, es dibuixa una circumferència (vermella) tangent a l'eix d'ordenades. Quan es dibuixen uns quantes circumferències d'aquestes, es produeix la imatge d'una nefroide.

Nefroide com evolupant de rectes

Nota: A la figura, hi ha 36 circumferències els centres de les quals s'espaien 10 graus en el circumferència base.

... una evolupant de rectes

Una nefroide es pot crear com a evolupant de rectes. Es comença amb una circumferència de radi a. Per a diversos valors de t s'uneixen els punts que són a t graus i a 3t graus al voltant d'aquesta circumferència. En altres paraules, s'uneixen els punts $(a\cos t,a\sin t)$ i $(a\cos 3t,a\sin 3t).$ Aquestes rectes evolupen una nefroide.

Nota: En la figura, hi ha 90 rectes que corresponen a prendre el paràmetre t amb valors que són múltiples de 4.

Nefroide com hipocicloide de dues cúspides

... una epicicloide de dues cúspides

La nefroide és també una epicicloide de dues cúspides. En la figura de la part superior de l'article, la circumferència negra petita de radi a és externament tangent a circumferència blava més gran de radi 2a. A mesura que la circumferència més petita rodola al voltant de la circumferència més gran sense lliscar, el punt vermell dibuixa una nefroide.

La figura d'aquest apartat mostra la nefroide com a epicicloide d'una altra manera. La circumferència negra gran de radi 3a és internament tangent a circumferència blava més petita de radi 2a. A mesura le circumferència més gran rodola al voltant de la circumferència més petita sense lliscar, el punt vermell dibuixa una nefroide.

... de la nefroide

L'evoluta...

Evoluta de la nefroide.

L'evoluta de la nefroide és una altra nefroide de mida meitat i girada 90 graus. La nefroide original és visible com evolupant de les seves circumferències osculadores (gris). es mostren dues circumferències osculadores (blau). Els centres d'aquestes circumferències es veu que romanen sobre l'evoluta (nefroide més petita, vermell).

Nota: En la figura, hi ha 60 circumferències que corresponen a prendre pel paràmetre t valors que són múltiples de 6.

La involuta...

Com que l'evoluta del nefroide és una altra nefroide, així la involuta de la nefroide és també una altra nefroide. La nefroide original (evolupant de les circumferències grises) en la imatge prèvia és la involuta de la nefroide vermella més petita.

La inversa...

Inversa de la nefroide

La inversa respecte a l'origen de la nefroide (vermell) és la corba mostrada com a evolupant de circumferències (negre). Aquests circumferències són inverses a aquelles de la figura de dalt que descriu la nefroide com a evolupant de circumferències.

Invertint-la respecte a una circumferència de radi a l'equació cartesiana de la inversa és

$(a^{2}-4(x^{2}+y^{2}))^{3}=108a^{2}x^{2}(x^{2}+y^{2}).$

Bibliografia

• Lockwood, E. H., A Book of Curves, Cambridge University Press, 1961.
• Wells D. The Penguin Dictionary of Curious and Interesting Geometry. Nova York: Penguin Books, 1991, p. 158. ISBN 0-14-011813-6. 

Enllaços externs

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Nefroide

• Weisstein, Eric W., «Nephroid» a MathWorld (en anglès).