Càrrega elèctrica
 | |
| Símbol | q i Q |
|---|---|
| Unitats | coulomb i ampere second (en) |
| Fórmula | |
La càrrega elèctrica[1] (habitualment representada com Q) és una propietat fonamental associada a les partícules subatòmiques que segueix la llei de conservació i determina el seu comportament davant les interaccions electromagnètiques. La matèria elèctricament carregada és influenciada pels camps electromagnètics i, al seu torn, també produeix camps electromagnètics. La interacció entre una càrrega en moviment i un camp electromagnètic és l'origen de la força electromagnètica que és una de les quatre forces fonamentals de la natura.
Totes les partícules conegudes tenen càrregues elèctriques que són múltiples enters de la càrrega de l'electró e; la càrrega elèctrica s'expressa quantitzada com un múltiple de la càrrega elemental e. Per exemple, els protons tenen càrrega +e, i els neutrons tenen càrrega zero (són elèctricament neutres).[2] La sola excepció són els quarks, que tenen càrregues fraccionàries de e/3 i 2e/3; tanmateix, els quarks mai es presenten sols a la natura, sinó formant combinacions de càrrega entera. Les antipartícules tenen càrregues elèctriques de signe oposat respecte de la seva corresponent partícula.
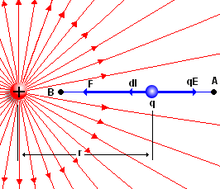
Clàssicament, donades dues partícules en repòs amb càrregues q i q' , separades una distància r, aquestes s'atreuen mútuament amb una força F que ve donada per la llei de Coulomb, que estableix que la força d'atracció o repulsió és directament proporcional a la magnitud de les càrregues i inversament proporcional al quadrat de la distància que les separa.
on és la permitivitat del buit.
La càrrega elèctrica pot ser negativa o positiva. Dues càrregues d'igual signe es repel·leixen, i dues càrregues de signe oposat s'atreuen. Per convenció, hom considera que l'electró té càrrega negativa, i el valor absolut de la seva càrrega s'acostuma a denotar e.
La càrrega elèctrica dels objectes macroscòpics és la suma de la càrrega elèctrica del conjunt de les seves partícules. habitualment la càrrega elèctrica és nul·la, atès que a cada àtom el nombre d'electrons és igual al nombre de protons i, per tant les càrregues respectives s'anul·len. Moltes vegades la presència d'una càrrega elèctrica neta està relacionada amb l'electricitat estàtica. A més la càrrega pot no presentar una distribució uniforme (a causa d'un camp elèctric extern, per exemple), fins i tot en els casos en què la càrrega elèctrica neta sigui zero, i llavors es parla de polarització elèctrica. Un moviment ordenat de partícules carregades cap a una direcció particular (als metalls serien els electrons) és el que es coneix com a corrent elèctric. La natura discreta de la càrrega elèctrica va ser proposada per Michael Faraday a partir de les seves observacions experimentals de l'electròlisi, però no va ser demostrada fins que Robert Millikan va fer el seu experiment de la gota d'oli.
En el sistema internacional la unitat de càrrega elèctrica és el coulomb (C). En física de partícules la càrrega del electró e és una unitat de càrrega habitual. Aproximadament, 1 C = 6,24 x 1018 càrregues elementals. El coulomb es defineix com la quantitat de càrrega elèctrica total que passa per una secció transversal d'un conductor pel qual circula un corrent elèctric d'un ampere durant un segon.
La quantitat de càrrega elèctrica es pot mesurar directament amb un electroscopi o indirectament amb un galvanòmetre
Vegeu també
[modifica]- Braçalet antiestàtic
- Densitat de corrent
- Descàrrega electroestàtica
- Electricitat estàtica
- Electroestàtica
- Generador electroestàtic
- Influència total
- Unitats electromagnètiques
Referències
[modifica]- ↑ «Càrrega elèctrica». Gran Enciclopèdia Catalana. Barcelona: Grup Enciclopèdia Catalana.
- ↑ «Càrrega elèctrica». Gran Enciclopèdia Catalana. Barcelona: Grup Enciclopèdia Catalana.



